函数的极限2
图片预览





文档简介
课件14张PPT。2.3 函数的极限(2)一、复习引入:
无穷极限的定义: 如果 =a,且 =a, 那么就说当 x 趋向于
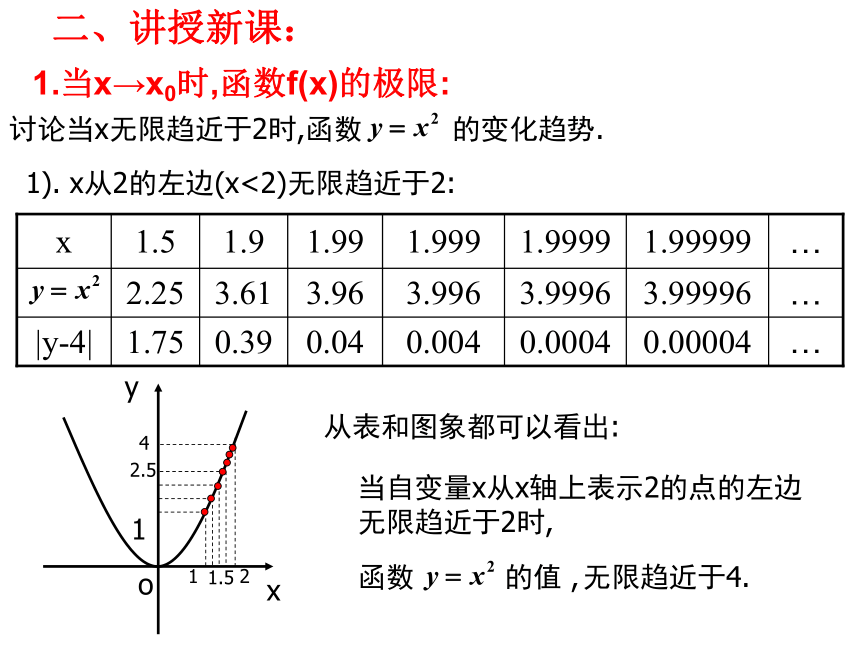
无穷大时, 的极限是a,记作 可否用类似的思想和方法研究x→x0时的函数极限?xy111.52.524讨论当x无限趋近于2时,函数 的变化趋势.1). x从2的左边(x<2)无限趋近于2:…0.000040.00040.0040.040.391.75|y-4|…3.999963.99963.9963.963.612.25…1.999991.99991.9991.991.91.5x从表和图象都可以看出:当自变量x从x轴上表示2的点的左边
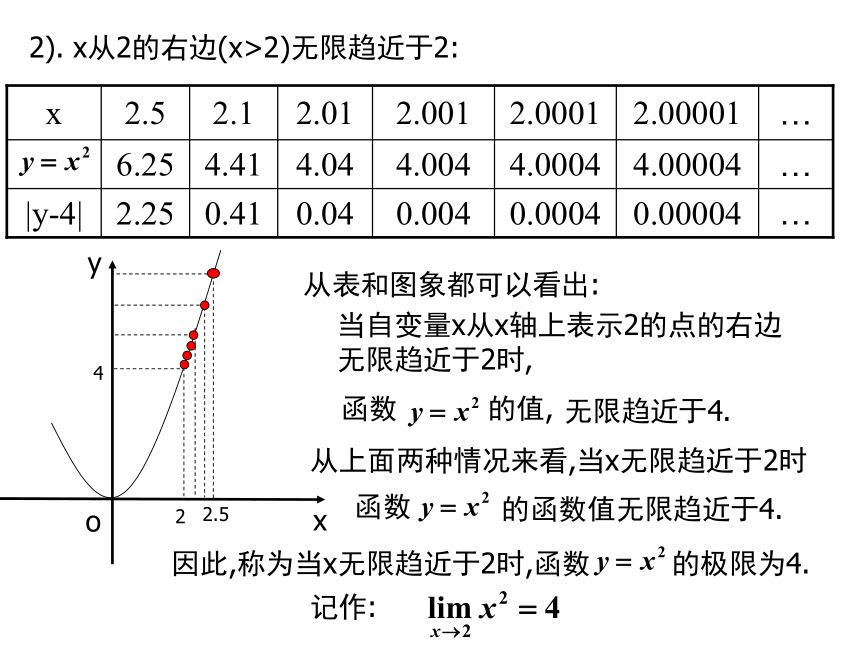
无限趋近于2时,o二、讲授新课:1.当x→x0时,函数f(x)的极限:xy242). x从2的右边(x>2)无限趋近于2:…0.000040.00040.0040.040.412.25|y-4|…4.000044.00044.0044.044.416.25…2.000012.00012.0012.012.12.5x从表和图象都可以看出:当自变量x从x轴上表示2的点的右边
无限趋近于2时,2.5从上面两种情况来看,当x无限趋近于2时因此,称为当x无限趋近于2时,函数 的极限为4.记作:o再讨论当x无限趋近于1(但不等于1)时,函数 的变化趋势.所以,当x无限趋近于1(但不等于1)时,y的值无限趋近于2.记作:定义:当自变量x无限趋近于常数 (但不等于 )时,如果函数无限趋近于一个常数就说当x趋近于时,函数 的极限是记作:也可记作:也叫做函数在点处的极限.例1、当 时,写出下列函数的极限:解:(4)y=5是常数函数,函数值始终等于常数5.有函数极限的
定义,容易得到一般地,设C为常数,则例2、写出下列极限的值:5011471)从表示 的点的左边无限趋近于 ;2)从表示 的点的右边无限趋近于 ;3)从表示 的点的两侧交错地无限趋近于 ;总之,不管以哪种方式趋近,2.函数的左右极限:x当x从原点O的左侧无限趋近于0时,函数无限趋近于-1;当x从原点O的右侧无限趋近于0时,函数无限趋近于1.由于x从不同方向无限趋近于0时,所无限趋近的值不同,所以,在x=0处无极限.即考虑到函数但是,如果限制x只能从原点O的某一侧无限趋近于0,函数就会无限趋近于一个确定的常数.比如:由此,我们得到单侧极限的定义.一般地,如果当x从点 左侧(即 )无限趋近于 时,函数无限趋近于常数就说 是函数记作在点处的左极限,一般地,如果当x从点 右侧(即 )无限趋近于 时,函数无限趋近于常数就说 是函数记作在点处的右极限,由函数在一点处的左、右极限定义可知,对于函数根据函数在一点处的极限、左极限和右极限的定义,可以得出
无穷极限的定义: 如果 =a,且 =a, 那么就说当 x 趋向于
无穷大时, 的极限是a,记作 可否用类似的思想和方法研究x→x0时的函数极限?xy111.52.524讨论当x无限趋近于2时,函数 的变化趋势.1). x从2的左边(x<2)无限趋近于2:…0.000040.00040.0040.040.391.75|y-4|…3.999963.99963.9963.963.612.25…1.999991.99991.9991.991.91.5x从表和图象都可以看出:当自变量x从x轴上表示2的点的左边
无限趋近于2时,o二、讲授新课:1.当x→x0时,函数f(x)的极限:xy242). x从2的右边(x>2)无限趋近于2:…0.000040.00040.0040.040.412.25|y-4|…4.000044.00044.0044.044.416.25…2.000012.00012.0012.012.12.5x从表和图象都可以看出:当自变量x从x轴上表示2的点的右边
无限趋近于2时,2.5从上面两种情况来看,当x无限趋近于2时因此,称为当x无限趋近于2时,函数 的极限为4.记作:o再讨论当x无限趋近于1(但不等于1)时,函数 的变化趋势.所以,当x无限趋近于1(但不等于1)时,y的值无限趋近于2.记作:定义:当自变量x无限趋近于常数 (但不等于 )时,如果函数无限趋近于一个常数就说当x趋近于时,函数 的极限是记作:也可记作:也叫做函数在点处的极限.例1、当 时,写出下列函数的极限:解:(4)y=5是常数函数,函数值始终等于常数5.有函数极限的
定义,容易得到一般地,设C为常数,则例2、写出下列极限的值:5011471)从表示 的点的左边无限趋近于 ;2)从表示 的点的右边无限趋近于 ;3)从表示 的点的两侧交错地无限趋近于 ;总之,不管以哪种方式趋近,2.函数的左右极限:x当x从原点O的左侧无限趋近于0时,函数无限趋近于-1;当x从原点O的右侧无限趋近于0时,函数无限趋近于1.由于x从不同方向无限趋近于0时,所无限趋近的值不同,所以,在x=0处无极限.即考虑到函数但是,如果限制x只能从原点O的某一侧无限趋近于0,函数就会无限趋近于一个确定的常数.比如:由此,我们得到单侧极限的定义.一般地,如果当x从点 左侧(即 )无限趋近于 时,函数无限趋近于常数就说 是函数记作在点处的左极限,一般地,如果当x从点 右侧(即 )无限趋近于 时,函数无限趋近于常数就说 是函数记作在点处的右极限,由函数在一点处的左、右极限定义可知,对于函数根据函数在一点处的极限、左极限和右极限的定义,可以得出
