浙江义乌市第二中学 函数的极限[上学期]
文档属性
| 名称 | 浙江义乌市第二中学 函数的极限[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 206.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-16 00:00:00 | ||
图片预览




文档简介
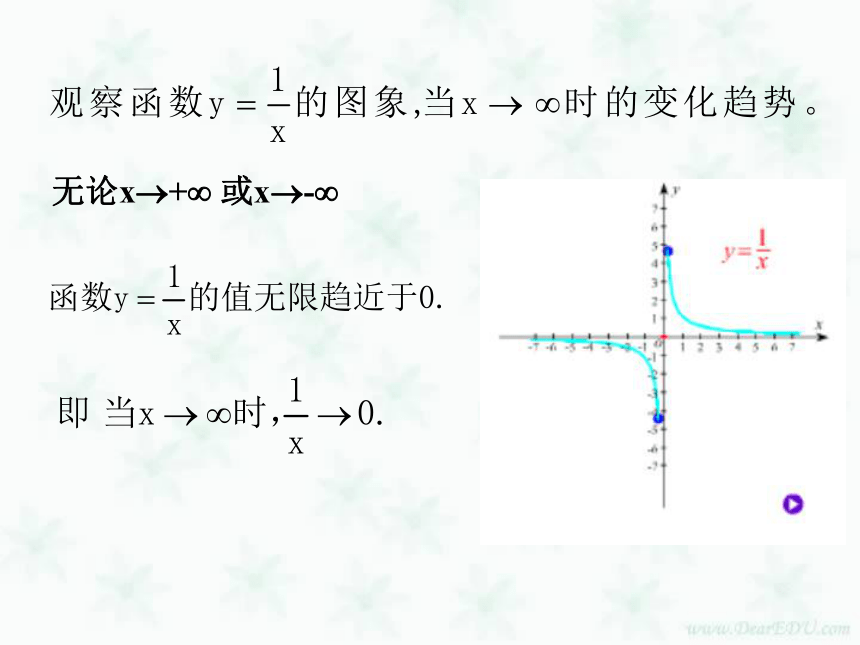
课件15张PPT。复习1、数列的极限:如果当项数n 无限增大,数列的项 an无限趋近于某个常数a(即 | an - a | 无限地接近于0),称数列{an} 以a为极限。数列{an} 以a为极限,记作2、常见数列的极限 如:③ 当|a|<1时,则①②3、数列与函数的关系:数列可以看作是定义在正整数集上的一种特殊函数。函数的极限(一)无论x?+? 或x?-? 2.3 函数的极限 当自变量x 取正值并无限增
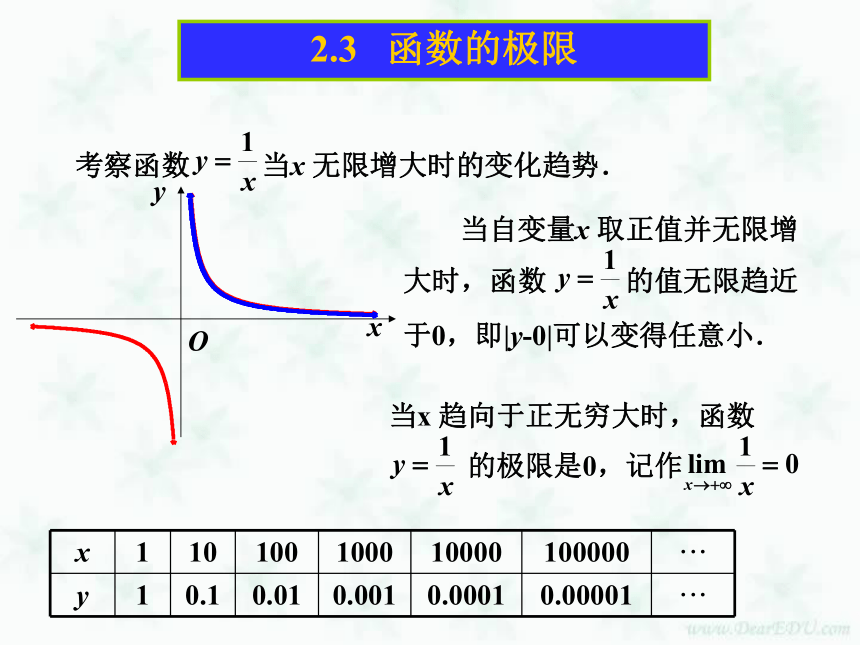
大时,函数 的值无限趋近
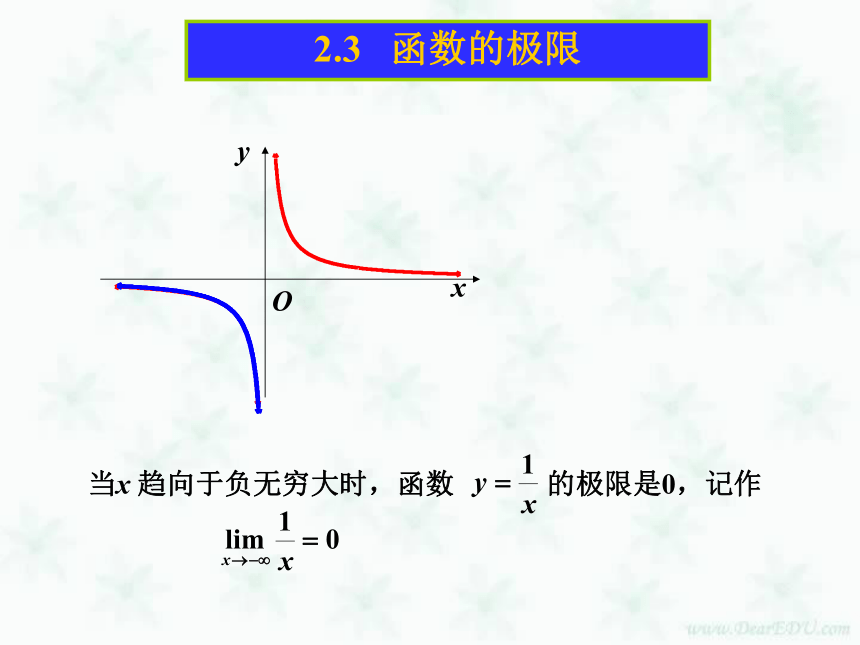
于0,即|y-0|可以变得任意小.2.3 函数的极限2.3 函数的极限2.3 函数的极限2.3 函数的极限2.3 函数的极限当 时, 趋近于2.3 函数的极限(2)当 时, 无限趋近于0,即2.3 函数的极限(3)解:当 时, 的值保持为1.即当 时, 的值保持为-1,即解 函数图象如右图所示,由图象可以看出:例2、观察函数 的图象,写出极限课 堂 练 习1.观察函数y=ex的图象,并写出2.下列函数当x?? 时极限是否存在,试说明理由,并画图观察。(2) f(x)=1BD2.3 函数的极限课堂小结 本节学习了当x分别趋向于+∞,-∞,∞时,函数f(x)的极限,以及常数函数的极限,并且注意 中的∞和数列极限 中的∞不同意义,以概念为依据,结合函数图象,学会求一些函数的极限。
大时,函数 的值无限趋近
于0,即|y-0|可以变得任意小.2.3 函数的极限2.3 函数的极限2.3 函数的极限2.3 函数的极限2.3 函数的极限当 时, 趋近于2.3 函数的极限(2)当 时, 无限趋近于0,即2.3 函数的极限(3)解:当 时, 的值保持为1.即当 时, 的值保持为-1,即解 函数图象如右图所示,由图象可以看出:例2、观察函数 的图象,写出极限课 堂 练 习1.观察函数y=ex的图象,并写出2.下列函数当x?? 时极限是否存在,试说明理由,并画图观察。(2) f(x)=1BD2.3 函数的极限课堂小结 本节学习了当x分别趋向于+∞,-∞,∞时,函数f(x)的极限,以及常数函数的极限,并且注意 中的∞和数列极限 中的∞不同意义,以概念为依据,结合函数图象,学会求一些函数的极限。
