人教版九年级数学上册22.3.3拱桥问题和运动中的抛物线 一课一练 (含答案)
文档属性
| 名称 | 人教版九年级数学上册22.3.3拱桥问题和运动中的抛物线 一课一练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 67.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-30 15:46:43 | ||
图片预览


文档简介
人教版 九年级数学上册一课一练
22.3.3 拱桥问题和运动中的抛物线
一.选择题
1.一足球被踢出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=-(t-2)2+5,则当足球距离地面的高度最大时,飞行时间为( )
A.2秒 B.3秒 C.4秒 D.5秒
2. 如图,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=-(x-2)2+6,则水柱的最大高度是( )
A. 2 B. 4 C. 6 D. 2+
3. 已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( )
A. y=x2-2x+2 B. y=x2-2x-2
C. y=-x2-2x+1 D. y=x2-2x+1,
4. 对于抛物线y=x2-2x-1,下列说法正确的是( )
A. 对称轴是直线x=-1
B. 顶点坐标为(1,-2)
C. 与x轴交于(0,-1)
D. 当x=1时,y有最小值2
5.某店加工烤鸡时,烤鸡的口感系数y和加工时间t(h)之间的关系式为y=-0.2t2+1.4t-2,口感系数越大,口感越好,则最佳加工时间为( )
A.3 B.3或4 C.3.5 D.3或5
二.填空题
1.九年级某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图的抛物线y=-x2+x+的一部分,则该同学的成绩是 m.
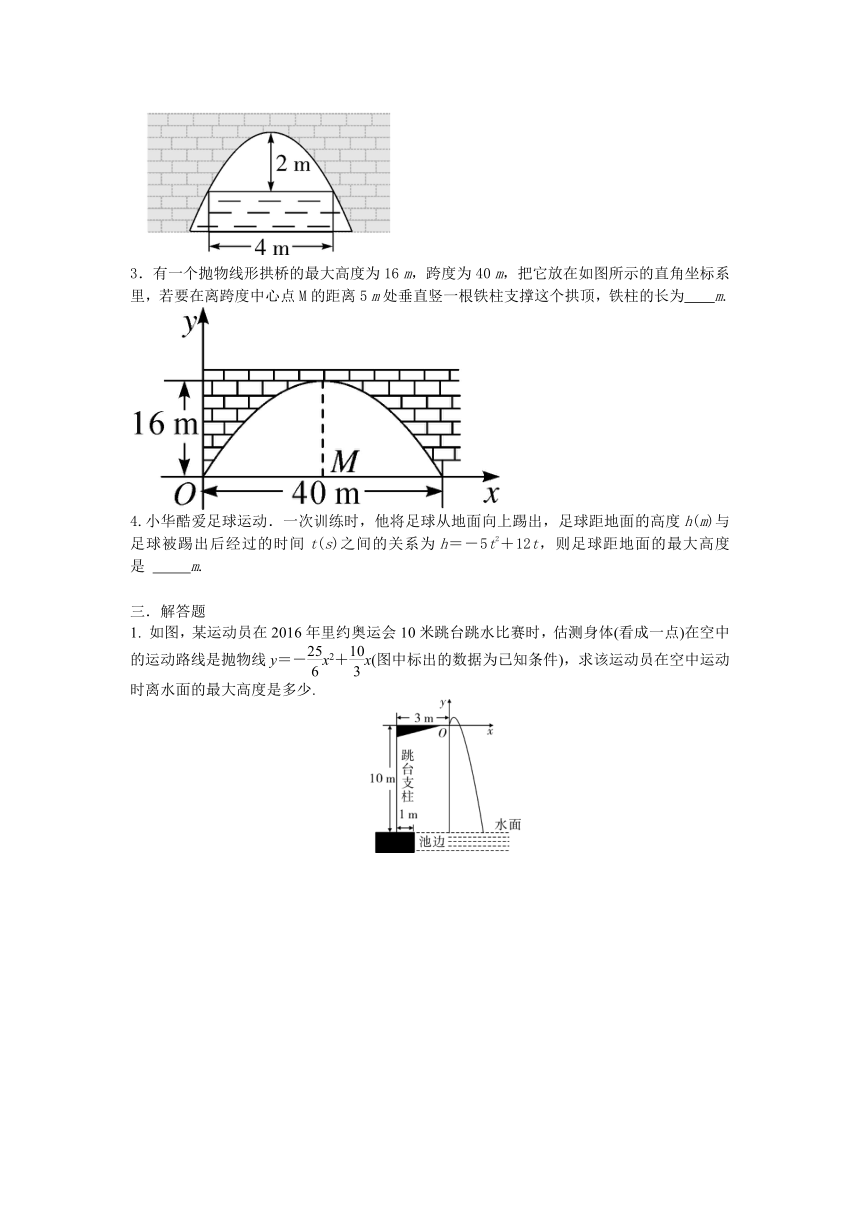
2.如图,一抛物线形拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m,那么当水位下降2 m后,水面的宽度增加 m.
3.有一个抛物线形拱桥的最大高度为16 m,跨度为40 m,把它放在如图所示的直角坐标系里,若要在离跨度中心点M的距离5 m处垂直竖一根铁柱支撑这个拱顶,铁柱的长为 m.
4.小华酷爱足球运动.一次训练时,他将足球从地面向上踢出,足球距地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系为h=-5t2+12t,则足球距地面的最大高度 是 m.
三.解答题
1. 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),求该运动员在空中运动时离水面的最大高度是多少.
2.. 要在一个圆形广场中央修建一个音乐喷泉,在广场中央竖直安装一根水管. 在水管的顶点安一个喷水头,使喷出的抛物线水柱在与广场中央的水平距离为1 m处达到最高,且最高为3 m,水柱落地处离广场中央3 m,建立如图的直角坐标系.
(1)求抛物线的解析式;
(2)求水管的长度.
3. 一座隧道的截面由抛物线和长方形组成,长方形的长为8 m,宽为2 m,隧道的最高点P位于AB的中央且距地面6 m,建立如图的坐标系.
(1)求抛物线的解析式;
(2)一辆货车高4 m,宽2 m,通过计算说明其能否从该隧道内通过;
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过?为什么?
人教版 九年级数学上册一课一练
22.3.3 拱桥问题和运动中的抛物线
参考答案
一.选择题
1.一足球被踢出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=-(t-2)2+5,则当足球距离地面的高度最大时,飞行时间为( A )
A.2秒 B.3秒 C.4秒 D.5秒
2. 如图,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=-(x-2)2+6,则水柱的最大高度是( C )
A. 2 B. 4 C. 6 D. 2+
3. 已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( B )
A. y=x2-2x+2 B. y=x2-2x-2
C. y=-x2-2x+1 D. y=x2-2x+1,
4. 对于抛物线y=x2-2x-1,下列说法正确的是( B )
A. 对称轴是直线x=-1
B. 顶点坐标为(1,-2)
C. 与x轴交于(0,-1)
D. 当x=1时,y有最小值2
5.某店加工烤鸡时,烤鸡的口感系数y和加工时间t(h)之间的关系式为y=-0.2t2+1.4t-2,口感系数越大,口感越好,则最佳加工时间为( C )
A.3 B.3或4 C.3.5 D.3或5
二.填空题
1.九年级某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图的抛物线y=-x2+x+的一部分,则该同学的成绩是 8 m.
2.如图,一抛物线形拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m,那么当水位下降2 m后,水面的宽度增加 (4-4) m.
3.有一个抛物线形拱桥的最大高度为16 m,跨度为40 m,把它放在如图所示的直角坐标系里,若要在离跨度中心点M的距离5 m处垂直竖一根铁柱支撑这个拱顶,铁柱的长为 15 m.
4.小华酷爱足球运动.一次训练时,他将足球从地面向上踢出,足球距地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系为h=-5t2+12t,则足球距地面的最大高度是 7.2 m.
三.解答题
1. 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),求该运动员在空中运动时离水面的最大高度是多少.
解:∵y=-x2+x=-2+,
∴y的最大值为.
∴运动员在空中运动时离水面的最大高度为
10+=10(m).
2.. 要在一个圆形广场中央修建一个音乐喷泉,在广场中央竖直安装一根水管. 在水管的顶点安一个喷水头,使喷出的抛物线水柱在与广场中央的水平距离为1 m处达到最高,且最高为3 m,水柱落地处离广场中央3 m,建立如图的直角坐标系.
(1)求抛物线的解析式;
(2)求水管的长度.
解:(1)设y=a(x-1)2+3.
∵点(3,0)在此抛物线上,
∴0=a(3-1)2+3.
解得a=-,即抛物线的解析式为y=-(x-1)2+3.
(2)当x=0时,y=-(0-1)2+3=2.
答:水管的长度是2 m.
3. 一座隧道的截面由抛物线和长方形组成,长方形的长为8 m,宽为2 m,隧道的最高点P位于AB的中央且距地面6 m,建立如图的坐标系.
(1)求抛物线的解析式;
(2)一辆货车高4 m,宽2 m,通过计算说明其能否从该隧道内通过;
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过?为什么?
解:(1)y=-(x-4)2+6.
(2)由图象可知,当y=4时,x1=4-2,x2=4+2,
∴=4>2.
∴一辆货车高4 m,宽2 m,能从该隧道内通过.
(3)由(2)知,=2>2,
∴这辆货车可以顺利通过.
22.3.3 拱桥问题和运动中的抛物线
一.选择题
1.一足球被踢出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=-(t-2)2+5,则当足球距离地面的高度最大时,飞行时间为( )
A.2秒 B.3秒 C.4秒 D.5秒
2. 如图,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=-(x-2)2+6,则水柱的最大高度是( )
A. 2 B. 4 C. 6 D. 2+
3. 已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( )
A. y=x2-2x+2 B. y=x2-2x-2
C. y=-x2-2x+1 D. y=x2-2x+1,
4. 对于抛物线y=x2-2x-1,下列说法正确的是( )
A. 对称轴是直线x=-1
B. 顶点坐标为(1,-2)
C. 与x轴交于(0,-1)
D. 当x=1时,y有最小值2
5.某店加工烤鸡时,烤鸡的口感系数y和加工时间t(h)之间的关系式为y=-0.2t2+1.4t-2,口感系数越大,口感越好,则最佳加工时间为( )
A.3 B.3或4 C.3.5 D.3或5
二.填空题
1.九年级某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图的抛物线y=-x2+x+的一部分,则该同学的成绩是 m.
2.如图,一抛物线形拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m,那么当水位下降2 m后,水面的宽度增加 m.
3.有一个抛物线形拱桥的最大高度为16 m,跨度为40 m,把它放在如图所示的直角坐标系里,若要在离跨度中心点M的距离5 m处垂直竖一根铁柱支撑这个拱顶,铁柱的长为 m.
4.小华酷爱足球运动.一次训练时,他将足球从地面向上踢出,足球距地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系为h=-5t2+12t,则足球距地面的最大高度 是 m.
三.解答题
1. 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),求该运动员在空中运动时离水面的最大高度是多少.
2.. 要在一个圆形广场中央修建一个音乐喷泉,在广场中央竖直安装一根水管. 在水管的顶点安一个喷水头,使喷出的抛物线水柱在与广场中央的水平距离为1 m处达到最高,且最高为3 m,水柱落地处离广场中央3 m,建立如图的直角坐标系.
(1)求抛物线的解析式;
(2)求水管的长度.
3. 一座隧道的截面由抛物线和长方形组成,长方形的长为8 m,宽为2 m,隧道的最高点P位于AB的中央且距地面6 m,建立如图的坐标系.
(1)求抛物线的解析式;
(2)一辆货车高4 m,宽2 m,通过计算说明其能否从该隧道内通过;
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过?为什么?
人教版 九年级数学上册一课一练
22.3.3 拱桥问题和运动中的抛物线
参考答案
一.选择题
1.一足球被踢出后,距离地面的高度h(米)和飞行时间t(秒)满足下列函数解析式:h=-(t-2)2+5,则当足球距离地面的高度最大时,飞行时间为( A )
A.2秒 B.3秒 C.4秒 D.5秒
2. 如图,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=-(x-2)2+6,则水柱的最大高度是( C )
A. 2 B. 4 C. 6 D. 2+
3. 已知抛物线y=x2+bx+c的顶点坐标为(1,-3),则抛物线对应的函数解析式为( B )
A. y=x2-2x+2 B. y=x2-2x-2
C. y=-x2-2x+1 D. y=x2-2x+1,
4. 对于抛物线y=x2-2x-1,下列说法正确的是( B )
A. 对称轴是直线x=-1
B. 顶点坐标为(1,-2)
C. 与x轴交于(0,-1)
D. 当x=1时,y有最小值2
5.某店加工烤鸡时,烤鸡的口感系数y和加工时间t(h)之间的关系式为y=-0.2t2+1.4t-2,口感系数越大,口感越好,则最佳加工时间为( C )
A.3 B.3或4 C.3.5 D.3或5
二.填空题
1.九年级某班一女生在一次投掷实心球的测试中,实心球所经过的路线为如图的抛物线y=-x2+x+的一部分,则该同学的成绩是 8 m.
2.如图,一抛物线形拱桥,当拱顶到水面的距离为2 m时,水面宽度为4 m,那么当水位下降2 m后,水面的宽度增加 (4-4) m.
3.有一个抛物线形拱桥的最大高度为16 m,跨度为40 m,把它放在如图所示的直角坐标系里,若要在离跨度中心点M的距离5 m处垂直竖一根铁柱支撑这个拱顶,铁柱的长为 15 m.
4.小华酷爱足球运动.一次训练时,他将足球从地面向上踢出,足球距地面的高度h(m)与足球被踢出后经过的时间t(s)之间的关系为h=-5t2+12t,则足球距地面的最大高度是 7.2 m.
三.解答题
1. 如图,某运动员在2016年里约奥运会10米跳台跳水比赛时,估测身体(看成一点)在空中的运动路线是抛物线y=-x2+x(图中标出的数据为已知条件),求该运动员在空中运动时离水面的最大高度是多少.
解:∵y=-x2+x=-2+,
∴y的最大值为.
∴运动员在空中运动时离水面的最大高度为
10+=10(m).
2.. 要在一个圆形广场中央修建一个音乐喷泉,在广场中央竖直安装一根水管. 在水管的顶点安一个喷水头,使喷出的抛物线水柱在与广场中央的水平距离为1 m处达到最高,且最高为3 m,水柱落地处离广场中央3 m,建立如图的直角坐标系.
(1)求抛物线的解析式;
(2)求水管的长度.
解:(1)设y=a(x-1)2+3.
∵点(3,0)在此抛物线上,
∴0=a(3-1)2+3.
解得a=-,即抛物线的解析式为y=-(x-1)2+3.
(2)当x=0时,y=-(0-1)2+3=2.
答:水管的长度是2 m.
3. 一座隧道的截面由抛物线和长方形组成,长方形的长为8 m,宽为2 m,隧道的最高点P位于AB的中央且距地面6 m,建立如图的坐标系.
(1)求抛物线的解析式;
(2)一辆货车高4 m,宽2 m,通过计算说明其能否从该隧道内通过;
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过?为什么?
解:(1)y=-(x-4)2+6.
(2)由图象可知,当y=4时,x1=4-2,x2=4+2,
∴=4>2.
∴一辆货车高4 m,宽2 m,能从该隧道内通过.
(3)由(2)知,=2>2,
∴这辆货车可以顺利通过.
同课章节目录
