28.1.3圆周角 学案
图片预览

文档简介
课 题:《圆周角定理及推论1》
序 号: ( 5 )
年 级: 九年级 单元名称:第28章 圆
课 型: 新授课 上课时间:
学习内容:华东师大版课本 页
学习目标:
1.理解圆周角的概念,
2.掌握圆周角定理及其推论的内容及简单应用;
3.经历探索圆周角定理的过程,体会分类、转化等数学思想方法。
重 点:圆周角的概念和圆周角定理及推论。
难 点:圆周角定理的证明中由“一般到特殊”的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想方法和分类的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想.
学法指导:合作探究
学 习 过 程
自主预习课本 页,完成下列各题:
圆周角的定义
顶点在 ,并且两边都和圆 的角叫做圆周角.
2.判断下列各图中的角是否是圆周角。
及
3.圆周角定理:
1、圆心角的定义: 。
2.圆心角、弧、弦、弦心距关系定理:
在定理中注意不能丢掉 这个前提。
3.什么叫弧?弧分哪几种?
探究:弧与圆心角的关系
问题导学:
1.在一个圆中,任作一个圆心角,它对应的弧有几条吗?
任作一条弧,它对应的圆心角有几个?
如图所示,圆心角对应的是弧AB。
这就说明:弧与圆心角的对应关系是唯一的。
2.当圆心角逐渐增大时,它对应的弧怎样变化?当圆心角减小时,它对应的弧又怎么变化?
这就说明:弧的大小会随着它对应的圆心角的大小而变化。
圆中最大的弧是什么?此时它对应的圆心角是什么?这个圆心角是多少度?
这就说明:整个圆周也是一段弧,它对应的圆心角是个周角,等于360度。
此时,我们就说整个圆周这段弧的度数就是它对应的圆心角的度数,等于360度。
半圆是弧吗?它对应的圆心角等于多少度?
这就说明:半圆这段弧的度数就是它对应的圆心角的度数,等于180度。
如果把圆周四等分,每段弧是多少度呢?六等分呢?10等分呢?n等分呢?
综上,我们得到这样的结论:
弧是有度数的,它的度数等于它所对应的圆心角的度数。
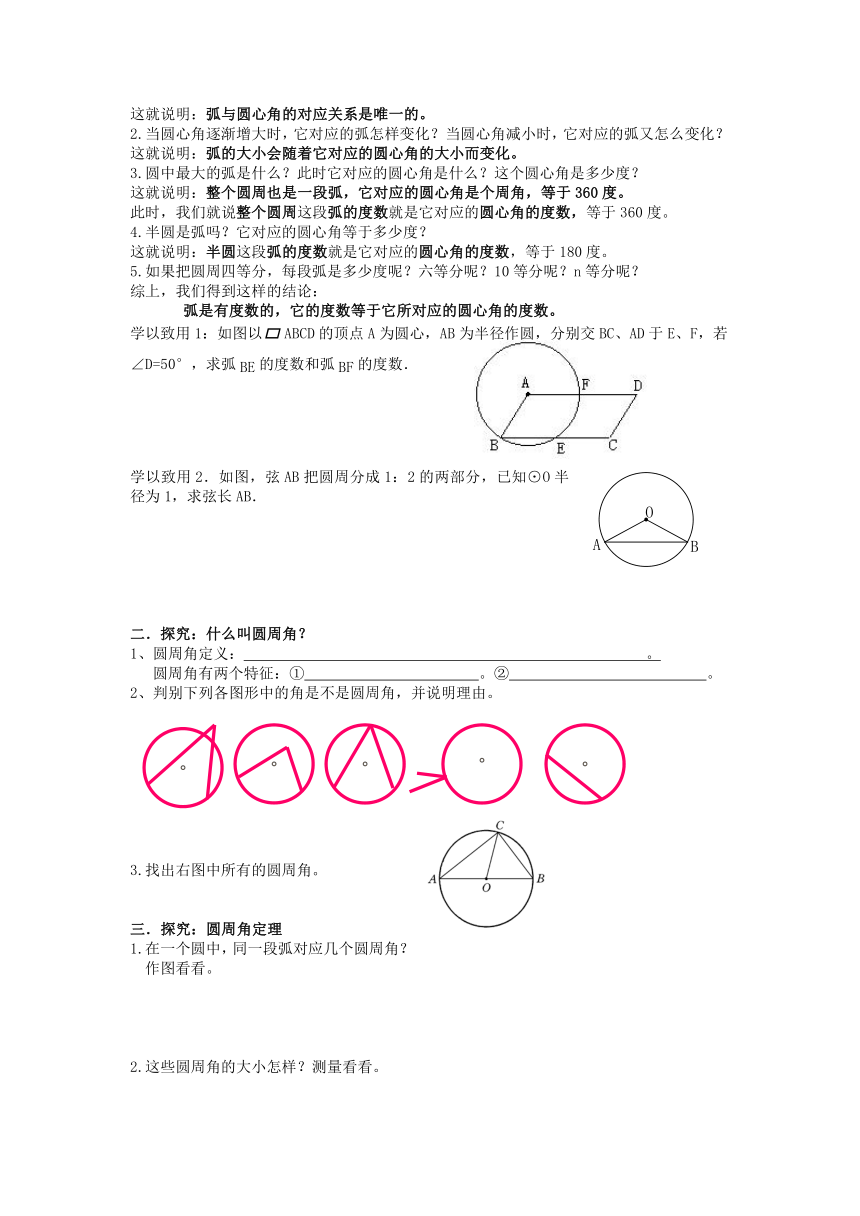
学以致用1:如图以ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若
∠D=50°,求弧BE的度数和弧BF的度数.
学以致用2.如图,弦AB把圆周分成1:2的两部分,已知⊙O半径为1,求弦长AB.
探究:什么叫圆周角?
1、圆周角定义: 。
圆周角有两个特征:① 。② 。
2、判别下列各图形中的角是不是圆周角,并说明理由。
3.找出右图中所有的圆周角。
三.探究:圆周角定理
在一个圆中,同一段弧对应几个圆周角?
作图看看。
这些圆周角的大小怎样?测量看看。
这段弧所对的圆心角有几个?
4.这些圆周角和这个圆心角的大小有什么关系?测量看看。
由上述操作我们可以猜想:
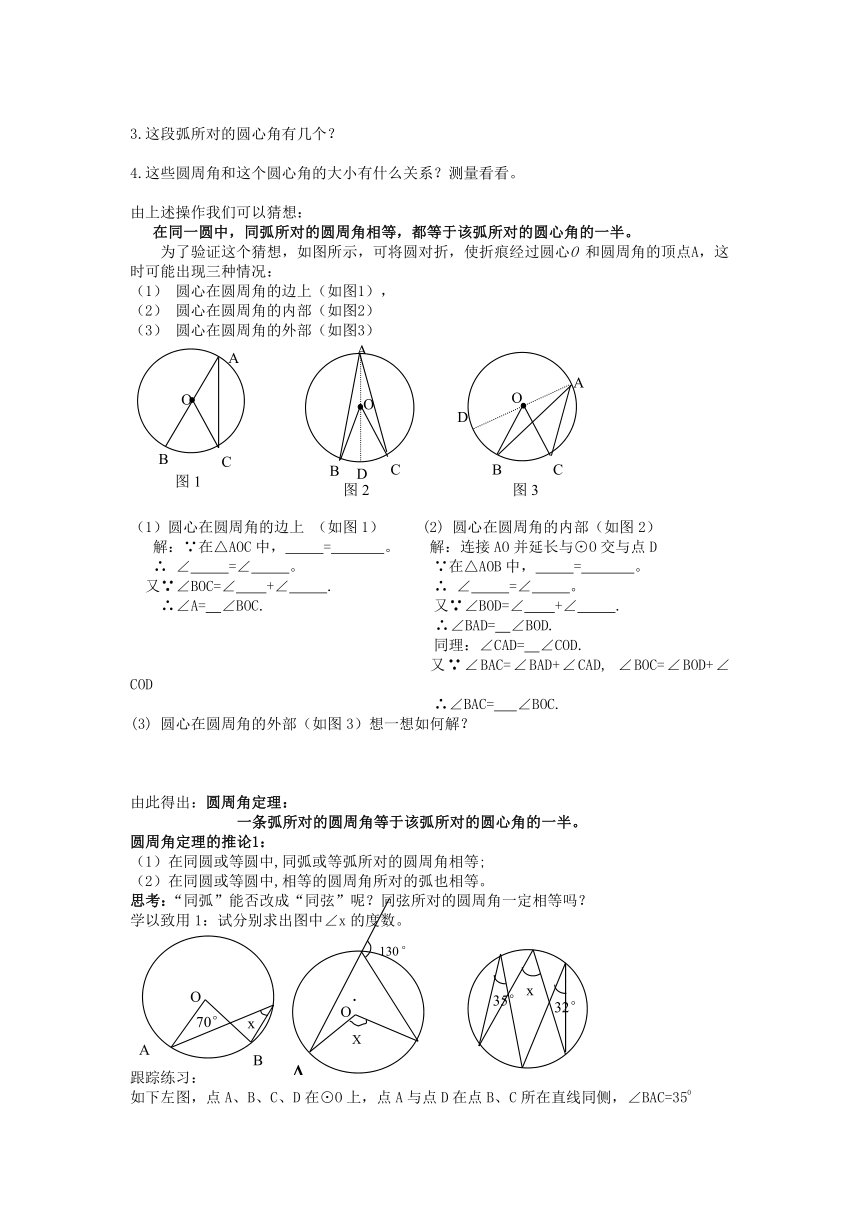
在同一圆中,同弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
为了验证这个猜想,如图所示,可将圆对折,使折痕经过圆心O 和圆周角的顶点A,这时可能出现三种情况:
圆心在圆周角的边上(如图1),
圆心在圆周角的内部(如图2)
(3) 圆心在圆周角的外部(如图3)
(1)圆心在圆周角的边上 (如图1) (2) 圆心在圆周角的内部(如图2)
解:∵在△AOC中, = 。 解:连接AO并延长与⊙O交与点D
∴ ∠ =∠ 。 ∵在△AOB中, = 。
又∵∠BOC=∠ +∠ . ∴ ∠ =∠ 。
∴∠A= ∠BOC. 又∵∠BOD=∠ +∠ .
∴∠BAD= ∠BOD.
同理:∠CAD= ∠COD.
又∵∠BAC=∠BAD+∠CAD, ∠BOC=∠BOD+∠COD
∴∠BAC= ∠BOC.
(3) 圆心在圆周角的外部(如图3)想一想如何解?
由此得出:圆周角定理:
一条弧所对的圆周角等于该弧所对的圆心角的一半。
圆周角定理的推论1:
在同圆或等圆中,同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧也相等。
思考:“同弧”能否改成“同弦”呢?同弦所对的圆周角一定相等吗?
学以致用1:试分别求出图中∠x的度数。
跟踪练习:
如下左图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线同侧,∠BAC=350
(1)∠BDC=_______°,理由是_______________________.
(2)∠BOC=_______°,理由是_______________________.
学以致用2: 在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,
则这条弧所对的圆心角和圆周角的度数分别为 。
学以致用3::.如上右图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB 与∠COA 相等吗?为什么?
典型例题:
例1.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,
若∠ABC= ∠CAD,求弦AC的长.
例2.如图,⊙O的半径为1,AB是⊙O 的一条弦,
且AB=,则弦AB所对圆周角的度数为( )
(A)30° (B)60°(C)30°或150° (D)60°或120°
例3.如下左图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。
跟踪练习:如上右图,点A、B、C在⊙O上,点D在⊙O内,点A与点D在点B、C所在直线的同侧,比较∠BAC与∠BDC的大小,并说明理由.
例4.如下左图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
跟踪练习:如下右图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.130°
1、如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8
个角中,有几对相等的角?请把它们分别表示出来:
___________________________________________________.
3、如图,AB是⊙O的直径,∠BOC=120°,CD⊥AB,则∠ABD=___________。
4、如图,△ABC的3个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与
∠BCE相等的角有______________________。
5.(中考题)如下左图,于,若,则
如图5,求∠1+∠2+∠3+∠4+∠5= .
7.如上右图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
8.如右图,A、B、C、P是圆上的点,∠APC=∠CPB=60°。
求证:△ABC是等边三角形
9.人们常用“一字之差,差之千里”来形容因一点小小的差别,会给问题本身带来很大的区别。在数学中,这样例子比比皆是,下面两句话,先请你找出其中微小的区别,再比较解决问题结果:
(1)在⊙O中,一条弧所对的圆心角是120°,该弧所对的圆周角是多少度?
(2)在⊙O中,一条弦所对的圆心角是120°,该弦所对的圆周角是多少度?
预 习 检 测
课 前 准 备
交 流 合 作
D
A
A
B
C
O
B
C
O
图2
图3
D
A
O
B
C
图1
B
A
O
.
70°
x
A
O
.
X
130°°
35°
32°
x
达 标 检 测
序 号: ( 5 )
年 级: 九年级 单元名称:第28章 圆
课 型: 新授课 上课时间:
学习内容:华东师大版课本 页
学习目标:
1.理解圆周角的概念,
2.掌握圆周角定理及其推论的内容及简单应用;
3.经历探索圆周角定理的过程,体会分类、转化等数学思想方法。
重 点:圆周角的概念和圆周角定理及推论。
难 点:圆周角定理的证明中由“一般到特殊”的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想方法和分类的数学 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网" \t "_blank )思想.
学法指导:合作探究
学 习 过 程
自主预习课本 页,完成下列各题:
圆周角的定义
顶点在 ,并且两边都和圆 的角叫做圆周角.
2.判断下列各图中的角是否是圆周角。
及
3.圆周角定理:
1、圆心角的定义: 。
2.圆心角、弧、弦、弦心距关系定理:
在定理中注意不能丢掉 这个前提。
3.什么叫弧?弧分哪几种?
探究:弧与圆心角的关系
问题导学:
1.在一个圆中,任作一个圆心角,它对应的弧有几条吗?
任作一条弧,它对应的圆心角有几个?
如图所示,圆心角对应的是弧AB。
这就说明:弧与圆心角的对应关系是唯一的。
2.当圆心角逐渐增大时,它对应的弧怎样变化?当圆心角减小时,它对应的弧又怎么变化?
这就说明:弧的大小会随着它对应的圆心角的大小而变化。
圆中最大的弧是什么?此时它对应的圆心角是什么?这个圆心角是多少度?
这就说明:整个圆周也是一段弧,它对应的圆心角是个周角,等于360度。
此时,我们就说整个圆周这段弧的度数就是它对应的圆心角的度数,等于360度。
半圆是弧吗?它对应的圆心角等于多少度?
这就说明:半圆这段弧的度数就是它对应的圆心角的度数,等于180度。
如果把圆周四等分,每段弧是多少度呢?六等分呢?10等分呢?n等分呢?
综上,我们得到这样的结论:
弧是有度数的,它的度数等于它所对应的圆心角的度数。
学以致用1:如图以ABCD的顶点A为圆心,AB为半径作圆,分别交BC、AD于E、F,若
∠D=50°,求弧BE的度数和弧BF的度数.
学以致用2.如图,弦AB把圆周分成1:2的两部分,已知⊙O半径为1,求弦长AB.
探究:什么叫圆周角?
1、圆周角定义: 。
圆周角有两个特征:① 。② 。
2、判别下列各图形中的角是不是圆周角,并说明理由。
3.找出右图中所有的圆周角。
三.探究:圆周角定理
在一个圆中,同一段弧对应几个圆周角?
作图看看。
这些圆周角的大小怎样?测量看看。
这段弧所对的圆心角有几个?
4.这些圆周角和这个圆心角的大小有什么关系?测量看看。
由上述操作我们可以猜想:
在同一圆中,同弧所对的圆周角相等,都等于该弧所对的圆心角的一半。
为了验证这个猜想,如图所示,可将圆对折,使折痕经过圆心O 和圆周角的顶点A,这时可能出现三种情况:
圆心在圆周角的边上(如图1),
圆心在圆周角的内部(如图2)
(3) 圆心在圆周角的外部(如图3)
(1)圆心在圆周角的边上 (如图1) (2) 圆心在圆周角的内部(如图2)
解:∵在△AOC中, = 。 解:连接AO并延长与⊙O交与点D
∴ ∠ =∠ 。 ∵在△AOB中, = 。
又∵∠BOC=∠ +∠ . ∴ ∠ =∠ 。
∴∠A= ∠BOC. 又∵∠BOD=∠ +∠ .
∴∠BAD= ∠BOD.
同理:∠CAD= ∠COD.
又∵∠BAC=∠BAD+∠CAD, ∠BOC=∠BOD+∠COD
∴∠BAC= ∠BOC.
(3) 圆心在圆周角的外部(如图3)想一想如何解?
由此得出:圆周角定理:
一条弧所对的圆周角等于该弧所对的圆心角的一半。
圆周角定理的推论1:
在同圆或等圆中,同弧或等弧所对的圆周角相等;
在同圆或等圆中,相等的圆周角所对的弧也相等。
思考:“同弧”能否改成“同弦”呢?同弦所对的圆周角一定相等吗?
学以致用1:试分别求出图中∠x的度数。
跟踪练习:
如下左图,点A、B、C、D在⊙O上,点A与点D在点B、C所在直线同侧,∠BAC=350
(1)∠BDC=_______°,理由是_______________________.
(2)∠BOC=_______°,理由是_______________________.
学以致用2: 在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x-30)°,
则这条弧所对的圆心角和圆周角的度数分别为 。
学以致用3::.如上右图,AB、AC、BC都是⊙O的弦,∠CAB=∠CBA,∠COB 与∠COA 相等吗?为什么?
典型例题:
例1.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,
若∠ABC= ∠CAD,求弦AC的长.
例2.如图,⊙O的半径为1,AB是⊙O 的一条弦,
且AB=,则弦AB所对圆周角的度数为( )
(A)30° (B)60°(C)30°或150° (D)60°或120°
例3.如下左图,点A、B、C在⊙O上,点D在圆外,CD、BD分别交⊙O于点E、F,比较∠BAC与∠BDC的大小,并说明理由。
跟踪练习:如上右图,点A、B、C在⊙O上,点D在⊙O内,点A与点D在点B、C所在直线的同侧,比较∠BAC与∠BDC的大小,并说明理由.
例4.如下左图,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
跟踪练习:如下右图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.130°
1、如图,△ABC的3个顶点都在⊙O上,∠ACB=40°,则∠AOB=_______,∠OAB=_____。
2.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,在这8
个角中,有几对相等的角?请把它们分别表示出来:
___________________________________________________.
3、如图,AB是⊙O的直径,∠BOC=120°,CD⊥AB,则∠ABD=___________。
4、如图,△ABC的3个顶点都在⊙O上,∠BAC的平分线交BC于点D,交⊙O于点E,则与
∠BCE相等的角有______________________。
5.(中考题)如下左图,于,若,则
如图5,求∠1+∠2+∠3+∠4+∠5= .
7.如上右图,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2
C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
8.如右图,A、B、C、P是圆上的点,∠APC=∠CPB=60°。
求证:△ABC是等边三角形
9.人们常用“一字之差,差之千里”来形容因一点小小的差别,会给问题本身带来很大的区别。在数学中,这样例子比比皆是,下面两句话,先请你找出其中微小的区别,再比较解决问题结果:
(1)在⊙O中,一条弧所对的圆心角是120°,该弧所对的圆周角是多少度?
(2)在⊙O中,一条弦所对的圆心角是120°,该弦所对的圆周角是多少度?
预 习 检 测
课 前 准 备
交 流 合 作
D
A
A
B
C
O
B
C
O
图2
图3
D
A
O
B
C
图1
B
A
O
.
70°
x
A
O
.
X
130°°
35°
32°
x
达 标 检 测
