5.2运动的合成与分解 教学课件(共21张PPT)-高一物理人教版(2019)必修第二册
文档属性
| 名称 | 5.2运动的合成与分解 教学课件(共21张PPT)-高一物理人教版(2019)必修第二册 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-30 16:24:59 | ||
图片预览







文档简介
(共21张PPT)
第五章 抛体运动
第2节 运动的合成与分解
问题与目标
1.结合实际生活,在具体的情境中,知道什么是合运动和分运动,知道其同时性和独立性。
2.知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则。
3.通过学习会用作图和计算的方法,求解位移和速度的合成与分解问题。
通过上节课的学习,我们大致对曲线运动有了一个了解,但是我们还不能像直线运动那样,能去用公式去准确的计算曲线运动的物理量。要研究曲线运动需要什么样的方法呢?这节课我们就来学习一下这个问题。
一、一个平面运动的实例
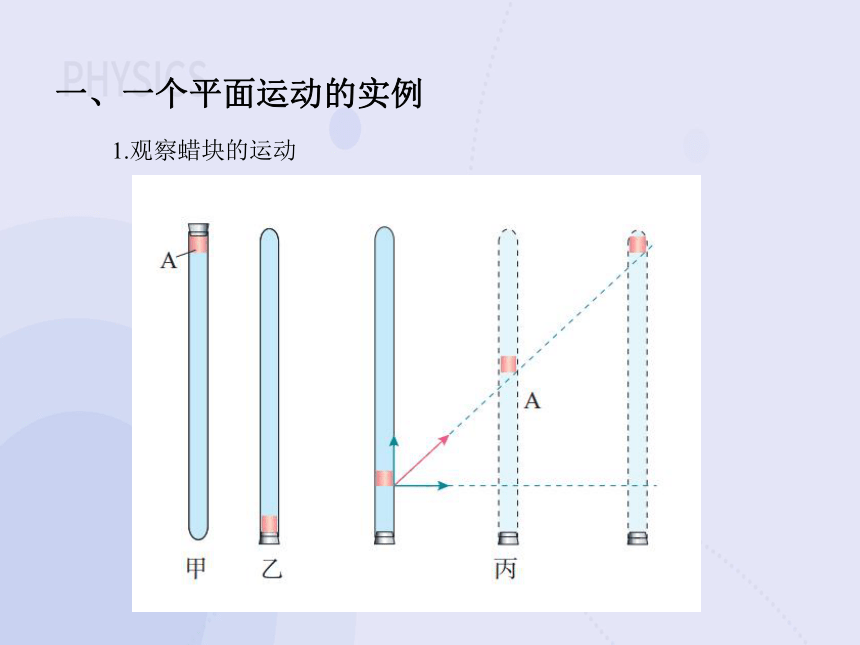
1.观察蜡块的运动
步骤①在一端封闭、长约1m的玻璃管内注满清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧(如图甲)。
步骤②把玻璃管倒置(如图乙),蜡块A沿玻璃管上升。如果在玻璃管旁边竖立一把刻度尺,可以看到,蜡块上升的速度大致不变,即蜡块做匀速直线运动。蜡块做匀速直线运动的原因是:蜡的密度略小于水的密度。在蜡块上升的初期,它做加速运动,随后由于受力平衡而做匀速运动。
步骤③在蜡块匀速上升的同时,将玻璃管紧贴着黑板沿水平方向向右匀速移动(如图丙),观察蜡块的运动情况。
这个实验中,蜡块既向上做匀速直线运动,又向右做匀速直线运动,以黑板为背景我们看到蜡块向右上方运动。那么,蜡块向右上方的运动是什么样的运动呢?
直线运动?
曲线运动?
我们可以用建立坐标系的方式来精确描述一下运动轨迹,这样就可以判断出到底是直线运动还是曲线运动。
2.建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向.上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
要确定蜡块运动的轨迹,首先要确定任意时刻蜡块的位置。我们如何写出蜡块的坐标随时间变化的关系式?
起点
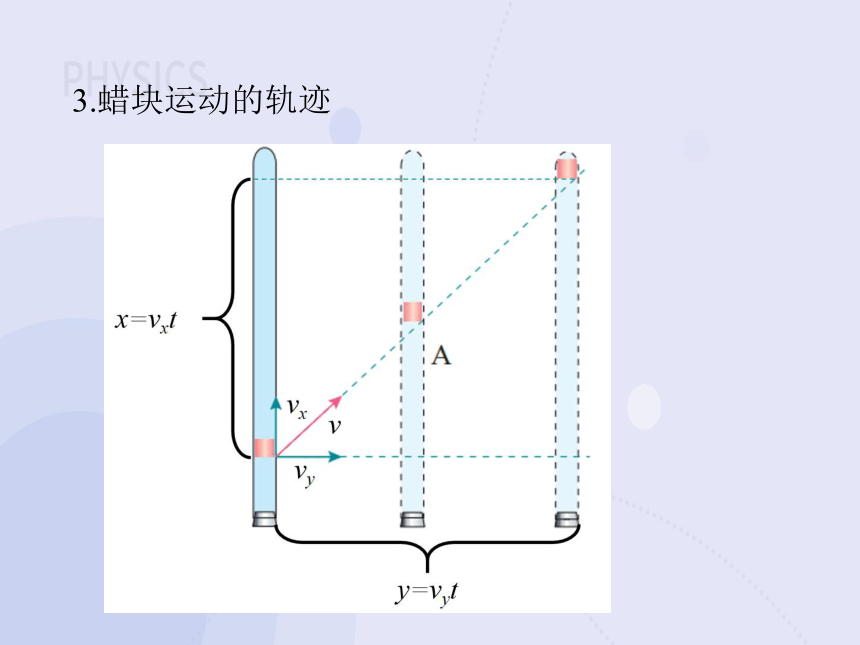
3.蜡块运动的轨迹
在数学上,关于x、y两个变量的关系式可以描述一条曲线(包括直线),而在上面x、y的表达式中,除了x、y之外还有一个变量t,我们可以从中消去t,这样就得到
4.蜡块运动的速度
速度v与vx、vy的关系已经在上图中形象地标出,因此可以根据勾股定理写出它们之间的关系:
二、运动的合成与分解
在这个实例中,我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于黑板向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成;由合运动求分运动的过程,叫作运动的分解。运动的合成与分解遵从矢量运算法则。
1.关于合运动、分运动的说法,正确的是( )
A.合运动的位移为分运动位移的矢量和
B.合运动的位移一定比其中的一个分位移大
C.合运动的速度一定比其中的一个分速度大
D.合运动的时间一定比分运动的时间长
1.答案:A
解析:位移是矢量,其运算遵循平行四边形定则,A正确;合运动的位移可大于分位移,也可小于分位移,还可等于分位移,B错误;同理可知C错误;合运动和分运动具有等时性,D错误。
2.答案:B
解析:热气球的实际运动为水平向右的匀速直线运动和竖直向上的匀加速直线运动的合运动,这类似于平抛运动,热气球的运动轨迹是抛物线,即B正确。
4.某质点在几个恒力作用下做匀速直线运动,现突然将与质点速度方向相反的一个力旋转90°,则关于质点运动状况的叙述正确的是( )
A.质点的速度一定越来越小
B.质点的速度可能先变大后变小
C.质点一定做匀变速曲线运动
D.因惯性质点继续保持匀速直线运动
第五章 抛体运动
第2节 运动的合成与分解
问题与目标
1.结合实际生活,在具体的情境中,知道什么是合运动和分运动,知道其同时性和独立性。
2.知道运动的合成与分解,理解运动的合成与分解遵循平行四边形定则。
3.通过学习会用作图和计算的方法,求解位移和速度的合成与分解问题。
通过上节课的学习,我们大致对曲线运动有了一个了解,但是我们还不能像直线运动那样,能去用公式去准确的计算曲线运动的物理量。要研究曲线运动需要什么样的方法呢?这节课我们就来学习一下这个问题。
一、一个平面运动的实例
1.观察蜡块的运动
步骤①在一端封闭、长约1m的玻璃管内注满清水,水中放一个红蜡做的小圆柱体A,将玻璃管的开口端用橡胶塞塞紧(如图甲)。
步骤②把玻璃管倒置(如图乙),蜡块A沿玻璃管上升。如果在玻璃管旁边竖立一把刻度尺,可以看到,蜡块上升的速度大致不变,即蜡块做匀速直线运动。蜡块做匀速直线运动的原因是:蜡的密度略小于水的密度。在蜡块上升的初期,它做加速运动,随后由于受力平衡而做匀速运动。
步骤③在蜡块匀速上升的同时,将玻璃管紧贴着黑板沿水平方向向右匀速移动(如图丙),观察蜡块的运动情况。
这个实验中,蜡块既向上做匀速直线运动,又向右做匀速直线运动,以黑板为背景我们看到蜡块向右上方运动。那么,蜡块向右上方的运动是什么样的运动呢?
直线运动?
曲线运动?
我们可以用建立坐标系的方式来精确描述一下运动轨迹,这样就可以判断出到底是直线运动还是曲线运动。
2.建立坐标系
以蜡块开始匀速运动的位置为原点O,以水平向右的方向和竖直向.上的方向分别为x轴和y轴的方向,建立平面直角坐标系。
要确定蜡块运动的轨迹,首先要确定任意时刻蜡块的位置。我们如何写出蜡块的坐标随时间变化的关系式?
起点
3.蜡块运动的轨迹
在数学上,关于x、y两个变量的关系式可以描述一条曲线(包括直线),而在上面x、y的表达式中,除了x、y之外还有一个变量t,我们可以从中消去t,这样就得到
4.蜡块运动的速度
速度v与vx、vy的关系已经在上图中形象地标出,因此可以根据勾股定理写出它们之间的关系:
二、运动的合成与分解
在这个实例中,我们看到蜡块向右上方的运动可以看成由沿玻璃管向上的运动和水平向右的运动共同构成。蜡块沿玻璃管向上的运动和它随着玻璃管向右的运动,都叫作分运动;而蜡块相对于黑板向右上方的运动叫作合运动。
由分运动求合运动的过程,叫作运动的合成;由合运动求分运动的过程,叫作运动的分解。运动的合成与分解遵从矢量运算法则。
1.关于合运动、分运动的说法,正确的是( )
A.合运动的位移为分运动位移的矢量和
B.合运动的位移一定比其中的一个分位移大
C.合运动的速度一定比其中的一个分速度大
D.合运动的时间一定比分运动的时间长
1.答案:A
解析:位移是矢量,其运算遵循平行四边形定则,A正确;合运动的位移可大于分位移,也可小于分位移,还可等于分位移,B错误;同理可知C错误;合运动和分运动具有等时性,D错误。
2.答案:B
解析:热气球的实际运动为水平向右的匀速直线运动和竖直向上的匀加速直线运动的合运动,这类似于平抛运动,热气球的运动轨迹是抛物线,即B正确。
4.某质点在几个恒力作用下做匀速直线运动,现突然将与质点速度方向相反的一个力旋转90°,则关于质点运动状况的叙述正确的是( )
A.质点的速度一定越来越小
B.质点的速度可能先变大后变小
C.质点一定做匀变速曲线运动
D.因惯性质点继续保持匀速直线运动
