2022-2023学年高一下学期物理人教版(2019)必修第二册6.1.2 圆周运动(多解问题、追及问题)课件(14张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期物理人教版(2019)必修第二册6.1.2 圆周运动(多解问题、追及问题)课件(14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-30 17:02:13 | ||
图片预览


文档简介
(共14张PPT)
§6.12 圆周运动
(多解问题、追及问题)
第六章 圆周运动
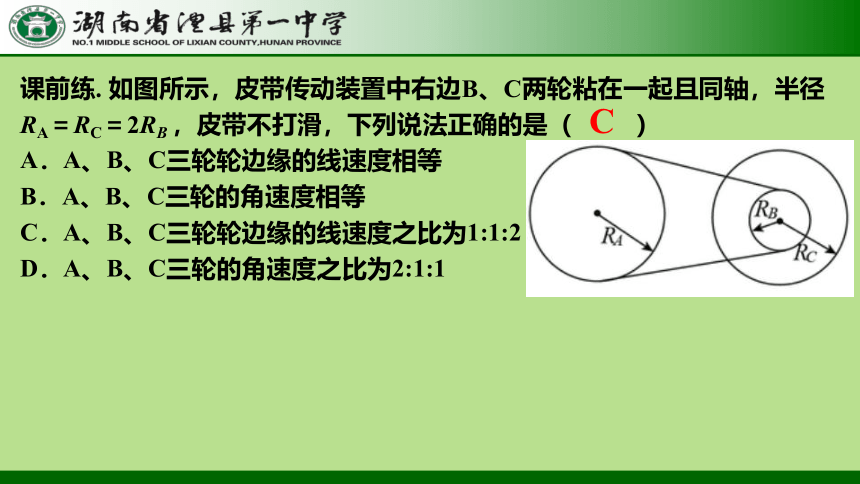
课前练. 如图所示,皮带传动装置中右边B、C两轮粘在一起且同轴,半径RA=RC=2RB ,皮带不打滑,下列说法正确的是( )
A.A、B、C三轮轮边缘的线速度相等
B.A、B、C三轮的角速度相等
C.A、B、C三轮轮边缘的线速度之比为1:1:2
D.A、B、C三轮的角速度之比为2:1:1
C
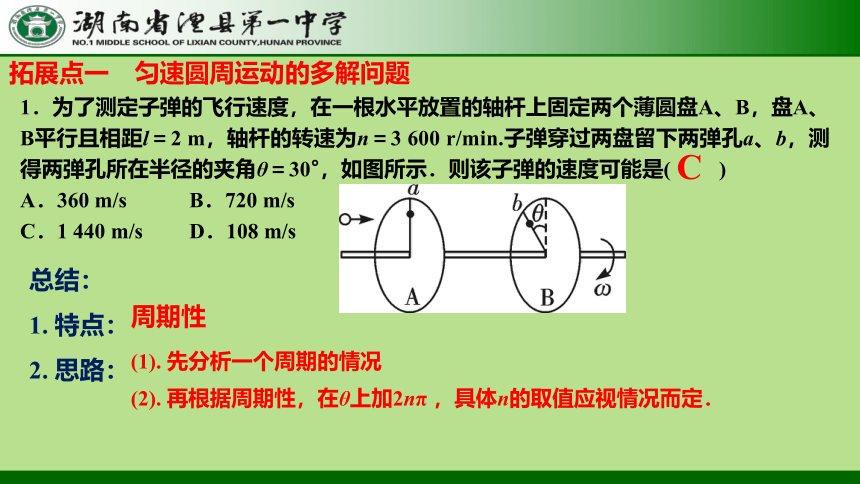
1.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距l=2 m,轴杆的转速为n=3 600 r/min.子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示.则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
拓展点一 匀速圆周运动的多解问题
总结:
1. 特点:
2. 思路:
周期性
(1). 先分析一个周期的情况
(2). 再根据周期性,在θ上加2nπ ,具体n的取值应视情况而定.
C
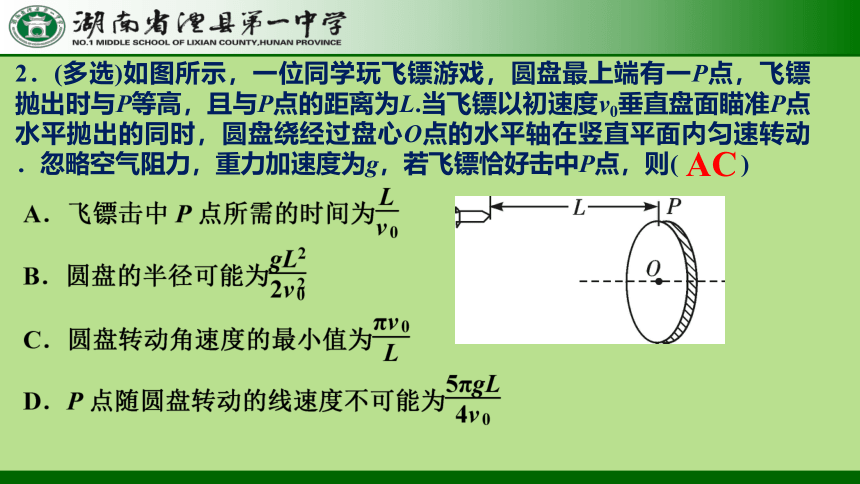
2.(多选)如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且与P点的距离为L.当飞镖以初速度v0垂直盘面瞄准P点水平抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
AC
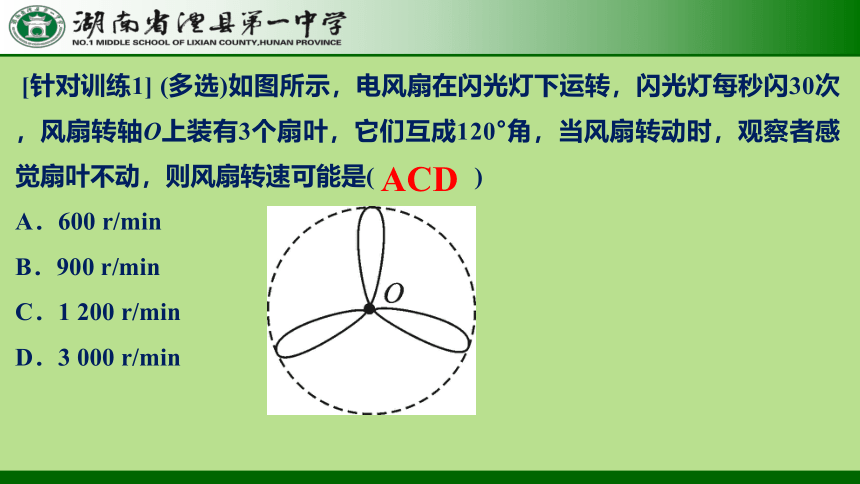
[针对训练1] (多选)如图所示,电风扇在闪光灯下运转,闪光灯每秒闪30次,风扇转轴O上装有3个扇叶,它们互成120°角,当风扇转动时,观察者感觉扇叶不动,则风扇转速可能是( )
A.600 r/min
B.900 r/min
C.1 200 r/min
D.3 000 r/min
ACD
拓展点二 匀速圆周运动与其他运动的综合问题
圆周运动经常与平抛运动和直线运动等不同的运动相结合,虽然运动具有独立性,并遵循各自的运动规律,但不同的运动规律在解决同一问题时,必然有一个物理量起“桥梁”作用,将两种不同的运动联系起来,这个“桥梁”常常是时间.分析求解具体问题时,也要特别注意由圆周运动而引起的多解的情况.
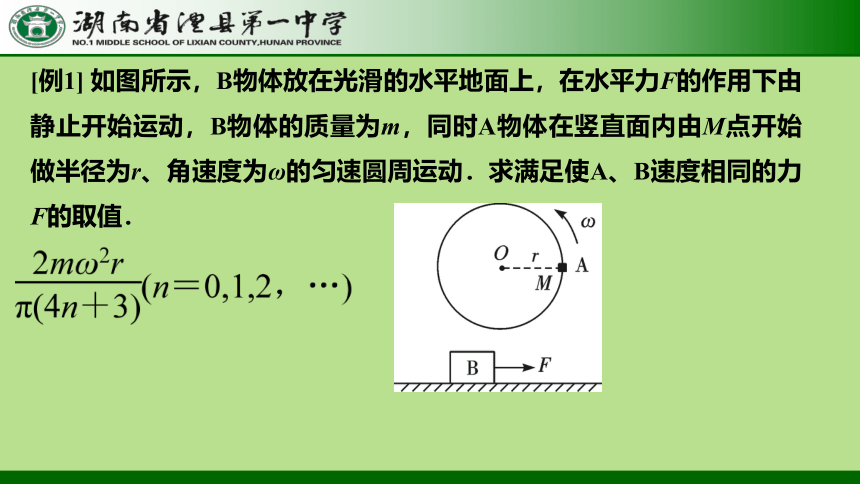
[例1] 如图所示,B物体放在光滑的水平地面上,在水平力F的作用下由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动.求满足使A、B速度相同的力F的取值.
[例2] 如图所示,半径为R的圆轮在竖直面内绕O轴匀速转动,O轴离地面高为2R,轮上a、b两点与O点的连线互相垂直,a、b两点均粘有一个小物体.当a点转至最低位置时,a、b两点处的小物体同时脱落,经过相同时间落到水平地面上.
(1)试判断圆轮的转动方向;
(2)求圆轮转动的角速度.(重力加速度为g)
[针对训练2] 如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其圆心O正上方h处沿OB方向水平抛出一个小球,要使球与盘只碰一次,且落点为B,求:
(1)小球的初速度;
(2)圆盘转动的角速度ω.
3.如图所示,光滑桌面上一个小球由于细线的牵引,绕桌面上的图钉做匀速圆周运动,已知角速度为6 rad/s,圆周半径为0.5 m,桌面离地高度为0.8 m.求:(g取10 m/s2)
(1)小球的线速度大小;
(2)某时刻细线突然断了,
小球离开桌面后做平抛运动所用的时间;
(3)小球落地前瞬间的速度大小.
(1)3 m/s (2)0.4 s (3)5 m/s
4.如图所示,M是水平放置的半径足够大的圆盘,可绕过其圆心的竖直轴OO′匀速转动,在圆心O正上方h处有一个正在不断滴水的容器,每当一滴水落在盘面时恰好下一滴水离开滴口.某次一滴水离开滴口时,容器恰好开始水平向右做速度为v的匀速直线运动,将此滴水记作第一滴水.不计空气阻力,重力加速度为g.求:
(1)相邻两滴水下落的时间间隔;
(2)要使每一滴水在盘面上的落点都在一条直线上,圆盘转动的角速度;
(3)第二滴水和第三滴水在盘面上落点之间的最大距离.
例. 设金星和地球绕太阳中心的运动是公转方向相同且轨道共面的匀速圆周运动,金星在地球轨道的内侧(称为地内行星)。在某些特殊时刻,地球、金星和太阳会出现在一条直线上,这时候从地球上观测,金星像镶嵌在太阳脸上的小黑痣缓慢走过太阳表面。天文学称这种现象为“金星凌日”。如图所示,2012年6月6日天空上演的“金星凌日”吸引了全世界数百万天文爱好者。假设所有行星都在绕太阳做匀速圆周运动,地球的公转周期为T1 , 金星的公转周期为T2(T1>T2),则“金星凌日”每隔多少年出现一次?
拓展点三 追及问题
变式. 若某时刻分针时针重合,则下次重合还要经过多少时间?
若某时刻分针时针重合,经多长时间分针时针处于同一直线?
转的快的多转一圈或半圈
n(h) (n = 1 , 2 , 3 )
(h) (k = 0 , 1 , 2 , 3
拓展点一 匀速圆周运动的多解问题
1. 特点:
2. 思路:
周期性
(1). 先分析一个周期的情况
(2). 再根据周期性,在θ上加2nπ ,具体n的取值应视情况而定.
拓展点二 匀速圆周运动与其他运动的综合问题
拓展点三 追及问题
课堂小结
时间起“桥梁”作用;周期性
转的快的多转一圈或半圈;周期性
§6.12 圆周运动
(多解问题、追及问题)
第六章 圆周运动
课前练. 如图所示,皮带传动装置中右边B、C两轮粘在一起且同轴,半径RA=RC=2RB ,皮带不打滑,下列说法正确的是( )
A.A、B、C三轮轮边缘的线速度相等
B.A、B、C三轮的角速度相等
C.A、B、C三轮轮边缘的线速度之比为1:1:2
D.A、B、C三轮的角速度之比为2:1:1
C
1.为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距l=2 m,轴杆的转速为n=3 600 r/min.子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示.则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
拓展点一 匀速圆周运动的多解问题
总结:
1. 特点:
2. 思路:
周期性
(1). 先分析一个周期的情况
(2). 再根据周期性,在θ上加2nπ ,具体n的取值应视情况而定.
C
2.(多选)如图所示,一位同学玩飞镖游戏,圆盘最上端有一P点,飞镖抛出时与P等高,且与P点的距离为L.当飞镖以初速度v0垂直盘面瞄准P点水平抛出的同时,圆盘绕经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
AC
[针对训练1] (多选)如图所示,电风扇在闪光灯下运转,闪光灯每秒闪30次,风扇转轴O上装有3个扇叶,它们互成120°角,当风扇转动时,观察者感觉扇叶不动,则风扇转速可能是( )
A.600 r/min
B.900 r/min
C.1 200 r/min
D.3 000 r/min
ACD
拓展点二 匀速圆周运动与其他运动的综合问题
圆周运动经常与平抛运动和直线运动等不同的运动相结合,虽然运动具有独立性,并遵循各自的运动规律,但不同的运动规律在解决同一问题时,必然有一个物理量起“桥梁”作用,将两种不同的运动联系起来,这个“桥梁”常常是时间.分析求解具体问题时,也要特别注意由圆周运动而引起的多解的情况.
[例1] 如图所示,B物体放在光滑的水平地面上,在水平力F的作用下由静止开始运动,B物体的质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动.求满足使A、B速度相同的力F的取值.
[例2] 如图所示,半径为R的圆轮在竖直面内绕O轴匀速转动,O轴离地面高为2R,轮上a、b两点与O点的连线互相垂直,a、b两点均粘有一个小物体.当a点转至最低位置时,a、b两点处的小物体同时脱落,经过相同时间落到水平地面上.
(1)试判断圆轮的转动方向;
(2)求圆轮转动的角速度.(重力加速度为g)
[针对训练2] 如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其圆心O正上方h处沿OB方向水平抛出一个小球,要使球与盘只碰一次,且落点为B,求:
(1)小球的初速度;
(2)圆盘转动的角速度ω.
3.如图所示,光滑桌面上一个小球由于细线的牵引,绕桌面上的图钉做匀速圆周运动,已知角速度为6 rad/s,圆周半径为0.5 m,桌面离地高度为0.8 m.求:(g取10 m/s2)
(1)小球的线速度大小;
(2)某时刻细线突然断了,
小球离开桌面后做平抛运动所用的时间;
(3)小球落地前瞬间的速度大小.
(1)3 m/s (2)0.4 s (3)5 m/s
4.如图所示,M是水平放置的半径足够大的圆盘,可绕过其圆心的竖直轴OO′匀速转动,在圆心O正上方h处有一个正在不断滴水的容器,每当一滴水落在盘面时恰好下一滴水离开滴口.某次一滴水离开滴口时,容器恰好开始水平向右做速度为v的匀速直线运动,将此滴水记作第一滴水.不计空气阻力,重力加速度为g.求:
(1)相邻两滴水下落的时间间隔;
(2)要使每一滴水在盘面上的落点都在一条直线上,圆盘转动的角速度;
(3)第二滴水和第三滴水在盘面上落点之间的最大距离.
例. 设金星和地球绕太阳中心的运动是公转方向相同且轨道共面的匀速圆周运动,金星在地球轨道的内侧(称为地内行星)。在某些特殊时刻,地球、金星和太阳会出现在一条直线上,这时候从地球上观测,金星像镶嵌在太阳脸上的小黑痣缓慢走过太阳表面。天文学称这种现象为“金星凌日”。如图所示,2012年6月6日天空上演的“金星凌日”吸引了全世界数百万天文爱好者。假设所有行星都在绕太阳做匀速圆周运动,地球的公转周期为T1 , 金星的公转周期为T2(T1>T2),则“金星凌日”每隔多少年出现一次?
拓展点三 追及问题
变式. 若某时刻分针时针重合,则下次重合还要经过多少时间?
若某时刻分针时针重合,经多长时间分针时针处于同一直线?
转的快的多转一圈或半圈
n(h) (n = 1 , 2 , 3 )
(h) (k = 0 , 1 , 2 , 3
拓展点一 匀速圆周运动的多解问题
1. 特点:
2. 思路:
周期性
(1). 先分析一个周期的情况
(2). 再根据周期性,在θ上加2nπ ,具体n的取值应视情况而定.
拓展点二 匀速圆周运动与其他运动的综合问题
拓展点三 追及问题
课堂小结
时间起“桥梁”作用;周期性
转的快的多转一圈或半圈;周期性
