圆和圆的位置关系
图片预览
文档简介
课 题:《圆和圆的位置关系》
序 号: ( 14 )
年 级: 九年级 单元名称:第28章 圆
课 型: 新授课 上课时间:
学习内容:华东师大版课本 页
学习目标:1.圆与圆之间的几种位置关系.
2.两圆圆心距d、半径R和r的数量关系的联系.
重 点:1.探索圆与圆之间的几种位置关系
2.两圆圆心距d、半径R和r的数量关系的联系
难 点:两圆圆心距d、半径R和r的数量关系的联系
学法指导:合作探究
学 习 过 程
自主预习课本 页,完成下列各题:
1.圆和圆的位置关系有______________________________________________________.
2.如果两圆的半径分别为R、r,圆心距为d,则
两圆外离 ________________ 两圆外切 ________________
两圆相交 ________________ 两圆内切 ________________
两圆内含 ________________
3.如果两圆的半径为5、9,圆心距为3,那么两圆的位置关系是 ( )
A外离 B相切 C相交 D 内含
4.⊙ 和⊙相内切,若=3,⊙的半径为7,则⊙的半径为 ( )
A 4 B 6 C 0 D以上都不对
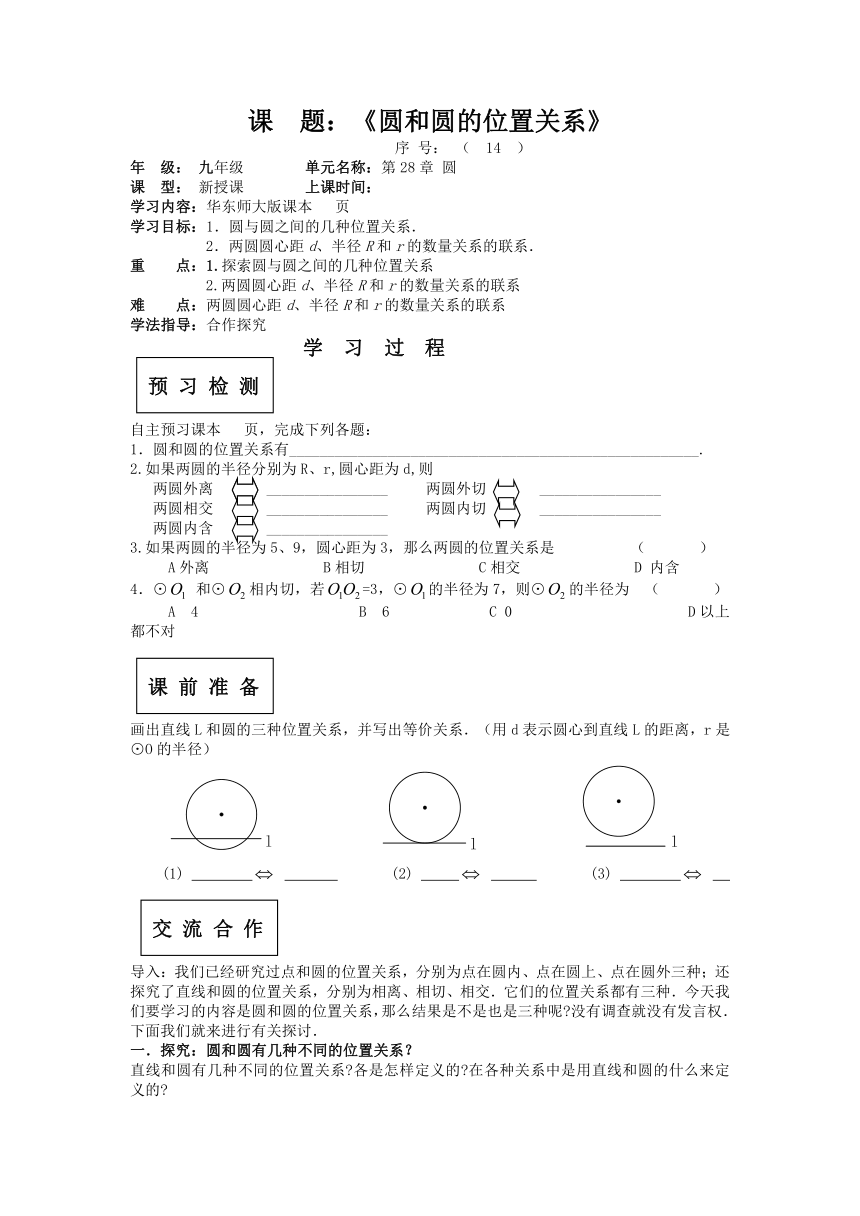
画出直线L和圆的三种位置关系,并写出等价关系.(用d表示圆心到直线L的距离,r是⊙O的半径)
(1) (2) (3)
导入:我们已经研究过点和圆的位置关系,分别为点在圆内、点在圆上、点在圆外三种;还探究了直线和圆的位置关系,分别为相离、相切、相交.它们的位置关系都有三种.今天我们要学习的内容是圆和圆的位置关系,那么结果是不是也是三种呢 没有调查就没有发言权.
下面我们就来进行有关探讨.
探究:圆和圆有几种不同的位置关系?
直线和圆有几种不同的位置关系 各是怎样定义的 在各种关系中是用直线和圆的什么来定义的
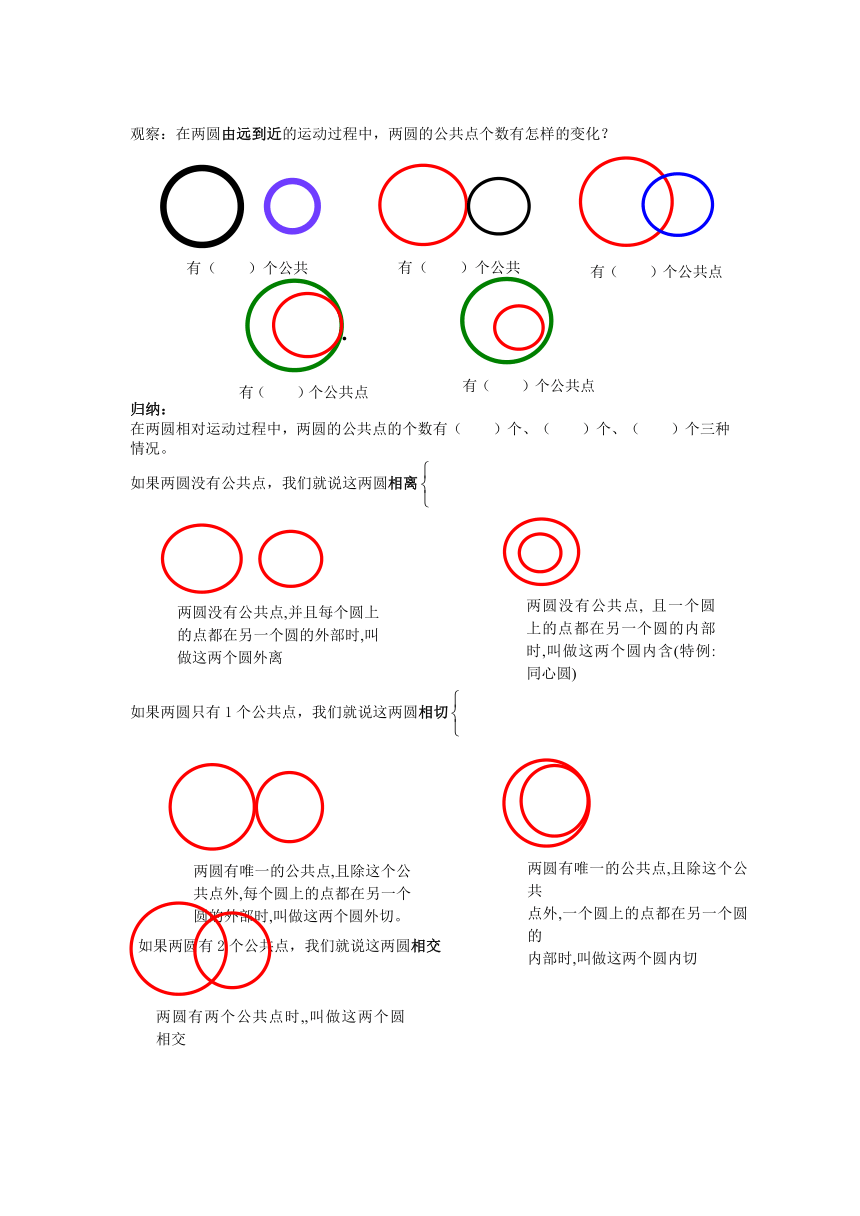
观察:在两圆由远到近的运动过程中,两圆的公共点个数有怎样的变化?
归纳:
在两圆相对运动过程中,两圆的公共点的个数有( )个、( )个、( )个三种情况。
如果两圆没有公共点,我们就说这两圆相离
如果两圆只有1个公共点,我们就说这两圆相切
如果两圆有2个公共点,我们就说这两圆相交
归纳:圆和圆的位置关系共有几种?
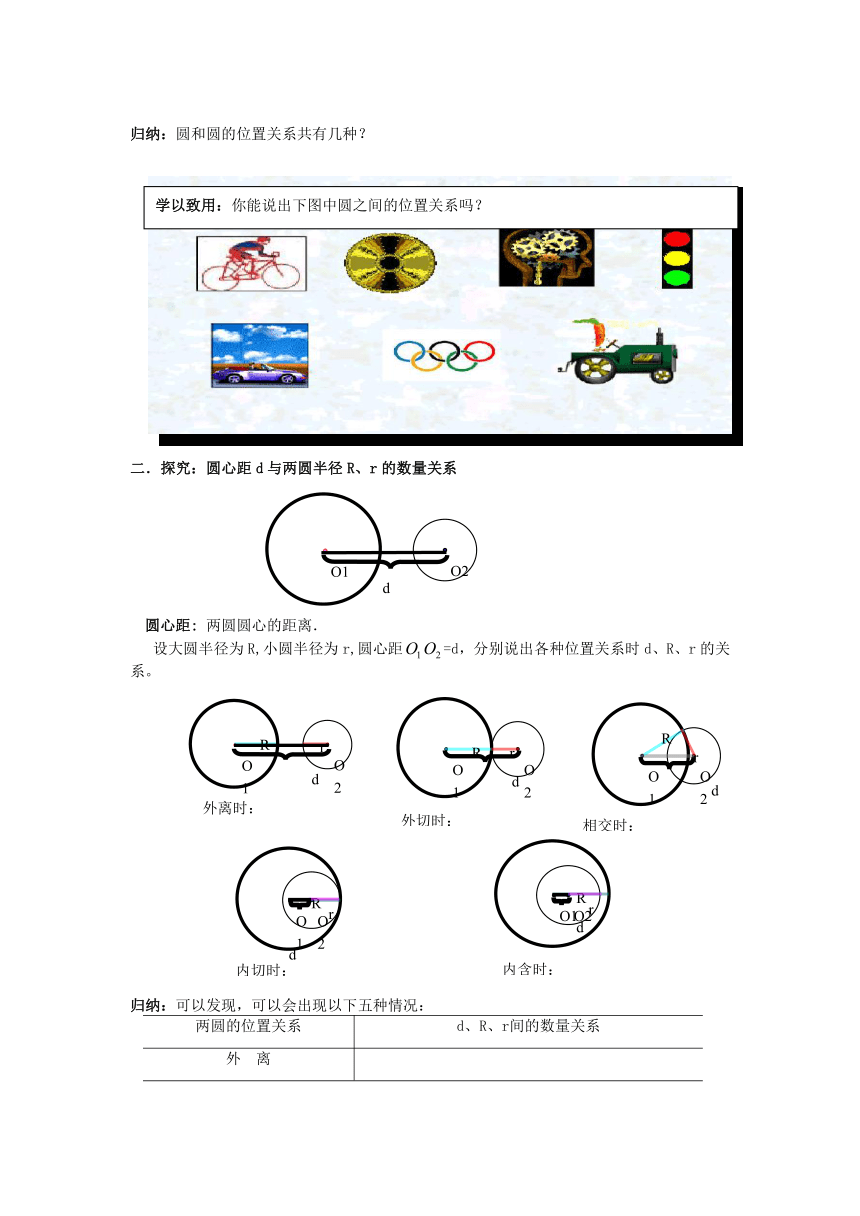
二.探究:圆心距d与两圆半径R、r的数量关系
圆心距: 两圆圆心的距离.
设大圆半径为R,小圆半径为r,圆心距=d,分别说出各种位置关系时d、R、r的关系。
归纳:可以发现,可以会出现以下五种情况:
两圆的位置关系 d、R、r间的数量关系
外 离
外 切
相 交
内 切
内 含
学以致用1:
(1)已知两圆的半径分别为2、5,且圆心距等于3,则两圆位置关系是 ( )
(A)外离 (B)外切 (C)相交 (D) 内切
(2)已知两圆的半径分别是2和4,圆心距是3,那么这两圆的位置是( )
(A)内含 (B)内切 (C)相交 (D) 外切
(3)两圆直径分别为6、8,圆心距为10,那么这两圆的位置是( )
(A)内含 (B)内切 (C)相交 (D) 外切
(4)已知⊙与⊙的半径分别为3 cm和4 cm,若=7 cm,则⊙与⊙的位置关系是( )
(A) 相交 (B) 相离 (C) 内切 (D) 外切
(5)已知两圆的半径分别为3、7,且圆心距等于2,则两圆位置关系是 ( )
(A)外离 (B)外切 (C)相交 (D) 内切
学以致用2:判断正误:
(1)、若两圆只有一个交点,则这两圆外切. ( )
(2)、如果两圆没有交点,则这两圆的位置关系是外离. ( )
(3)、当O1O2=0时,两圆位置关系是同心圆.( )
(4)、若O1O2=1.5,r=1,R=3,则O1O2(5)、若O1O2=3,且r =7,R=3,则O1O2学以致用3:两圆相内切,若圆心距为3,且一圆的半径为7,则另一圆的半径为 ( )
A 4 B 6 C 10 D 4或10
学以致用4:两圆半径为5和r,圆心距为8,当两圆相交时,r取值范围是
学以致用5:已知⊙A、⊙B 相切,圆心距为10cm,其中⊙A的半径为4cm,求⊙B 的半径.
J
跟踪练习:如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
(1) (2)
学以致用6:已知图中各圆两两相切,⊙O的半径为2R,⊙O1、⊙O2的半径为R,求⊙O3的半径.
学以致用7:如图,ΔABC的∠C=Rt∠,BC=4,AC=3,两个外切的等圆⊙O1,⊙O2各与AB,AC,BC相切于F,H,E,G,求两圆的半径。
学以致用8:如图,⊙O和⊙O1内切于E,大圆弦AD经过⊙O1且交⊙O1于B,C,AB:BC:CD=2:4:3,求⊙O1与⊙O半径之比。
1.两圆的圆心距d=4,两圆的半径分别是方程x2-5x+6=0的两个根,则两圆的位置关系是( )
A、外离 B、外切 C、相交 D、内切
2.已知⊙O1半径为3cm,⊙O2半径为4cm,并且⊙O1与⊙O2相切,则这两个圆的圆心距为( )
(A)1cm (B)7cm (C) 10cm (D) 1cm或7cm
3.两圆外切时圆心距为10cm,且这两圆半径之比为2:3,如果内含,那么这两圆的圆心距为( )
(A)小于10cm, (B)小于2cm (C)小于5cm (D)小于3cm
4.⊙O1和⊙O2的半径分别为3 cm和4cm,若两圆外切,则d=_____;若两圆内切d=__ __.
5.两圆的半径分别为10 cm和R、圆心距为13 cm,若这两个圆相切,则R的值是____.
6.半径为5 cm的⊙O外一点P,则以点P为圆心且与⊙O相切的⊙P能画_______个.
7.两圆半径之比为3:5,当两圆内切时,圆心距为4 cm,则两圆外切时圆心距的长为_____.
8.两圆内切时圆心距是2,这两圆外切时圆心距是5,两圆的半径分别是______、_______
9.两圆内切,圆心距为3,一个圆的半径为5,另一个圆的半径为 .
10.两个圆的半径的比为2 : 3 ,内切时圆心距等于 8cm,那么这两圆相交时,圆心距d的取值范围是
11.两圆内切,其圆心距为3 cm,一个圆半径为5 cm,则另一个圆的半径为
12.两圆相交,半径分别为3 cm和4 cm,圆心距为5 cm,则两圆的位置关系为
13.如图,⊙O1和⊙O2相切于点P,AB切两圆于A,B,ΔPAB的周长为40,面积为60,求P点到AB的距离。
14.如图,已知⊙O1和⊙O2相交于A,B,过A作直线分别交⊙O1,⊙O2于C,D,过B作直线分别交⊙O1,⊙O2于E,F,求证:CE∥DF
预 习 检 测
课 前 准 备
交 流 合 作
有( )个公共点
有( )个公共点
有( )个公共点
有( )个公共点
有( )个公共点
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆没有公共点, 且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(特例:同心圆)
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切。
两圆有唯一的公共点,且除这个公共
点外,一个圆上的点都在另一个圆的
内部时,叫做这两个圆内切
两圆有两个公共点时,,叫做这两个圆相交
学以致用:你能说出下图中圆之间的位置关系吗?
O1
O2
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
外: 外离时:
外切时:
相交时:
内切时:
内含时:
达 标 检 测
序 号: ( 14 )
年 级: 九年级 单元名称:第28章 圆
课 型: 新授课 上课时间:
学习内容:华东师大版课本 页
学习目标:1.圆与圆之间的几种位置关系.
2.两圆圆心距d、半径R和r的数量关系的联系.
重 点:1.探索圆与圆之间的几种位置关系
2.两圆圆心距d、半径R和r的数量关系的联系
难 点:两圆圆心距d、半径R和r的数量关系的联系
学法指导:合作探究
学 习 过 程
自主预习课本 页,完成下列各题:
1.圆和圆的位置关系有______________________________________________________.
2.如果两圆的半径分别为R、r,圆心距为d,则
两圆外离 ________________ 两圆外切 ________________
两圆相交 ________________ 两圆内切 ________________
两圆内含 ________________
3.如果两圆的半径为5、9,圆心距为3,那么两圆的位置关系是 ( )
A外离 B相切 C相交 D 内含
4.⊙ 和⊙相内切,若=3,⊙的半径为7,则⊙的半径为 ( )
A 4 B 6 C 0 D以上都不对
画出直线L和圆的三种位置关系,并写出等价关系.(用d表示圆心到直线L的距离,r是⊙O的半径)
(1) (2) (3)
导入:我们已经研究过点和圆的位置关系,分别为点在圆内、点在圆上、点在圆外三种;还探究了直线和圆的位置关系,分别为相离、相切、相交.它们的位置关系都有三种.今天我们要学习的内容是圆和圆的位置关系,那么结果是不是也是三种呢 没有调查就没有发言权.
下面我们就来进行有关探讨.
探究:圆和圆有几种不同的位置关系?
直线和圆有几种不同的位置关系 各是怎样定义的 在各种关系中是用直线和圆的什么来定义的
观察:在两圆由远到近的运动过程中,两圆的公共点个数有怎样的变化?
归纳:
在两圆相对运动过程中,两圆的公共点的个数有( )个、( )个、( )个三种情况。
如果两圆没有公共点,我们就说这两圆相离
如果两圆只有1个公共点,我们就说这两圆相切
如果两圆有2个公共点,我们就说这两圆相交
归纳:圆和圆的位置关系共有几种?
二.探究:圆心距d与两圆半径R、r的数量关系
圆心距: 两圆圆心的距离.
设大圆半径为R,小圆半径为r,圆心距=d,分别说出各种位置关系时d、R、r的关系。
归纳:可以发现,可以会出现以下五种情况:
两圆的位置关系 d、R、r间的数量关系
外 离
外 切
相 交
内 切
内 含
学以致用1:
(1)已知两圆的半径分别为2、5,且圆心距等于3,则两圆位置关系是 ( )
(A)外离 (B)外切 (C)相交 (D) 内切
(2)已知两圆的半径分别是2和4,圆心距是3,那么这两圆的位置是( )
(A)内含 (B)内切 (C)相交 (D) 外切
(3)两圆直径分别为6、8,圆心距为10,那么这两圆的位置是( )
(A)内含 (B)内切 (C)相交 (D) 外切
(4)已知⊙与⊙的半径分别为3 cm和4 cm,若=7 cm,则⊙与⊙的位置关系是( )
(A) 相交 (B) 相离 (C) 内切 (D) 外切
(5)已知两圆的半径分别为3、7,且圆心距等于2,则两圆位置关系是 ( )
(A)外离 (B)外切 (C)相交 (D) 内切
学以致用2:判断正误:
(1)、若两圆只有一个交点,则这两圆外切. ( )
(2)、如果两圆没有交点,则这两圆的位置关系是外离. ( )
(3)、当O1O2=0时,两圆位置关系是同心圆.( )
(4)、若O1O2=1.5,r=1,R=3,则O1O2
A 4 B 6 C 10 D 4或10
学以致用4:两圆半径为5和r,圆心距为8,当两圆相交时,r取值范围是
学以致用5:已知⊙A、⊙B 相切,圆心距为10cm,其中⊙A的半径为4cm,求⊙B 的半径.
J
跟踪练习:如图所示,⊙O的半径为7cm,点A为⊙O外一点,OA=15cm,
求:(1)作⊙A与⊙O外切,并求⊙A的半径是多少?
(2)作⊙A与⊙O相内切,并求出此时⊙A的半径.
(1) (2)
学以致用6:已知图中各圆两两相切,⊙O的半径为2R,⊙O1、⊙O2的半径为R,求⊙O3的半径.
学以致用7:如图,ΔABC的∠C=Rt∠,BC=4,AC=3,两个外切的等圆⊙O1,⊙O2各与AB,AC,BC相切于F,H,E,G,求两圆的半径。
学以致用8:如图,⊙O和⊙O1内切于E,大圆弦AD经过⊙O1且交⊙O1于B,C,AB:BC:CD=2:4:3,求⊙O1与⊙O半径之比。
1.两圆的圆心距d=4,两圆的半径分别是方程x2-5x+6=0的两个根,则两圆的位置关系是( )
A、外离 B、外切 C、相交 D、内切
2.已知⊙O1半径为3cm,⊙O2半径为4cm,并且⊙O1与⊙O2相切,则这两个圆的圆心距为( )
(A)1cm (B)7cm (C) 10cm (D) 1cm或7cm
3.两圆外切时圆心距为10cm,且这两圆半径之比为2:3,如果内含,那么这两圆的圆心距为( )
(A)小于10cm, (B)小于2cm (C)小于5cm (D)小于3cm
4.⊙O1和⊙O2的半径分别为3 cm和4cm,若两圆外切,则d=_____;若两圆内切d=__ __.
5.两圆的半径分别为10 cm和R、圆心距为13 cm,若这两个圆相切,则R的值是____.
6.半径为5 cm的⊙O外一点P,则以点P为圆心且与⊙O相切的⊙P能画_______个.
7.两圆半径之比为3:5,当两圆内切时,圆心距为4 cm,则两圆外切时圆心距的长为_____.
8.两圆内切时圆心距是2,这两圆外切时圆心距是5,两圆的半径分别是______、_______
9.两圆内切,圆心距为3,一个圆的半径为5,另一个圆的半径为 .
10.两个圆的半径的比为2 : 3 ,内切时圆心距等于 8cm,那么这两圆相交时,圆心距d的取值范围是
11.两圆内切,其圆心距为3 cm,一个圆半径为5 cm,则另一个圆的半径为
12.两圆相交,半径分别为3 cm和4 cm,圆心距为5 cm,则两圆的位置关系为
13.如图,⊙O1和⊙O2相切于点P,AB切两圆于A,B,ΔPAB的周长为40,面积为60,求P点到AB的距离。
14.如图,已知⊙O1和⊙O2相交于A,B,过A作直线分别交⊙O1,⊙O2于C,D,过B作直线分别交⊙O1,⊙O2于E,F,求证:CE∥DF
预 习 检 测
课 前 准 备
交 流 合 作
有( )个公共点
有( )个公共点
有( )个公共点
有( )个公共点
有( )个公共点
两圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离
两圆没有公共点, 且一个圆上的点都在另一个圆的内部时,叫做这两个圆内含(特例:同心圆)
两圆有唯一的公共点,且除这个公共点外,每个圆上的点都在另一个圆的外部时,叫做这两个圆外切。
两圆有唯一的公共点,且除这个公共
点外,一个圆上的点都在另一个圆的
内部时,叫做这两个圆内切
两圆有两个公共点时,,叫做这两个圆相交
学以致用:你能说出下图中圆之间的位置关系吗?
O1
O2
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
O1
O2
R
r
d
外: 外离时:
外切时:
相交时:
内切时:
内含时:
达 标 检 测
