导数的背景(文科)[上学期]
图片预览







文档简介
课件20张PPT。第二章 导数第二章 导数1、导数的背景2、导数的概念3、多项式函数的导数4、利用导数研究函数的单调性与极值5、利用导数求函数的最大值与最小值6、微积分建立的时代背景和历史意义
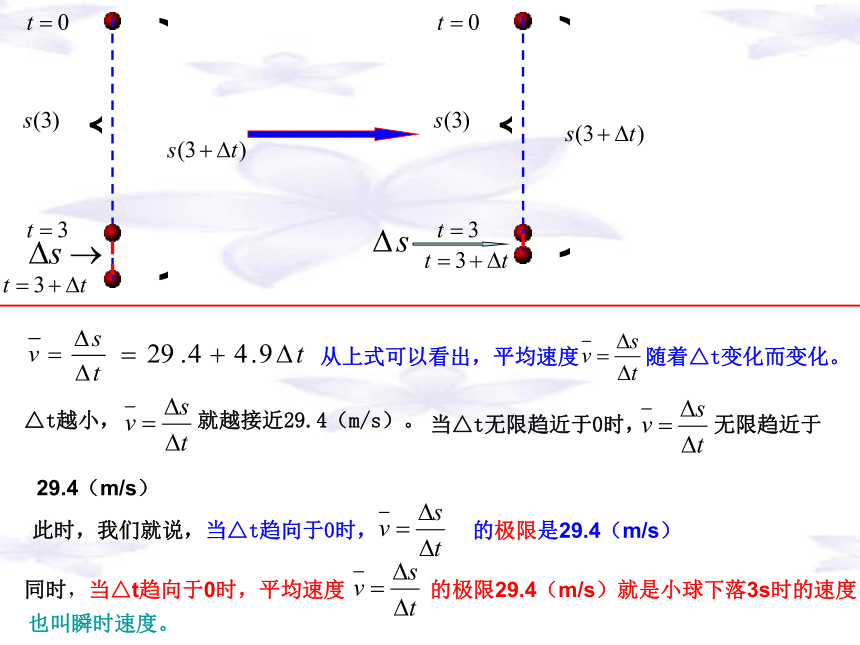
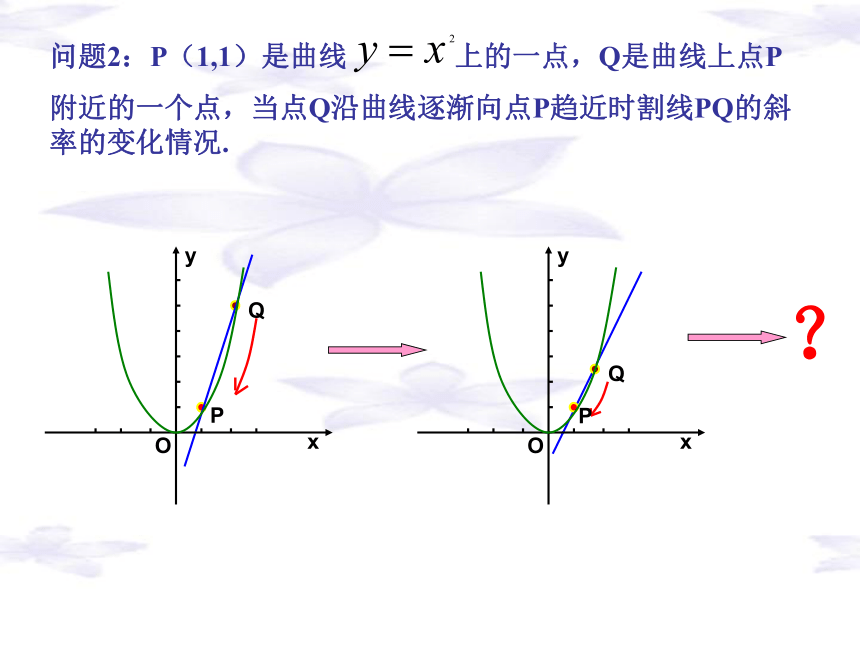
(同学自学)主要内容2.1 导数的背景一、导入新课问题1:一个小球自由下落,它在下落3秒时的速度是多少? 1、瞬时速度由物理实验得自由落体运动公式 (g取9.8m/s2)也可以计算某一段位移内的平均速度。可以计算匀速直线运动的速度;当时间增量△t很小时,从3s到(3+△t)s这段时间内,小球下落的的速度变化也不大。因此,可以用这段时间内的平均速度近似地看成是小球在下落3s时的速度。当△t越小,这种近似越精确。记从3s到(3+△t)s这段时间位移增量为△s,则 29.4(m/s)同时,当△t趋向于0时,平均速度的极限29.4(m/s)就是小球下落3s时的速度也叫瞬时速度。(1)一个小球自由下落,它在下落5秒时的速度是多少? 变式:(2)一个小球自由下落,它在下落 t 秒时的速度是多少? 答案:(1)49(m/s)(2)一、物理意义——瞬时速度当 越来越小的时候, 越来越接近某时刻的瞬时速度练习: PQ?(1+△x,(1+△x)2)求割线PQ的斜率:已知点P的坐标为(1,1),设点Q的横坐标为1+△x,则点Q的纵坐标是(1+△x)2利用两点的斜率公式:则点Q对点P的横坐标增量为△x,纵坐标增量△x△y由此可知,当点Q沿曲线逐渐向P接近时,△x越来越小,kPQ越来越接近2。当点Q沿曲线无限接近于点P时,△x无限趋近于0,kPQ无限趋近于2。此时,割线PQ就变成了曲线在点P的切线,且切线的斜率为2。曲线在点P的切线(1+△x,(1+△x)2)△x△y曲线在点P的切由点斜式公式知:即2、切线的斜率则点Q对点P的横坐标增量为△x,纵坐标增量割线PQ的斜率当点Q沿曲线逐渐向P接近时,割线PQ绕着点P在转动。当点Q沿曲线无限接近于点P时,△x无限趋近于0,割线无限趋近于一个极限位置PT。T那么直线PT叫做曲线在点P处的切线。3. 边际成本问题3:设成本为C,产量为q,成本与产量的函数关系式为
,
(1)当q=50时,增加单位产量,即产量变为51时,需付出的成本为多少?
(2)我们来研究当q=50时,产量变化对成本的影响。(2)在本问题中,成本的增量为: 分析:(1)增加单位产量需付出的成本为当 无限趋近于0时, 无限趋近于300,我们就说
当 趋向于0时, 的极限是300.
我们 把的极限300叫做当q=50时
的边际成本.
一般地,设C是成本,q是产量,成本与产量的函数关系式为C
=C(q),当产量为 时,产量变化对成本的影响可用增量
比
刻划. 如果 无限趋近于0时, 无限趋近于常数A,
经济学上称A为边际成本. 它表明当产量为 时,增加单位产量需付出成本A(这是实际付出成本的一个近似值).
三、实际应用——边际成本我们研究函数增量与自变量的关系:二、小结
1、 瞬时速度是平均速度 当 趋近于0时的极限;
2、切线是割线的极限位置,切线的斜率是割线斜率
当 趋近于0时的极限;
3、边际成本是平均成本 当 趋近于0时的极限.
练习: 1. 判断曲线 在点P(1,2)处是否有切线,如果
有,求出切线的方程.
2. 已知成本C与产量q的函数关系式为
,求当产量q=80时的边际成本.
布置作业布置作业
(同学自学)主要内容2.1 导数的背景一、导入新课问题1:一个小球自由下落,它在下落3秒时的速度是多少? 1、瞬时速度由物理实验得自由落体运动公式 (g取9.8m/s2)也可以计算某一段位移内的平均速度。可以计算匀速直线运动的速度;当时间增量△t很小时,从3s到(3+△t)s这段时间内,小球下落的的速度变化也不大。因此,可以用这段时间内的平均速度近似地看成是小球在下落3s时的速度。当△t越小,这种近似越精确。记从3s到(3+△t)s这段时间位移增量为△s,则 29.4(m/s)同时,当△t趋向于0时,平均速度的极限29.4(m/s)就是小球下落3s时的速度也叫瞬时速度。(1)一个小球自由下落,它在下落5秒时的速度是多少? 变式:(2)一个小球自由下落,它在下落 t 秒时的速度是多少? 答案:(1)49(m/s)(2)一、物理意义——瞬时速度当 越来越小的时候, 越来越接近某时刻的瞬时速度练习: PQ?(1+△x,(1+△x)2)求割线PQ的斜率:已知点P的坐标为(1,1),设点Q的横坐标为1+△x,则点Q的纵坐标是(1+△x)2利用两点的斜率公式:则点Q对点P的横坐标增量为△x,纵坐标增量△x△y由此可知,当点Q沿曲线逐渐向P接近时,△x越来越小,kPQ越来越接近2。当点Q沿曲线无限接近于点P时,△x无限趋近于0,kPQ无限趋近于2。此时,割线PQ就变成了曲线在点P的切线,且切线的斜率为2。曲线在点P的切线(1+△x,(1+△x)2)△x△y曲线在点P的切由点斜式公式知:即2、切线的斜率则点Q对点P的横坐标增量为△x,纵坐标增量割线PQ的斜率当点Q沿曲线逐渐向P接近时,割线PQ绕着点P在转动。当点Q沿曲线无限接近于点P时,△x无限趋近于0,割线无限趋近于一个极限位置PT。T那么直线PT叫做曲线在点P处的切线。3. 边际成本问题3:设成本为C,产量为q,成本与产量的函数关系式为
,
(1)当q=50时,增加单位产量,即产量变为51时,需付出的成本为多少?
(2)我们来研究当q=50时,产量变化对成本的影响。(2)在本问题中,成本的增量为: 分析:(1)增加单位产量需付出的成本为当 无限趋近于0时, 无限趋近于300,我们就说
当 趋向于0时, 的极限是300.
我们 把的极限300叫做当q=50时
的边际成本.
一般地,设C是成本,q是产量,成本与产量的函数关系式为C
=C(q),当产量为 时,产量变化对成本的影响可用增量
比
刻划. 如果 无限趋近于0时, 无限趋近于常数A,
经济学上称A为边际成本. 它表明当产量为 时,增加单位产量需付出成本A(这是实际付出成本的一个近似值).
三、实际应用——边际成本我们研究函数增量与自变量的关系:二、小结
1、 瞬时速度是平均速度 当 趋近于0时的极限;
2、切线是割线的极限位置,切线的斜率是割线斜率
当 趋近于0时的极限;
3、边际成本是平均成本 当 趋近于0时的极限.
练习: 1. 判断曲线 在点P(1,2)处是否有切线,如果
有,求出切线的方程.
2. 已知成本C与产量q的函数关系式为
,求当产量q=80时的边际成本.
布置作业布置作业
