导数的概念[上学期]
图片预览




文档简介
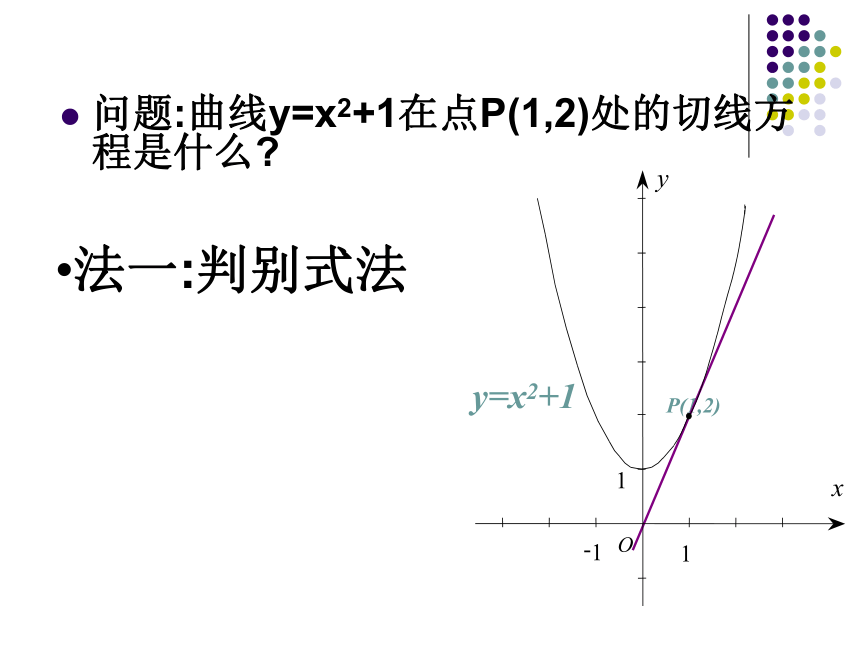
课件27张PPT。导数的概念引入问题:曲线y=x2+1在点P(1,2)处的切线方程是什么?
法一:判别式法
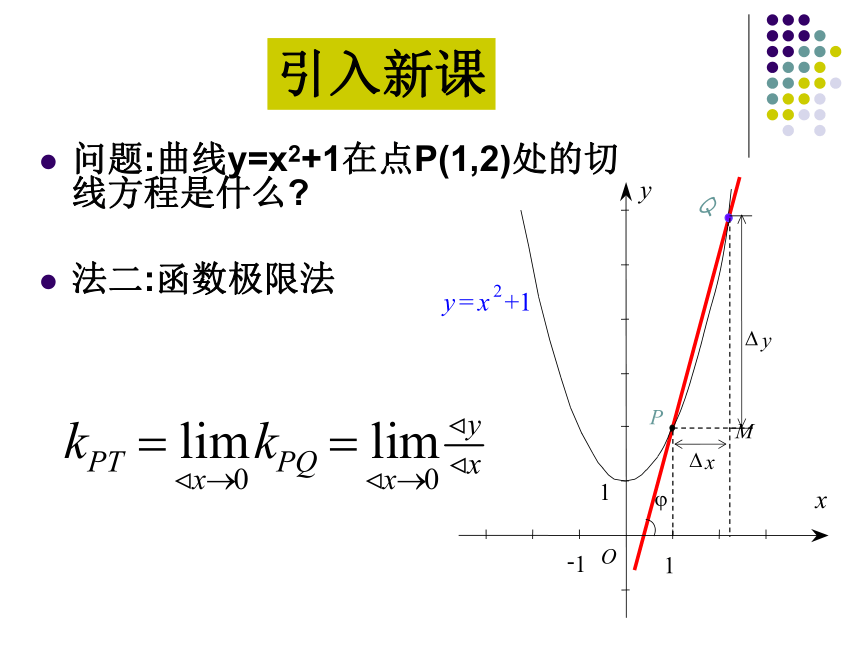
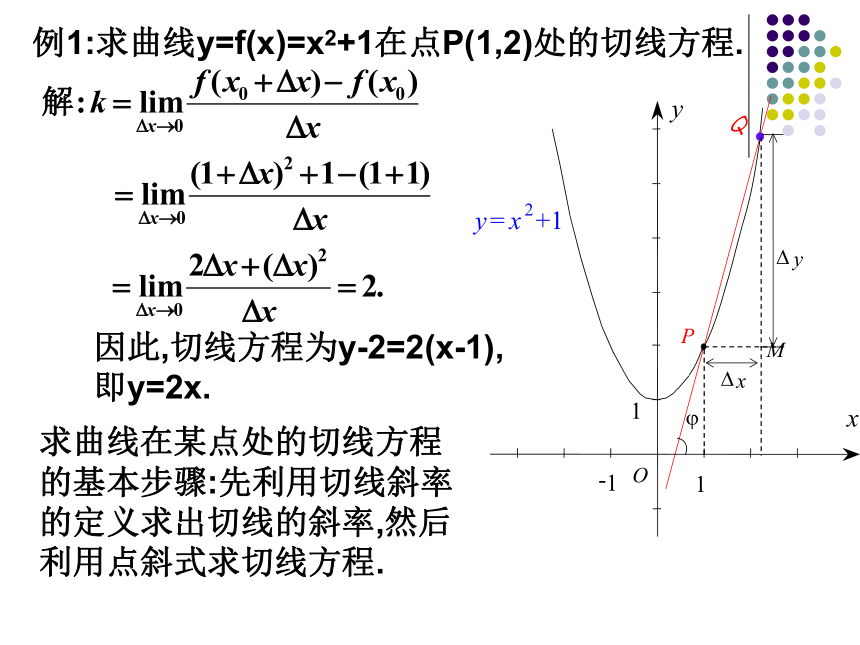
引入问题:曲线y=x2+1在点P(1,2)处的切线方程是什么?
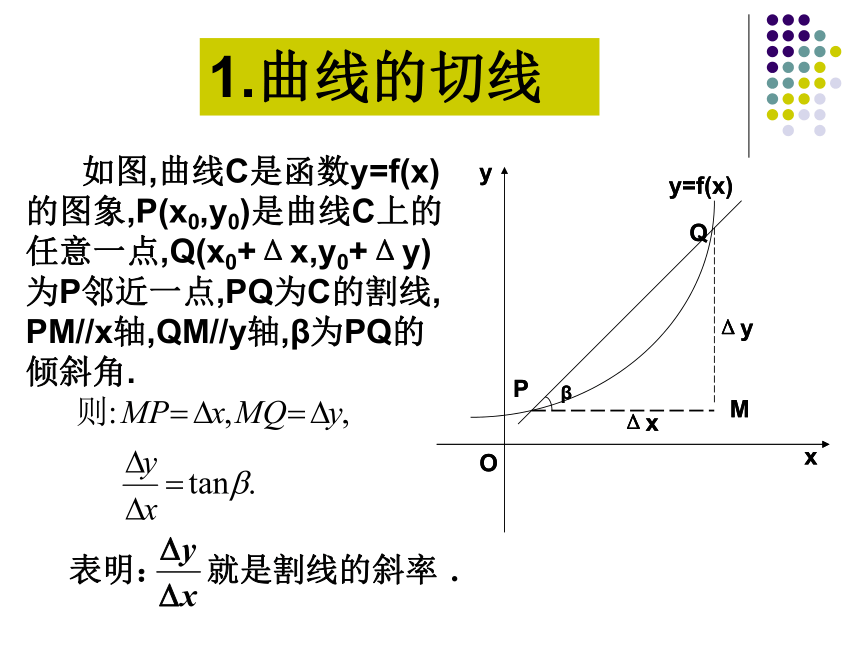
法二:函数极限法引入新课1.曲线的切线 如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.PQ割线切线T请看当
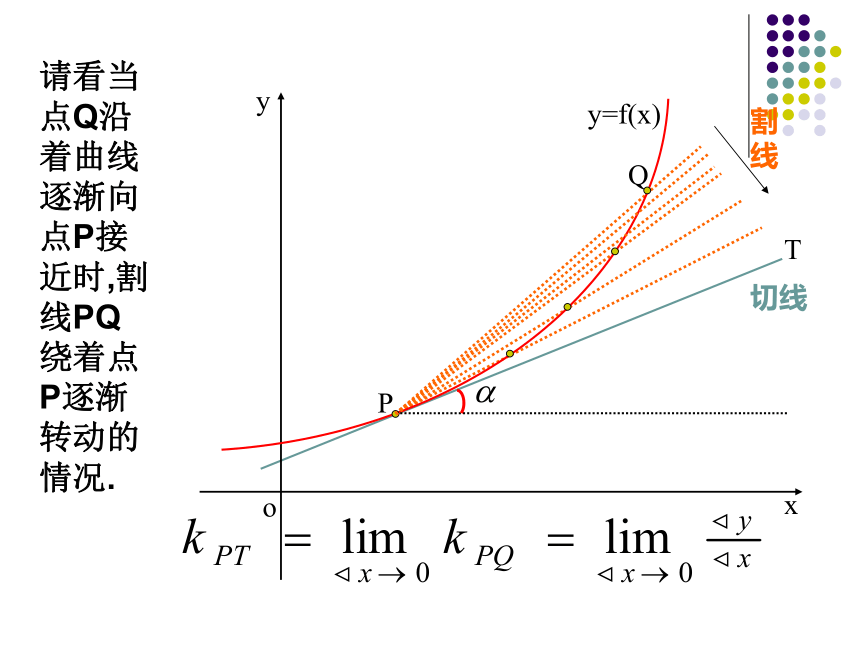
点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率. 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限. 要注意,曲线在某点处的切线:1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,
可以有多个,甚至可以无穷多个.因此,切线方程为y-2=2(x-1),
即y=2x.求曲线在某点处的切线方程
的基本步骤:先利用切线斜率
的定义求出切线的斜率,然后
利用点斜式求切线方程.故过点P的切线方程为:y-2=1?(x-1),即y=x+1.练习(1)求曲线 上一点P(2, )处的切线方程;
(2)求曲线 上一点P(1,-1)处的切线方程.答案:
12x-3y+16=0;
y=3x-4.求曲线的切线的斜率的一般步骤
(2)求割线的斜率:(3)求极限:(1)求函数值的增量 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t表示时间),求物体在t0时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Δt 的位置是s(t0+ Δ t)=OA1,则从t0 到 t0 +Δt 这段时间内,物体的位移是:在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
2.瞬时速度 平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也既需要通过瞬时速度来反映.2.瞬时速度即物体在时刻t0=2(s)的瞬时速度等于20(m/s).
当时间间隔Δt 逐渐变小时,平均速度就越接近t0=2(s) 时的瞬时速度v=20(m/s).2.瞬时速度练习:某质点沿直线运动,运动规律是s=5t2+6,求:
(1)2≤t≤2+Δt这段时间内的平均速度;
(2)当Δt=1时的平均速度;
(3)t=2时刻的瞬时速度.2.瞬时速度
(1)求位移增量 s=s(t+ t)-s(t)
求瞬时速度的步骤(2)求平均速度(3)求极限课堂小结:
(1)理解曲线的切线和物体运动的瞬时
速度都是用极限定义的.
(2) 求曲线上某点的切线的斜率.
(3)求物体运动的瞬时速度.提高练习:
1:已知曲线y=f(x)在点(x0,f(x0))处切线
的斜率为k,试求下列个极限的值.
完成创新方案P1848(切线斜率定义的应用)
法一:判别式法
引入问题:曲线y=x2+1在点P(1,2)处的切线方程是什么?
法二:函数极限法引入新课1.曲线的切线 如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.PQ割线切线T请看当
点Q沿着曲线逐渐向点P接近时,割线PQ绕着点P逐渐转动的情况.
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线. 设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率. 这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数平均变化率的极限. 要注意,曲线在某点处的切线:1)与该点的位置有关;
2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,
可以有多个,甚至可以无穷多个.因此,切线方程为y-2=2(x-1),
即y=2x.求曲线在某点处的切线方程
的基本步骤:先利用切线斜率
的定义求出切线的斜率,然后
利用点斜式求切线方程.故过点P的切线方程为:y-2=1?(x-1),即y=x+1.练习(1)求曲线 上一点P(2, )处的切线方程;
(2)求曲线 上一点P(1,-1)处的切线方程.答案:
12x-3y+16=0;
y=3x-4.求曲线的切线的斜率的一般步骤
(2)求割线的斜率:(3)求极限:(1)求函数值的增量 已知物体作变速直线运动,其运动方程为s=s(t)(s表示位移,t表示时间),求物体在t0时刻的速度. 如图设该物体在时刻t0的位置是s(t0)=OA0,在时刻t0 +Δt 的位置是s(t0+ Δ t)=OA1,则从t0 到 t0 +Δt 这段时间内,物体的位移是:在时间段( t0+Dt)- t0 = Dt 内,物体的平均速度为:
2.瞬时速度 平均速度反映了物体运动时的快慢程度,但要精确地描述非匀速直线运动,就要知道物体在每一时刻运动的快慢程度,也既需要通过瞬时速度来反映.2.瞬时速度即物体在时刻t0=2(s)的瞬时速度等于20(m/s).
当时间间隔Δt 逐渐变小时,平均速度就越接近t0=2(s) 时的瞬时速度v=20(m/s).2.瞬时速度练习:某质点沿直线运动,运动规律是s=5t2+6,求:
(1)2≤t≤2+Δt这段时间内的平均速度;
(2)当Δt=1时的平均速度;
(3)t=2时刻的瞬时速度.2.瞬时速度
(1)求位移增量 s=s(t+ t)-s(t)
求瞬时速度的步骤(2)求平均速度(3)求极限课堂小结:
(1)理解曲线的切线和物体运动的瞬时
速度都是用极限定义的.
(2) 求曲线上某点的切线的斜率.
(3)求物体运动的瞬时速度.提高练习:
1:已知曲线y=f(x)在点(x0,f(x0))处切线
的斜率为k,试求下列个极限的值.
完成创新方案P1848(切线斜率定义的应用)
