7.3 万有引力理论的成就(教学课件)-高中物理人教版(2019)必修第二册(共25张PPT)
文档属性
| 名称 | 7.3 万有引力理论的成就(教学课件)-高中物理人教版(2019)必修第二册(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-30 17:40:48 | ||
图片预览








文档简介
(共25张PPT)
第七章 万有引力与宇宙航行
第3节 万有引力理论的成就
问题与目标
1.通过对行星绕恒星运动、卫星运动的共同点和万有引力作为行星、卫星圆周运动的向心力的认识,学会用万有引力定律计算天体的质量和密度,掌握综合分析具体问题的方法。
2.通过查阅资料,了解万有引力定律在天文学上有重要应用。
3.通过了解地球表面物体的万有引力两个分力的大小关系,能计算地球质量。
回忆上节学习的万有引力定律的有关知识,回答一下问题:
1.万有引力定律的内容及公式是什么?
2.公式中的G又是什么?
3.G的测定有何重要意义?
天体之间的作用力主要是万有引力,引力常量的测出使万有引力定律有了实际意义。万有引力定律对天文学的发展起了很大的推动作用,揭示了天体运动的规律。这节课我们将举例来学习万有引力定律在天文学上的应用。
阅读教材55页右下角“蓝体字”部分和本页“问题”部分,想一想“地球的质量是多少?”这不可能用天平称量,但是可以通过万有引力定律来“称量”。
1.不考虑地球自转的影响,推导出地球质量的表达式,说明卡文迪什为什么能把自己的实验说成是“称量”地球的质量。
(一)“称量”地球的质量
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即: ,式中M是地球的质量,R是地球的半径,也就是物体到地心的距离。
根据关系式: ,由此关系式推导得出 (黄金代换式),从而可以求出地球的质量为:
地面的重力加速度g和地球半径R在卡文迪什之前就已知道,一旦测得引力常量G,就可以算出地球的质量M。
设地面附近的重力加速度g为9.8m/s2,地球半径R=6.4×106m,引力常量G=6.67×10-11N m2/kg2,试估算地球的质量。
小例题
根据刚才推导出的关系式计算:
所以说卡文迪什把他自己的实验说成是“称量”地球的重量,是不无道理的。
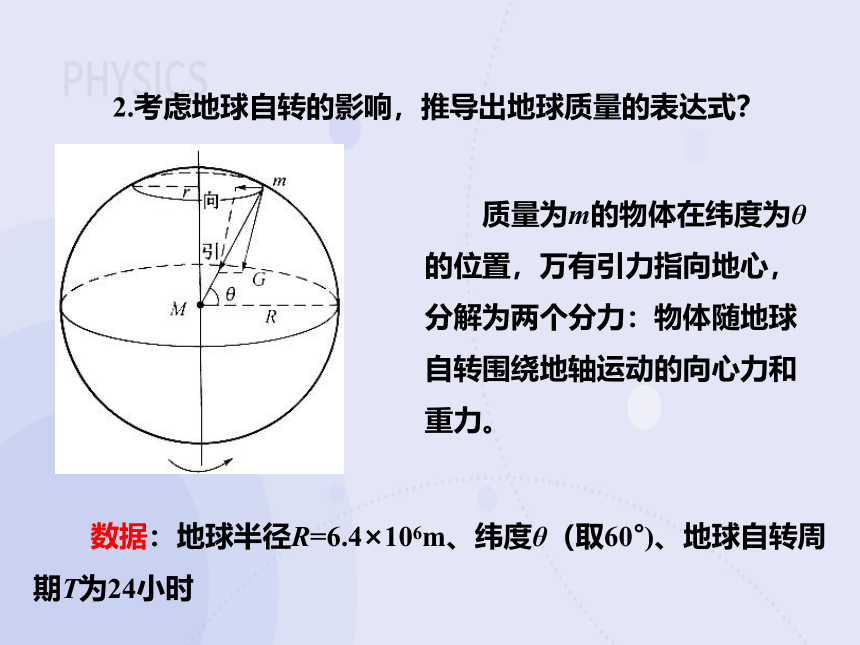
2.考虑地球自转的影响,推导出地球质量的表达式?
质量为m的物体在纬度为θ的位置,万有引力指向地心,分解为两个分力:物体随地球自转围绕地轴运动的向心力和重力。
数据:地球半径R=6.4×106m、纬度θ(取60°)、地球自转周期T为24小时
向心力远小于重力,万有引力大小近似等于重力。因此跟不考虑(忽略)地球自转的影响时得出结果一样, ,地球质量: 。
计算两个分力的大小比值,并做比较。
(二)计算天体的质量
用万有引力定律可算出地球的质量,能否算出太阳的质量是多少?行星做圆周运动的向心力的来源是什么?是否需要考虑九大行星之间的万有引力?
太阳质量远大于各个行星质量,高中阶段粗略计算,不考虑行星之间的万有引力。应用万有引力定律可以计算太阳等中心天体的质量。
1.中心天体质量计算的公式
设太阳的质量是M,某个行星的质量是m,r是行星与太阳之间的距离,ω是行星公转的角速度。按照刚才提出的思路,如何求出太阳的质量?
(1)根据万有引力提供行星绕太阳运动的向心力,有:
(2)行星的质量m在方程两侧被消去,所以只能求出中心天体的质量。将万有引力和右例向心加速度的不同表达式联立,得到中心天体质量的计算公式为:
(3)测出行星的公转周期T和它与太阳的距离r等,就可以算出太阳的质量。
从上面的学习可知,在应用万有引力定律求解天体质量时,只能求解中心天体的质量,而不能求解环绕天体的质量。而在求解中心天体质量的几种表达式中,最常用的是已知周期求质量的方程,因为环绕天体运动的周期比较容易测量。
(4)根据已知条件的不同,应选择不同的计算公式来计算中心天体的质量。对同一个中心天体,M是一个定值。所以: ,即在开普勒第三定律中,k是由中心天体的质量M决定的常量。
把地球绕太阳公转看作是匀速圆周运动,平均半径为1.5×1011m,已知引力常量为G=6.67×10-11N m2/kg2,则可估算出太阳的质量大约是多少千克?(结果取一位有效数字)
题干给出了轨道的半径,虽然没有给出地球运转的周期,但日常生活常识告诉我们:地球绕太阳一周约为365天。故:T=365×24×3600s=3.15×107s
由万有引力充当向心力可得:
故: ,
代入数据解得:
2.天体平均密度的计算
设中心天体的半径为R,平均密度为ρ,中心天体表面的重力加速度为g。行星或卫星的质量为m,轨道半径为r,线速度为v,角速度为ω,T为行星或卫星的运行周期。当行星或卫星环绕中心天体表面运行时,轨道半径r近似认为与中心天体的半径R相等。
(1)根据万有引力提供向心力有:
由上式可得中心天体平均密度的计算公式为:
(2)由上式还可得到一个有用的结论:对环绕任何中心天体表面的行星或卫星,有: 是一个普适常量。
3.星球表面附近的重力加速度
(1)重力及重力加速度与纬度的关系。
由于地球的自转,地面上的物体将随地球一起做匀速圆周运动。地球对地面物体的万有引力F的一个分力F1提供物体做圆周运动的向心力,另一个分力表现为物体的重力mg。所以除赤道和两极外,物体的重力并不严格指向地球的球心。同一物体的重力在赤道位置最小,两极处最大。导致赤道位置的重力加速度最小,随纬度位置的增加而逐渐增大,两极处最大。
①在两极位置:
②在赤道位置:
(2)重力加速度与高度的关系。
设中心天体的质量为M,半径为R。距星体表面高度为h处有一质量为m的物体。那么该处的重力加速度是多少?
物体在该处的重力等于星体对它的万有引力,该处的重力加速度为g′,则: ,所以: ,当h=0,物体在星球表面时, 。
(三)发现未知天体
考虑以下问题:
1.应用万有引力定律除可估算天体质量外,还可以在天文学上有何应用?
2.应用万有引力定律发现了哪些行星?
1.应用万有引力定律还可以用来发现未知的天体。
2.海王星、冥王星就是应用万有引力定律发现的。
(四)预言哈雷彗星回归
1.牛顿之前,彗星是一种神秘的现象。
2.哈雷的预言。
3.海王星的发现和哈雷彗星“按时回归”确立了万有引力定律的地位。
4.万有引力定律的作用:
(1)解释潮汐现象;
(2)推测出地球形状的产生原因;
(3)解释重力加速度的微小差别;
(4)解释重力探矿的原理;
(5)计算出宇宙速度。
课堂小练
B
A
D
A
第七章 万有引力与宇宙航行
第3节 万有引力理论的成就
问题与目标
1.通过对行星绕恒星运动、卫星运动的共同点和万有引力作为行星、卫星圆周运动的向心力的认识,学会用万有引力定律计算天体的质量和密度,掌握综合分析具体问题的方法。
2.通过查阅资料,了解万有引力定律在天文学上有重要应用。
3.通过了解地球表面物体的万有引力两个分力的大小关系,能计算地球质量。
回忆上节学习的万有引力定律的有关知识,回答一下问题:
1.万有引力定律的内容及公式是什么?
2.公式中的G又是什么?
3.G的测定有何重要意义?
天体之间的作用力主要是万有引力,引力常量的测出使万有引力定律有了实际意义。万有引力定律对天文学的发展起了很大的推动作用,揭示了天体运动的规律。这节课我们将举例来学习万有引力定律在天文学上的应用。
阅读教材55页右下角“蓝体字”部分和本页“问题”部分,想一想“地球的质量是多少?”这不可能用天平称量,但是可以通过万有引力定律来“称量”。
1.不考虑地球自转的影响,推导出地球质量的表达式,说明卡文迪什为什么能把自己的实验说成是“称量”地球的质量。
(一)“称量”地球的质量
若不考虑地球自转的影响,地面上质量为m的物体所受的重力mg等于地球对物体的引力,即: ,式中M是地球的质量,R是地球的半径,也就是物体到地心的距离。
根据关系式: ,由此关系式推导得出 (黄金代换式),从而可以求出地球的质量为:
地面的重力加速度g和地球半径R在卡文迪什之前就已知道,一旦测得引力常量G,就可以算出地球的质量M。
设地面附近的重力加速度g为9.8m/s2,地球半径R=6.4×106m,引力常量G=6.67×10-11N m2/kg2,试估算地球的质量。
小例题
根据刚才推导出的关系式计算:
所以说卡文迪什把他自己的实验说成是“称量”地球的重量,是不无道理的。
2.考虑地球自转的影响,推导出地球质量的表达式?
质量为m的物体在纬度为θ的位置,万有引力指向地心,分解为两个分力:物体随地球自转围绕地轴运动的向心力和重力。
数据:地球半径R=6.4×106m、纬度θ(取60°)、地球自转周期T为24小时
向心力远小于重力,万有引力大小近似等于重力。因此跟不考虑(忽略)地球自转的影响时得出结果一样, ,地球质量: 。
计算两个分力的大小比值,并做比较。
(二)计算天体的质量
用万有引力定律可算出地球的质量,能否算出太阳的质量是多少?行星做圆周运动的向心力的来源是什么?是否需要考虑九大行星之间的万有引力?
太阳质量远大于各个行星质量,高中阶段粗略计算,不考虑行星之间的万有引力。应用万有引力定律可以计算太阳等中心天体的质量。
1.中心天体质量计算的公式
设太阳的质量是M,某个行星的质量是m,r是行星与太阳之间的距离,ω是行星公转的角速度。按照刚才提出的思路,如何求出太阳的质量?
(1)根据万有引力提供行星绕太阳运动的向心力,有:
(2)行星的质量m在方程两侧被消去,所以只能求出中心天体的质量。将万有引力和右例向心加速度的不同表达式联立,得到中心天体质量的计算公式为:
(3)测出行星的公转周期T和它与太阳的距离r等,就可以算出太阳的质量。
从上面的学习可知,在应用万有引力定律求解天体质量时,只能求解中心天体的质量,而不能求解环绕天体的质量。而在求解中心天体质量的几种表达式中,最常用的是已知周期求质量的方程,因为环绕天体运动的周期比较容易测量。
(4)根据已知条件的不同,应选择不同的计算公式来计算中心天体的质量。对同一个中心天体,M是一个定值。所以: ,即在开普勒第三定律中,k是由中心天体的质量M决定的常量。
把地球绕太阳公转看作是匀速圆周运动,平均半径为1.5×1011m,已知引力常量为G=6.67×10-11N m2/kg2,则可估算出太阳的质量大约是多少千克?(结果取一位有效数字)
题干给出了轨道的半径,虽然没有给出地球运转的周期,但日常生活常识告诉我们:地球绕太阳一周约为365天。故:T=365×24×3600s=3.15×107s
由万有引力充当向心力可得:
故: ,
代入数据解得:
2.天体平均密度的计算
设中心天体的半径为R,平均密度为ρ,中心天体表面的重力加速度为g。行星或卫星的质量为m,轨道半径为r,线速度为v,角速度为ω,T为行星或卫星的运行周期。当行星或卫星环绕中心天体表面运行时,轨道半径r近似认为与中心天体的半径R相等。
(1)根据万有引力提供向心力有:
由上式可得中心天体平均密度的计算公式为:
(2)由上式还可得到一个有用的结论:对环绕任何中心天体表面的行星或卫星,有: 是一个普适常量。
3.星球表面附近的重力加速度
(1)重力及重力加速度与纬度的关系。
由于地球的自转,地面上的物体将随地球一起做匀速圆周运动。地球对地面物体的万有引力F的一个分力F1提供物体做圆周运动的向心力,另一个分力表现为物体的重力mg。所以除赤道和两极外,物体的重力并不严格指向地球的球心。同一物体的重力在赤道位置最小,两极处最大。导致赤道位置的重力加速度最小,随纬度位置的增加而逐渐增大,两极处最大。
①在两极位置:
②在赤道位置:
(2)重力加速度与高度的关系。
设中心天体的质量为M,半径为R。距星体表面高度为h处有一质量为m的物体。那么该处的重力加速度是多少?
物体在该处的重力等于星体对它的万有引力,该处的重力加速度为g′,则: ,所以: ,当h=0,物体在星球表面时, 。
(三)发现未知天体
考虑以下问题:
1.应用万有引力定律除可估算天体质量外,还可以在天文学上有何应用?
2.应用万有引力定律发现了哪些行星?
1.应用万有引力定律还可以用来发现未知的天体。
2.海王星、冥王星就是应用万有引力定律发现的。
(四)预言哈雷彗星回归
1.牛顿之前,彗星是一种神秘的现象。
2.哈雷的预言。
3.海王星的发现和哈雷彗星“按时回归”确立了万有引力定律的地位。
4.万有引力定律的作用:
(1)解释潮汐现象;
(2)推测出地球形状的产生原因;
(3)解释重力加速度的微小差别;
(4)解释重力探矿的原理;
(5)计算出宇宙速度。
课堂小练
B
A
D
A
