导数的概念[上学期]

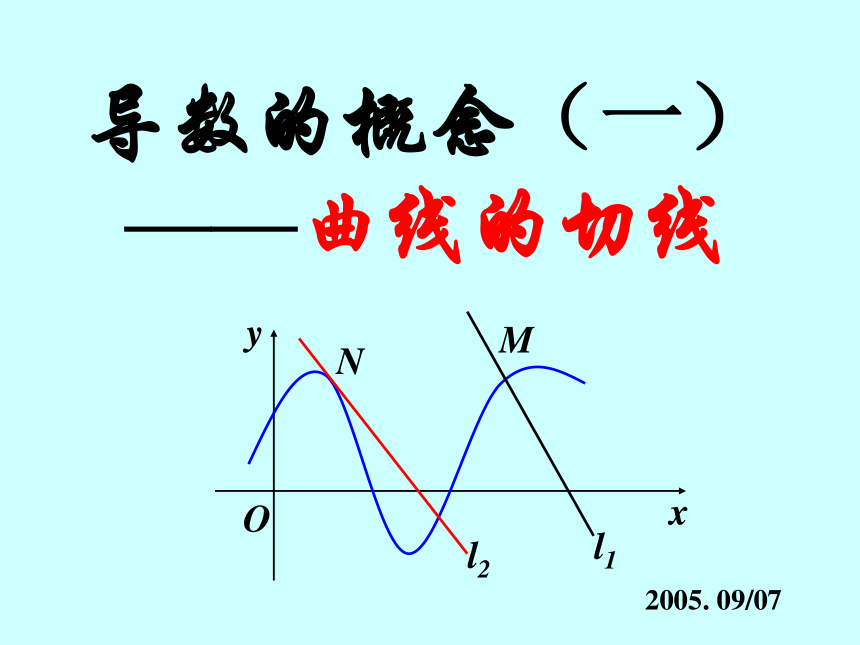
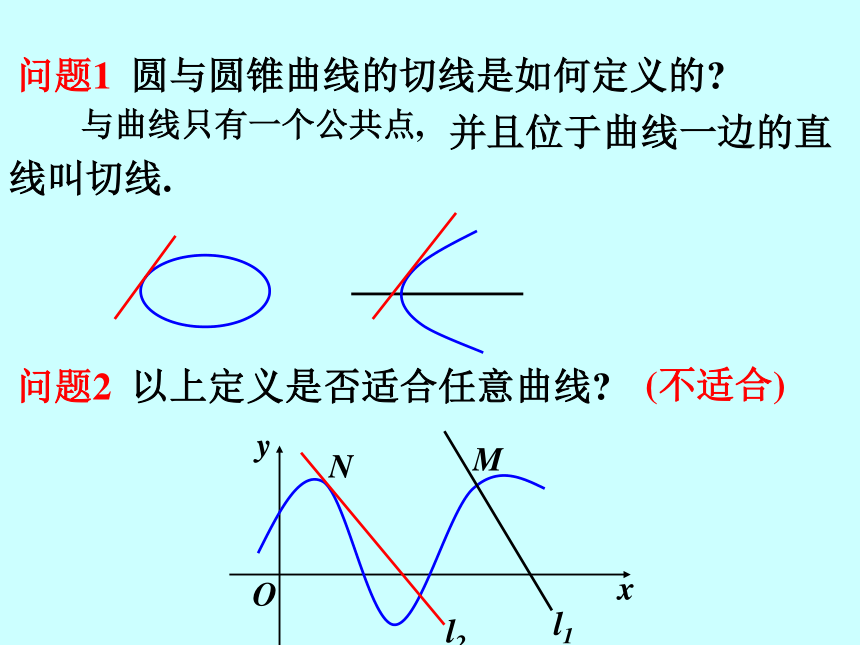
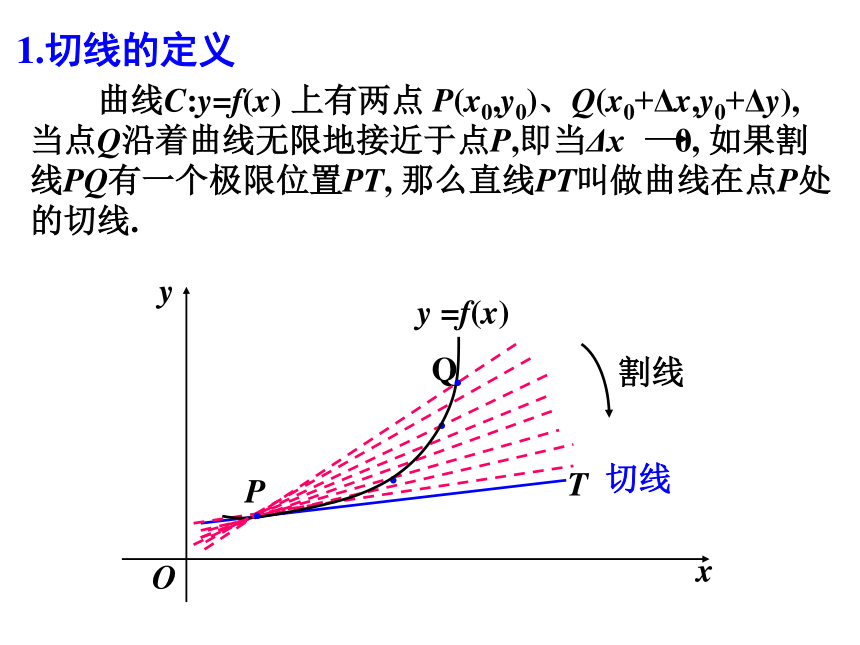
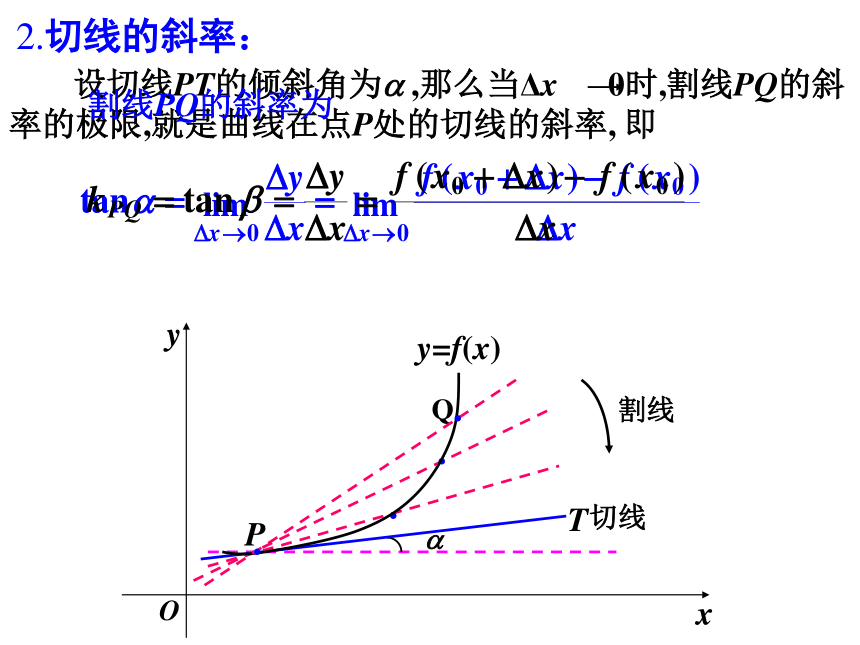
课件20张PPT。导数的概念（一） ——曲线的切线2005. 09/07问题1 圆与圆锥曲线的切线是如何定义的?与曲线只有一个公共点, 并且位于曲线一边的直线叫切线.问题2 以上定义是否适合任意曲线?(不适合)问题1、2MΔxΔy 问题3:如图函数y=f(x)的图象,其上有两点 P(x0, y0) 、Q(x0+Δx, y0+Δy), 则过点P、Q作割线PQ的斜率是多少？问题3 曲线C:y=f(x) 上有两点 P(x0,y0)、Q(x0+Δx,y0+Δy), 当点Q沿着曲线无限地接近于点P,即当Δx 0, 如果割线PQ有一个极限位置PT, 那么直线PT叫做曲线在点P处的切线.Q1.切线的定义切线的定义切线2.切线的斜率：切线的斜率练习: y=x3在P处的切线斜率为3, 求点P的坐标. 解: 设点P的坐标为(x0, y0), 则过点P 的切线的斜率为 又知k=3, ∴ 3x02=3 即x0=±1　 当x0=1时, y0=13=1; 当x0= –1时, y0=(–1)3= –1，所求点P的坐标为(1,1)或(–1, –1)补例——瞬时速度导数的概念（二）
物体自由落体的运动方程是 ，其中位
移单位是m，时间单位是s， ．怎样求物体在
这一时刻的速度呢？
一、实例分析二、尝试发现
右图的曲线为
的函数曲线，M点是 时所对应的点，设N点所对应 t 的值为1s，请同学们求一下物体在1s到3s 这段时间时内的平均速度？
这个平均速度显然代替不了M点的瞬时速度，请同学们再计算一下2s到3s这段时间内的平均速度，2.9s到3s这段时间内的平均速度，及2.99s到3s这段时间内的平均速度. 设M点所对应的时刻为 ， 取不同值时的平均速度为 则：
在这里体现了极限的思想，也就是说在
这一时刻的瞬时速度等于在 到 这段时间内的平均速度当 的极限， 即

?
设物体的运动方程是 , 物体在时刻 的瞬时速度为 , 就是物体在 到 这段时间内,当
时平均速度的极限 ，即 导数的概念曲线的切线斜率公式: 物体的瞬时速度及切线的斜率都是函数的改变量 与自变量的改变量 之比的极限 ． 二者共同的数学结构为：定义：设函数y=f(x)在点x0处及其附近有定义，当自变量x在点x0处有改变量Dx时，函数y相应的 增量 Dy= f(x0+ Dx) － f(x0)2．引入新课 —— 导数的概念 〖例１〗求 在 点处的导数． P109 练习 1、2函数 y=f(x)在点x0处的导数的几何意义，就是曲线 y=f(x) 在点P(x0 ,f(x0)) 处的切线的斜率。曲线 y=f(x)在点P(x0 ，f(x0))处的切线斜率是f ′(x0)4. 导数的几何意义切线方程是例2 、如图，已知曲线
(1)点P处的切线的斜率.
(2)点P处的切线的方程.