苏科版八年级上册4.3实数 课件(共20张PPT)
文档属性
| 名称 | 苏科版八年级上册4.3实数 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-31 07:43:31 | ||
图片预览







文档简介
(共20张PPT)
实 数
知识建构:数的扩充
x+5=2 3x=2 x2=2 x是自然数 x是整数 x是整数 x是有理数 x是有理数 x是实数
根据给定的范围,求下面几个方程的解.
自然数
整数
有理数
实数
负数
减法的需要
分数
除法的需要
无理数
开方的需要
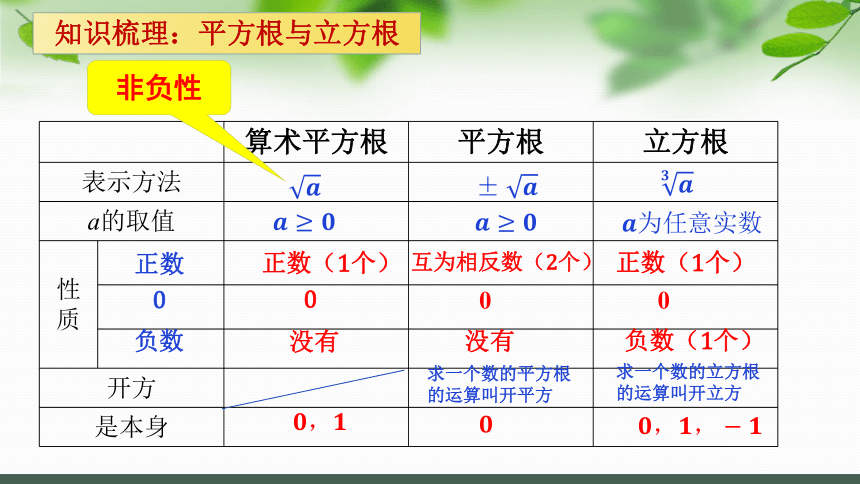
算术平方根 平方根 立方根
表示方法
a的取值
性 质
开方
是本身
为任意实数
正数
正数(1个)
互为相反数(2个)
正数(1个)
0
0
0
0
负数
没有
没有
负数(1个)
非负性
知识梳理:平方根与立方根
求一个数的立方根的运算叫开立方
求一个数的平方根的运算叫开平方
填一填,想一想:
=
=
=
=
=
知识梳理:平方根与立方根
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
无限不循环小数
可以写成,
含有π的数;
开方开不尽的数;
无限不循环小数.
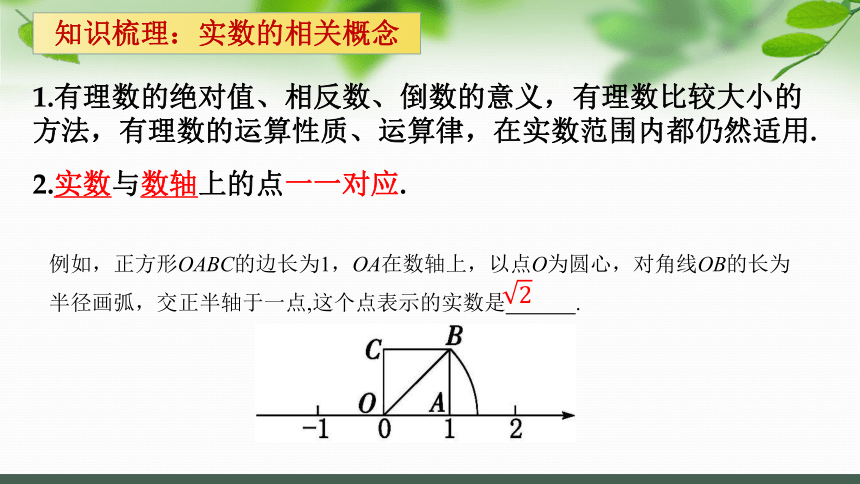
知识梳理:实数的相关概念
整数、分数、有限小数、无限循环小数
2.实数与数轴上的点一一对应.
1.有理数的绝对值、相反数、倒数的意义,有理数比较大小的方法,有理数的运算性质、运算律,在实数范围内都仍然适用.
知识梳理:实数的相关概念
例如,正方形OABC的边长为1,OA在数轴上,以点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,这个点表示的实数是 .
小明的体重约为51.51kg,
如果精确到10kg,那么小明的体重约为 50 kg;
如果精确到1kg,那么小明的体重约为 52 kg;
如果精确到0.1kg,那么小明的体重约为 51.5 kg.
一个近似数四舍五入到哪一位,那么这个近似数精确到哪一位.
知识梳理:近似数
热身练习
1. 下列说法,正确的有: .
①实数和数轴上的点是一一对应的;
②无理数是开方开不尽的数;
③负数没有立方根;
④16的平方根是±4,用式子表示是
⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0.
2. 有下列实数:,其中无理数有: .
3. 将67294精确到万位是 7×104 (用科学记数法表示),0.0610精确到 万分 位.
①⑤
4.计算:
3
2
去绝对值添括号
热身练习
5. 解方程:
(2)
整体思想
热身练习
例1.已知数 a 的平方根是 m+1 和 2m-7 ,则m = ,a = .
变式:一个正数a的两个平方根是2b-1和b+4,a+b的立方根为 .
典型例题
2
9
2
典型例题
例2. 估计
A.在4和5之间 B.在3和4之间 C.在2和3之间 D.在1和2之间
变式:若的整数部分为a,的整数部分为b,则a+b的值为 .
无理数的估算:借助一些数的平方,用有理数逼近无理数。
A
5
例3.已知,则下列大小关系正确的是( )
A. B. C D.
典型例题
变式:若,则大小关是( )
A. B. C D.
实数比较大小常用方法:数轴法、求差法、求商法、绝对值比较法、平方法
A
A
典型例题
例4. 若x、y都是实数,且,求x+3y的立方根.
实数的三个非负性:
几个非负数之和等于0,则每个非负数都等于0.
变式:已知求2a3b的平方根.
例5. 如图,数轴上A、B两点表示的数分别为,点B关于点A的对称点C,则点C所表示的数是 .
典型例题
A
B
0
变式: 如图,数轴上表示的对应点分别为点A、点B,若点A是BC的中点,则点C所表示的数是 .
A
C
2
0
B
实数与数轴上点一一对应:
利用数轴上的点对应的实数表示两点之间的距离及对称的性质.
数形结合
典型例题
例6. 实数在数轴上的位置如图所示,化简.
0
a
b
结合数轴,判断符号,利用平方根的性质()、绝对值的性质进行化简.
典型例题
变式:实数在数轴上的对应点位置如图所示,
化简.
b
a
0
c
立方根
有理数
无理数
实数
算术平方根
负的平方根
平方根
开方
乘方
逆运算
开平方
开立方
课堂小结
1.实数与数轴上的点一一对应.
2.实数大小比较常用方法:数轴法、求差法、求商法、绝对值比较法、平方法.
平方根的性质:非负性、
整体思想
数形结合
x+5=2 3x=2 x2=2 x是自然数 x是整数 x是整数 x是有理数 x是有理数 x是实数
无解
无解
无解
根据给定的范围,求下面几个方程的解.
自然数
整数
有理数
实数
负数
减法的需要
分数
除法的需要
无理数
开方的需要
学习展望
x2=2
x是实数
?
?
同学们再见!
实 数
知识建构:数的扩充
x+5=2 3x=2 x2=2 x是自然数 x是整数 x是整数 x是有理数 x是有理数 x是实数
根据给定的范围,求下面几个方程的解.
自然数
整数
有理数
实数
负数
减法的需要
分数
除法的需要
无理数
开方的需要
算术平方根 平方根 立方根
表示方法
a的取值
性 质
开方
是本身
为任意实数
正数
正数(1个)
互为相反数(2个)
正数(1个)
0
0
0
0
负数
没有
没有
负数(1个)
非负性
知识梳理:平方根与立方根
求一个数的立方根的运算叫开立方
求一个数的平方根的运算叫开平方
填一填,想一想:
=
=
=
=
=
知识梳理:平方根与立方根
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
无限不循环小数
可以写成,
含有π的数;
开方开不尽的数;
无限不循环小数.
知识梳理:实数的相关概念
整数、分数、有限小数、无限循环小数
2.实数与数轴上的点一一对应.
1.有理数的绝对值、相反数、倒数的意义,有理数比较大小的方法,有理数的运算性质、运算律,在实数范围内都仍然适用.
知识梳理:实数的相关概念
例如,正方形OABC的边长为1,OA在数轴上,以点O为圆心,对角线OB的长为半径画弧,交正半轴于一点,这个点表示的实数是 .
小明的体重约为51.51kg,
如果精确到10kg,那么小明的体重约为 50 kg;
如果精确到1kg,那么小明的体重约为 52 kg;
如果精确到0.1kg,那么小明的体重约为 51.5 kg.
一个近似数四舍五入到哪一位,那么这个近似数精确到哪一位.
知识梳理:近似数
热身练习
1. 下列说法,正确的有: .
①实数和数轴上的点是一一对应的;
②无理数是开方开不尽的数;
③负数没有立方根;
④16的平方根是±4,用式子表示是
⑤某数的绝对值,相反数,算术平方根都是它本身,则这个数是0.
2. 有下列实数:,其中无理数有: .
3. 将67294精确到万位是 7×104 (用科学记数法表示),0.0610精确到 万分 位.
①⑤
4.计算:
3
2
去绝对值添括号
热身练习
5. 解方程:
(2)
整体思想
热身练习
例1.已知数 a 的平方根是 m+1 和 2m-7 ,则m = ,a = .
变式:一个正数a的两个平方根是2b-1和b+4,a+b的立方根为 .
典型例题
2
9
2
典型例题
例2. 估计
A.在4和5之间 B.在3和4之间 C.在2和3之间 D.在1和2之间
变式:若的整数部分为a,的整数部分为b,则a+b的值为 .
无理数的估算:借助一些数的平方,用有理数逼近无理数。
A
5
例3.已知,则下列大小关系正确的是( )
A. B. C D.
典型例题
变式:若,则大小关是( )
A. B. C D.
实数比较大小常用方法:数轴法、求差法、求商法、绝对值比较法、平方法
A
A
典型例题
例4. 若x、y都是实数,且,求x+3y的立方根.
实数的三个非负性:
几个非负数之和等于0,则每个非负数都等于0.
变式:已知求2a3b的平方根.
例5. 如图,数轴上A、B两点表示的数分别为,点B关于点A的对称点C,则点C所表示的数是 .
典型例题
A
B
0
变式: 如图,数轴上表示的对应点分别为点A、点B,若点A是BC的中点,则点C所表示的数是 .
A
C
2
0
B
实数与数轴上点一一对应:
利用数轴上的点对应的实数表示两点之间的距离及对称的性质.
数形结合
典型例题
例6. 实数在数轴上的位置如图所示,化简.
0
a
b
结合数轴,判断符号,利用平方根的性质()、绝对值的性质进行化简.
典型例题
变式:实数在数轴上的对应点位置如图所示,
化简.
b
a
0
c
立方根
有理数
无理数
实数
算术平方根
负的平方根
平方根
开方
乘方
逆运算
开平方
开立方
课堂小结
1.实数与数轴上的点一一对应.
2.实数大小比较常用方法:数轴法、求差法、求商法、绝对值比较法、平方法.
平方根的性质:非负性、
整体思想
数形结合
x+5=2 3x=2 x2=2 x是自然数 x是整数 x是整数 x是有理数 x是有理数 x是实数
无解
无解
无解
根据给定的范围,求下面几个方程的解.
自然数
整数
有理数
实数
负数
减法的需要
分数
除法的需要
无理数
开方的需要
学习展望
x2=2
x是实数
?
?
同学们再见!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
