5.3.1 平行线的性质 课件(共22张PPT)
文档属性
| 名称 | 5.3.1 平行线的性质 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-01 18:29:10 | ||
图片预览






文档简介
(共22张PPT)
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
学习目标
1.掌握平行线的三个性质定理.
2.能够灵活运用平行线的三个性质定理进行简单的推理和计算.
3.综合运用平行线的判定与性质进行简单的证明或计算.
重点:平行线的三个性质定理的理解与简单应用.
难点:正确使用推理的基本格式.
课前预习
互补
相等
相等
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新课导入
知识点
平行线
两条平行线被第三条直线截得的同位角具有怎样的数量关系?
思考
探究新知
如图,已知直线 a∥b ,c 是截线.
b
a
c
1
2
3
4
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
探究
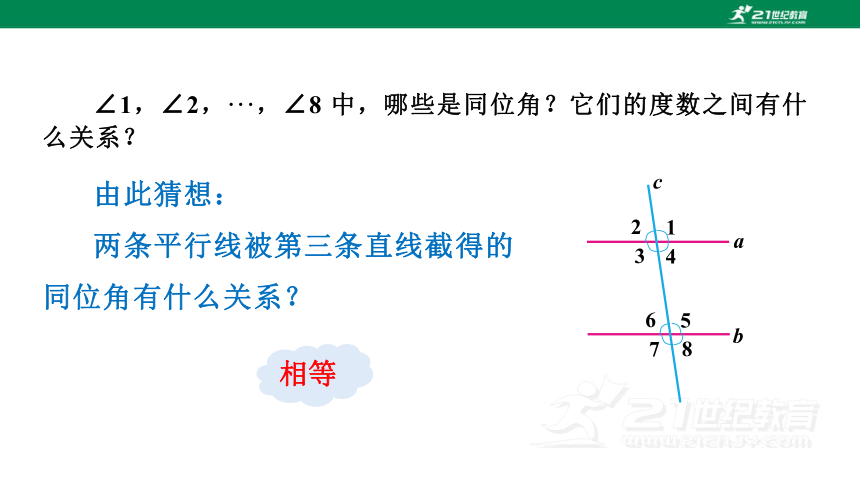
∠1,∠2,···,∠8 中,哪些是同位角?它们的度数之间有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
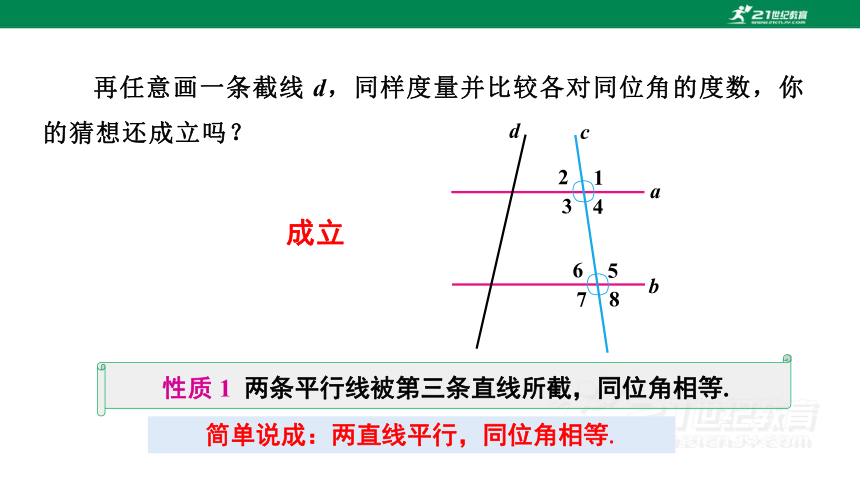
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质 1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
如图,直线 a∥b ,c 是截线,那么 1 与 2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质 2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质 3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
知识归纳
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A 与∠D 互补,∠B与∠C 互补.
例题分析
于是∠D = 180 ° -∠A
= 180 ° -100 = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是 80 ° ,65°.
例2
如图,已知DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,
∴∠CAG=∠ACE=36°,
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
例题分析
例3 如图,已知AB∥CD,直线EF分别交AB,CD于点M,N,MP平分∠EMA,NQ平分∠MNC,那么MP∥NQ,为什么?
解:∵AB∥CD,
∴∠EMA=∠MNC.
∵MP平分∠EMA,NQ平分∠MNC,∴∠EMP= ∠EMA,∠MNQ= ∠MNC,∴∠EMP=∠MNQ,∴MP∥NQ.
例题分析
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
课堂练习
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,
∴∠C = ∠AED = 40°(两直线平行,同位角相等)
3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
B
4.如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
5.如图,CD⊥AB于点D,E是BC上一点,EF⊥AB于点F,∠1=∠2,试说明∠AGD=∠ACB的理由.
解:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,∴∠AGD=∠ACB.
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
1.教材P22~23习题5.3第1,2,3,6题;
2.完成对应课时练习.
布置作业
第五章 相交线与平行线
5.3 平行线的性质
5.3.1 平行线的性质
学习目标
1.掌握平行线的三个性质定理.
2.能够灵活运用平行线的三个性质定理进行简单的推理和计算.
3.综合运用平行线的判定与性质进行简单的证明或计算.
重点:平行线的三个性质定理的理解与简单应用.
难点:正确使用推理的基本格式.
课前预习
互补
相等
相等
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
想一想: 平行线的三种判定方法分别是
先知道什么……、 后知道什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
新课导入
知识点
平行线
两条平行线被第三条直线截得的同位角具有怎样的数量关系?
思考
探究新知
如图,已知直线 a∥b ,c 是截线.
b
a
c
1
2
3
4
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
100°
80°
100°
80°
100°
80°
100°
80°
探究
∠1,∠2,···,∠8 中,哪些是同位角?它们的度数之间有什么关系?
由此猜想:
两条平行线被第三条直线截得的同位角有什么关系?
相等
b
a
c
1
2
3
4
5
6
7
8
再任意画一条截线 d,同样度量并比较各对同位角的度数,你的猜想还成立吗?
b
a
c
1
2
3
4
5
6
7
8
d
成立
性质 1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
思考
如图,直线 a∥b ,c 是截线,那么 1 与 2 相等吗?为什么?
根据“两直线平行,同位角相等”,可得∠2 = ∠3 .
而∠3 与∠1 互为对顶角,所以∠3 =∠1.
所以∠1 = ∠2.
b
a
c
3
2
1
性质 2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
性质 3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
类似地,
平行线的性质:
性质1:两直线平行,同位角相等;
性质2:两直线平行,内错角相等;
性质3:两直线平行,同旁内角互补.
知识归纳
例1 如图,是一块梯形铁片的残余部分,量得∠A = 100 ° ,∠B = 115 ° ,梯形的另外两个角分别是多少度?
解:因为梯形上、下两底 AB∥CD ,根据“两直线平行,同旁内角互补”,可得∠A 与∠D 互补,∠B与∠C 互补.
例题分析
于是∠D = 180 ° -∠A
= 180 ° -100 = 80 ° ,
∠C = 180 ° -∠B
= 180 ° -115 ° = 65 ° .
所以,梯形的另外两个角分别是 80 ° ,65°.
例2
如图,已知DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,
∴∠CAG=∠ACE=36°,
∴∠PAC=∠CAG+∠PAG=36°+12°=48°.
∵AP平分∠BAC,
∴∠BAP=∠PAC=48°.
∵DB∥FG,
∴∠ABD=∠BAG=∠BAP+∠PAG=48°+12°=60°.
例题分析
例3 如图,已知AB∥CD,直线EF分别交AB,CD于点M,N,MP平分∠EMA,NQ平分∠MNC,那么MP∥NQ,为什么?
解:∵AB∥CD,
∴∠EMA=∠MNC.
∵MP平分∠EMA,NQ平分∠MNC,∴∠EMP= ∠EMA,∠MNQ= ∠MNC,∴∠EMP=∠MNQ,∴MP∥NQ.
例题分析
1. 如图,直线 a∥b,∠1 = 54°,∠2,∠3,∠4 各是多少度?
解:∵a∥b,∠1=54°,∴∠4 =∠1 = 54°(两直线平行,同位角相等).
∠3 =180°-∠4
=180° - 54°=126°,
∠2 与∠1 是对顶角,
∴∠2=∠1= 54°.
课堂练习
2. 如图,在△ABC 中,D 是 AB 上一点,E 是 AC 上一点, ∠ADE = 60°,∠B = 60°,∠AED = 40°.
(1)DE 与 BC 平行吗?为什么?
(2)∠C 是多少度?为什么?
解:(1)∵∠ADE = ∠B,∴DE∥BC(同位角相等,两直线平行)
(2)∵DE∥BC,
∴∠C = ∠AED = 40°(两直线平行,同位角相等)
3.下列图形中,根据AB∥CD,能得到∠1=∠2的是( )
B
4.如图,若∠1+∠2=180°,∠3=110°,则∠4=_______.
110°
5.如图,CD⊥AB于点D,E是BC上一点,EF⊥AB于点F,∠1=∠2,试说明∠AGD=∠ACB的理由.
解:∵CD⊥AB,EF⊥AB,
∴∠EFB=∠CDB=90°,
∴CD∥EF,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=∠3,
∴DG∥BC,∴∠AGD=∠ACB.
图形 已知 结果 理由
a∥b ∠1=∠3
∠2=∠4
a∥b 两直线平行,同旁内角互补
两直线平行,同位角相等
a∥b
两直线平行,内错角相等
∠2+∠3=180°
b
a
c
1
2
3
4
课堂小结
1.教材P22~23习题5.3第1,2,3,6题;
2.完成对应课时练习.
布置作业
