华东师大版数学九年级上册23.3.3《相似三角形的性质》课时练习 (含答案)
文档属性
| 名称 | 华东师大版数学九年级上册23.3.3《相似三角形的性质》课时练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 154.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-31 00:00:00 | ||
图片预览


文档简介
2022-2023年华师大版数学九年级上册23.3.3
《相似三角形的性质》课时练习
一 、选择题
1.如图,在△ABC 中,∠C=90°,D 是 AC 上一点,DE⊥AB 于点 E,若 AC=8,BC=6,DE=3,则 AD 的长为( )
A.3 B.4 C.5 D.6
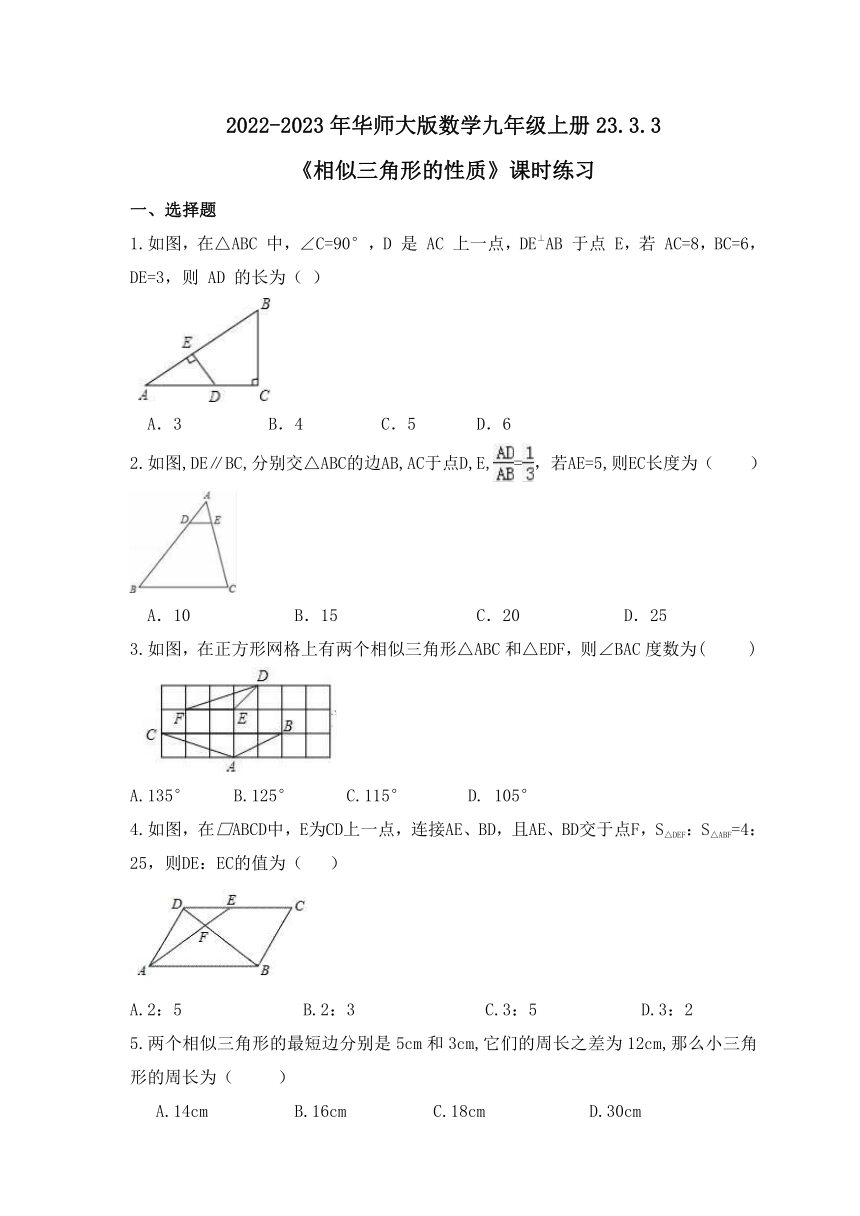
2.如图,DE∥BC,分别交△ABC的边AB,AC于点D,E,=,若AE=5,则EC长度为( )
A.10 B.15 C.20 D.25
3.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠BAC度数为( )
A.135° B.125° C.115° D. 105°
4.如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC的值为( )
A.2:5 B.2:3 C.3:5 D.3:2
5.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
6.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
7.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )
A.4 B.6 C.8 D.不能确定
8.如图,在 ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF∶FC等于( )
A.1∶4 B.1∶3 C.2∶3 D.1∶2
9.如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
A.64 B.72 C.80 D.96
10.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,
若S△DOE∶S△COA=1∶25,则BE∶CE=( )
A.1∶3 B.1∶4 C.1∶5 D.1∶25
二 、填空题
11.若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
12.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为 ,面积为 .
13.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为 .
14.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比是________.
15.如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN= ;
16.如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为 .
三 、解答题
17.一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
18.已知△ABC∽△A′B′C′,=,AB边上的中线CD=4 cm,△ABC的周长为20 cm,△A′B′C′的面积是64 cm2,求:
(1)A′B′边上的中线C′D′的长;
(2)△A′B′C′的周长;
(3)△ABC的面积.
19.如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED=∠B.若AE=5,AB=9,CB=6,求ED的长.
20.如图,在△ABC中,AB=6cm,AC=12cm,动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t, 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
21.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= °.
(2)如图,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
参考答案
1.C
2.A
3.A
4.B
5.C
6.B.
7.C.
8.D
9.C
10.B
11.答案为:5:4.
12.答案为:90,270.
13.答案为:6;
14.答案为:1:9
15.答案为:3-;
16.答案为:2.5.
17.解:设另一个三角形的两边长是xcm,ycm,由题意,得:
x:5=y:8=4.8:12,
解得x=2cm,y=3.2cm.
因此另两条边的边长为2cm,3.2cm.
18.解:(1)8 cm (2)40 cm (3)16 cm2
19.解:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,
∴=,
∵AE=5,AB=9,CB=6,
∴=,解得DE=
20.解:存在t=3秒或4.8秒,使以点A、M、N为顶点的三角形与△ABC相似
设经过t秒时,△AMN与△ABC相似,
此时,AM=t , CN=2t , AN=12-2t(0≤t≤6),
①当MN∥BC时,△AMN∽△ABC ,
则 = ,即 = ,解得t=3;
②当∠AMN=∠C时,△ANM∽△ABC ,
则 = ,即 = ,解得t=4.8;
故所求t的值为3秒或4.8秒.
21.解:(1)当AD=CD时,如图,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知AC=AD=2,
∵△BCD∽△BAC,
∴=,
设BD=x,
∴()2=x(x+2),
∵x>0,
∴x=﹣1,
∵△BCD∽△BAC,
∴==
《相似三角形的性质》课时练习
一 、选择题
1.如图,在△ABC 中,∠C=90°,D 是 AC 上一点,DE⊥AB 于点 E,若 AC=8,BC=6,DE=3,则 AD 的长为( )
A.3 B.4 C.5 D.6
2.如图,DE∥BC,分别交△ABC的边AB,AC于点D,E,=,若AE=5,则EC长度为( )
A.10 B.15 C.20 D.25
3.如图,在正方形网格上有两个相似三角形△ABC和△EDF,则∠BAC度数为( )
A.135° B.125° C.115° D. 105°
4.如图,在□ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC的值为( )
A.2:5 B.2:3 C.3:5 D.3:2
5.两个相似三角形的最短边分别是5cm和3cm,它们的周长之差为12cm,那么小三角形的周长为( )
A.14cm B.16cm C.18cm D.30cm
6.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为,则下列结论中正确的是( )
A.m=5 B.m=4 C.m=3 D.m=10
7.如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=2,则S1+S2=( )
A.4 B.6 C.8 D.不能确定
8.如图,在 ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF∶FC等于( )
A.1∶4 B.1∶3 C.2∶3 D.1∶2
9.如图,在△ABC中,D,E分别是边AB,BC上的点,且DE∥AC,若S△BDE=4,S△CDE=16,则△ACD的面积为( )
A.64 B.72 C.80 D.96
10.如图,D,E分别是△ABC的边AB,BC上的点,且DE∥AC,AE,CD相交于点O,
若S△DOE∶S△COA=1∶25,则BE∶CE=( )
A.1∶3 B.1∶4 C.1∶5 D.1∶25
二 、填空题
11.若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为 .
12.如果一个三角形的三边长为5、12、13,与其相似的三角形的最长的边为39,那么较大的三角形的周长为 ,面积为 .
13.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则AC的长为 .
14.如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比是________.
15.如图,正五边形的边长为2,连对角线AD,BE,CE,线段AD分别与BE和CE相交于点M,N,则MN= ;
16.如图,在 ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为 .
三 、解答题
17.一个三角形三边长分别为5cm,8cm,12cm,另一个与它相似的三角形的最长边为4.8cm,求另外两边长.
18.已知△ABC∽△A′B′C′,=,AB边上的中线CD=4 cm,△ABC的周长为20 cm,△A′B′C′的面积是64 cm2,求:
(1)A′B′边上的中线C′D′的长;
(2)△A′B′C′的周长;
(3)△ABC的面积.
19.如图,在△ABC中,D,E分别是AB,AC上一点,且∠AED=∠B.若AE=5,AB=9,CB=6,求ED的长.
20.如图,在△ABC中,AB=6cm,AC=12cm,动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t, 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
21.从三角形(不是等腰三角形)一个顶点引起一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)在△ABC中,∠A=48°,CD是△ABC的完美分割线,且AD=CD,则∠ACB= °.
(2)如图,在△ABC中,AC=2,BC=,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
参考答案
1.C
2.A
3.A
4.B
5.C
6.B.
7.C.
8.D
9.C
10.B
11.答案为:5:4.
12.答案为:90,270.
13.答案为:6;
14.答案为:1:9
15.答案为:3-;
16.答案为:2.5.
17.解:设另一个三角形的两边长是xcm,ycm,由题意,得:
x:5=y:8=4.8:12,
解得x=2cm,y=3.2cm.
因此另两条边的边长为2cm,3.2cm.
18.解:(1)8 cm (2)40 cm (3)16 cm2
19.解:∵∠AED=∠B,∠A=∠A,
∴△AED∽△ABC,
∴=,
∵AE=5,AB=9,CB=6,
∴=,解得DE=
20.解:存在t=3秒或4.8秒,使以点A、M、N为顶点的三角形与△ABC相似
设经过t秒时,△AMN与△ABC相似,
此时,AM=t , CN=2t , AN=12-2t(0≤t≤6),
①当MN∥BC时,△AMN∽△ABC ,
则 = ,即 = ,解得t=3;
②当∠AMN=∠C时,△ANM∽△ABC ,
则 = ,即 = ,解得t=4.8;
故所求t的值为3秒或4.8秒.
21.解:(1)当AD=CD时,如图,∠ACD=∠A=48°,
∵△BDC∽△BCA,
∴∠BCD=∠A=48°,
∴∠ACB=∠ACD+∠BCD=96°.
(2)由已知AC=AD=2,
∵△BCD∽△BAC,
∴=,
设BD=x,
∴()2=x(x+2),
∵x>0,
∴x=﹣1,
∵△BCD∽△BAC,
∴==
