人教版数学九年级上册24.1.4圆周角 课时练习 (含答案)
文档属性
| 名称 | 人教版数学九年级上册24.1.4圆周角 课时练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-31 00:00:00 | ||
图片预览




文档简介
2022-2023年人教版数学九年级上册24.1.4
《圆周角》课时练习
一 、选择题
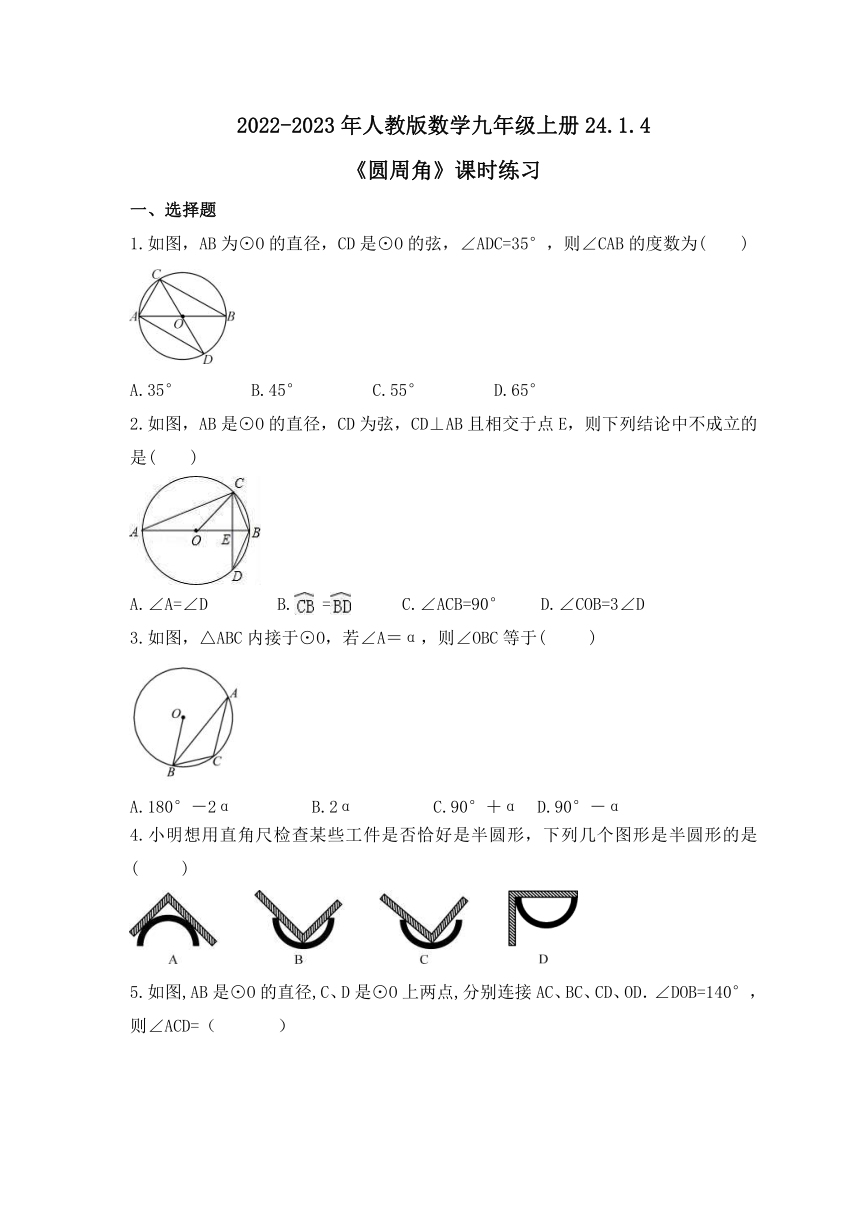
1.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )
A.∠A=∠D B. = C.∠ACB=90° D.∠COB=3∠D
3.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
4.小明想用直角尺检查某些工件是否恰好是半圆形,下列几个图形是半圆形的是( )
5.如图,AB是⊙O的直径,C、D是⊙O上两点,分别连接AC、BC、CD、OD.∠DOB=140°,则∠ACD=( )
A.20° B.30° C.40° D.70°
6.如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )
A.40° B.70° C.70°或80° D.80°或140°
7.若圆的一条弦把圆分成度数之比为1:3的两条弧,则这条弦所对的圆周角等于( )
A.45° B.135° C.90°和270 D.45°和135°
8.如图,已知☉O是△ABD的外接圆,AB是☉O直径,CD是☉O的弦,∠ABD=58°,
则∠BCD等于( )
A.16° B.32° C.58° D.64°
9.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,
则∠ACB=( )
A. 80° B. 90° C. 100° D. 无法确定
10.如图,已知⊙O是△ABD外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
A.116° B.64° C.58° D.32°
11.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
12.如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C.D.
二 、填空题
13.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,
则∠BCD的度数是 .
14.如图,已知四边形ABCD内接于⊙O,AD是直径,∠ABC=120°,CD=3,则弦AC= .
15.如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=______°.
16.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD= .
17.如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=,则AD=______.
18.在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值为 .
三 、解答题
19.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
20.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
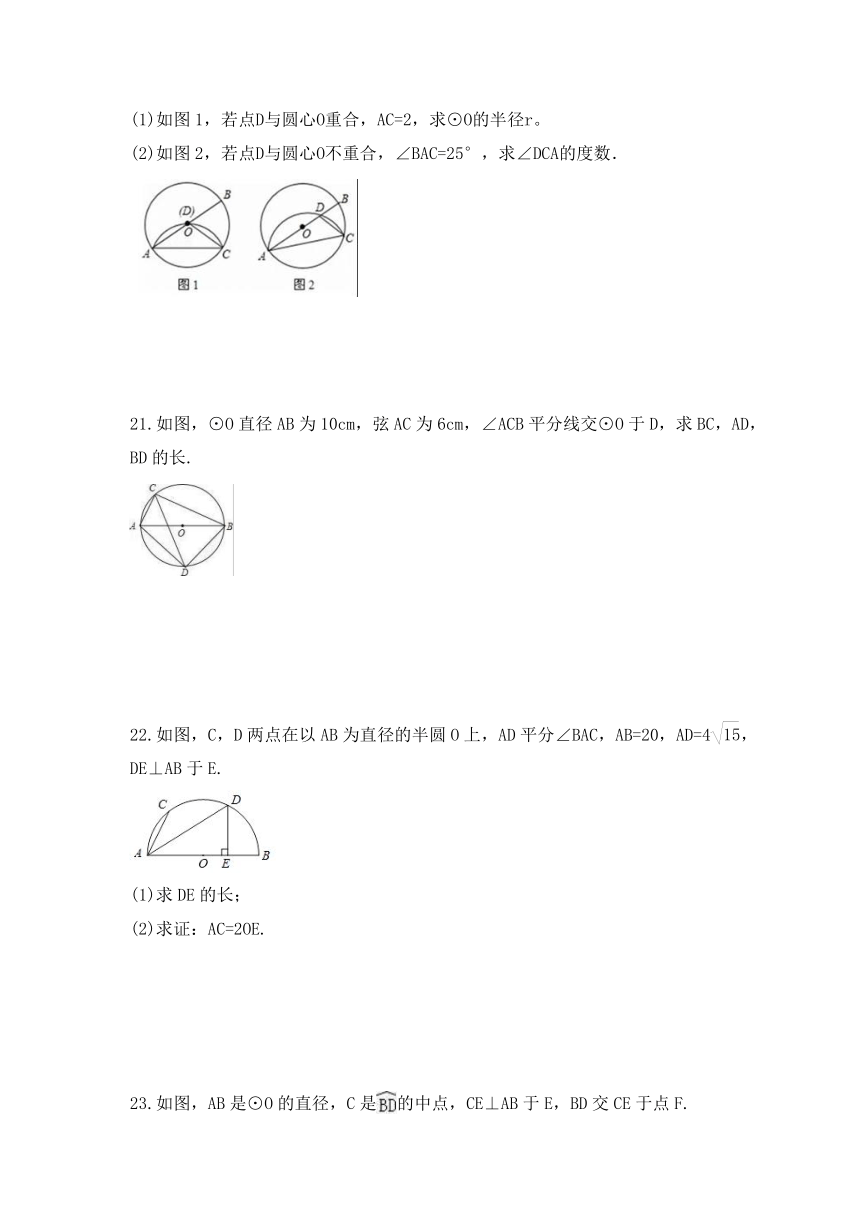
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r。
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
21.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
22.如图,C,D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4,DE⊥AB于E.
(1)求DE的长;
(2)求证:AC=2OE.
23.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
参考答案
1.C.
2.D.
3.D
4.B.
5.A;
6.D.
7.D
8.B
9.B
10.D
11.B.
12.B.
13.答案为:32°.
14.答案为:3.
15.答案为:48.
16.答案为:36°
17.答案为:4
18.答案为:4+2.
19.证明:(1)∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆= π 42=8π.
20.解:
21.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
22. (1)解:连接BD,∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,BD===4,
∵S△ADB=AD·BD=AB·DE,
∴AD·BD=AB·DE,
∴DE===4,即DE=4;
(2)证明:连接OD,作OF⊥AC于点F.
∵OF⊥AC,∴AC=2AF,
∵AD平分∠BAC,∴∠BAC=2∠BAD,
又∵∠BOD=2∠BAD,∴∠BAC=∠BOD,
Rt△OED和Rt△AFO中,
∵
∴△AFO≌△OED,
∴AF=OE,
∵AC=2AF,
∴AC=2OE.
23.(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是的中点,
∴=,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE=4.8,
故⊙O的半径为5,CE的长是4.8.
《圆周角》课时练习
一 、选择题
1.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
2.如图,AB是⊙O的直径,CD为弦,CD⊥AB且相交于点E,则下列结论中不成立的是( )
A.∠A=∠D B. = C.∠ACB=90° D.∠COB=3∠D
3.如图,△ABC内接于⊙O,若∠A=α,则∠OBC等于( )
A.180°-2α B.2α C.90°+α D.90°-α
4.小明想用直角尺检查某些工件是否恰好是半圆形,下列几个图形是半圆形的是( )
5.如图,AB是⊙O的直径,C、D是⊙O上两点,分别连接AC、BC、CD、OD.∠DOB=140°,则∠ACD=( )
A.20° B.30° C.40° D.70°
6.如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )
A.40° B.70° C.70°或80° D.80°或140°
7.若圆的一条弦把圆分成度数之比为1:3的两条弧,则这条弦所对的圆周角等于( )
A.45° B.135° C.90°和270 D.45°和135°
8.如图,已知☉O是△ABD的外接圆,AB是☉O直径,CD是☉O的弦,∠ABD=58°,
则∠BCD等于( )
A.16° B.32° C.58° D.64°
9.如图,经过原点O的⊙P与x、y轴分别交于A、B两点,点C是劣弧OB上一点,
则∠ACB=( )
A. 80° B. 90° C. 100° D. 无法确定
10.如图,已知⊙O是△ABD外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD等于( )
A.116° B.64° C.58° D.32°
11.如图,把直角三角板的直角顶点O放在破损玻璃镜的圆周上,两直角边与圆弧分别交于点M、N,量得OM=8cm,ON=6cm,则该圆玻璃镜的半径是( )
A. cm B.5cm C.6cm D.10cm
12.如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. B. C.D.
二 、填空题
13.如图,已知⊙O是△ABD的外接圆,AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,
则∠BCD的度数是 .
14.如图,已知四边形ABCD内接于⊙O,AD是直径,∠ABC=120°,CD=3,则弦AC= .
15.如图,AB是⊙O的直径,△ACD内接于⊙O,若∠BAC=42°,则∠ADC=______°.
16.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD= .
17.如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30°,BD是⊙O的直径,如果CD=,则AD=______.
18.在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值为 .
三 、解答题
19.如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
20.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r。
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
21.如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB平分线交⊙O于D,求BC,AD,BD的长.
22.如图,C,D两点在以AB为直径的半圆O上,AD平分∠BAC,AB=20,AD=4,DE⊥AB于E.
(1)求DE的长;
(2)求证:AC=2OE.
23.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD﹦6,AC﹦8,则⊙O的半径为______,CE的长是______.
参考答案
1.C.
2.D.
3.D
4.B.
5.A;
6.D.
7.D
8.B
9.B
10.D
11.B.
12.B.
13.答案为:32°.
14.答案为:3.
15.答案为:48.
16.答案为:36°
17.答案为:4
18.答案为:4+2.
19.证明:(1)∵AB是直径,
∴∠AEB=90°,
∴AE⊥BC,
∵AB=AC,
∴BE=CE,
∵AE=EF,
∴四边形ABFC是平行四边形,
∵AC=AB,
∴四边形ABFC是菱形.
(2)设CD=x.连接BD.
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴AB2﹣AD2=CB2﹣CD2,
∴(7+x)2﹣72=42﹣x2,解得x=1或﹣8(舍弃)
∴AC=8,BD==,
∴S菱形ABFC=8.
∴S半圆= π 42=8π.
20.解:
21.解:∵AB是直径
∴∠ACB=∠ADB=90°
在Rt△ABC中,AB2=AC2+BC2,AB=10cm,AC=6cm
∴BC2=AB2﹣AC2=102﹣62=64
∴BC==8(cm)
又CD平分∠ACB,
∴∠ACD=∠BCD,
∴
∴AD=BD
又在Rt△ABD中,AD2+BD2=AB2
∴AD2+BD2=102
∴AD=BD==5(cm).
22. (1)解:连接BD,∵AB为直径,
∴∠ADB=90°,
在Rt△ADB中,BD===4,
∵S△ADB=AD·BD=AB·DE,
∴AD·BD=AB·DE,
∴DE===4,即DE=4;
(2)证明:连接OD,作OF⊥AC于点F.
∵OF⊥AC,∴AC=2AF,
∵AD平分∠BAC,∴∠BAC=2∠BAD,
又∵∠BOD=2∠BAD,∴∠BAC=∠BOD,
Rt△OED和Rt△AFO中,
∵
∴△AFO≌△OED,
∴AF=OE,
∵AC=2AF,
∴AC=2OE.
23.(1)证明:
∵AB是⊙O的直径,
∴∠ACB﹦90°
又∵CE⊥AB,
∴∠CEB﹦90°
∴∠2﹦90°﹣∠ACE﹦∠A,
∵C是的中点,
∴=,
∴∠1﹦∠A(等弧所对的圆周角相等),
∴∠1﹦∠2,
∴CF﹦BF;
(2)解:∵C是的中点,CD﹦6,
∴BC=6,
∵∠ACB﹦90°,
∴AB2=AC2+BC2,
又∵BC=CD,
∴AB2=64+36=100,
∴AB=10,
∴CE=4.8,
故⊙O的半径为5,CE的长是4.8.
同课章节目录
