高一下期物理人教版(2019)必修第二册 6.1 习题课:圆周运动的传动问题和周期性问题 课件(共15张PPT)
文档属性
| 名称 | 高一下期物理人教版(2019)必修第二册 6.1 习题课:圆周运动的传动问题和周期性问题 课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 758.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 10:17:28 | ||
图片预览

文档简介
(共15张PPT)
第六章 圆周运动
6.1 习题课:圆周运动的传动问题和周期性问题
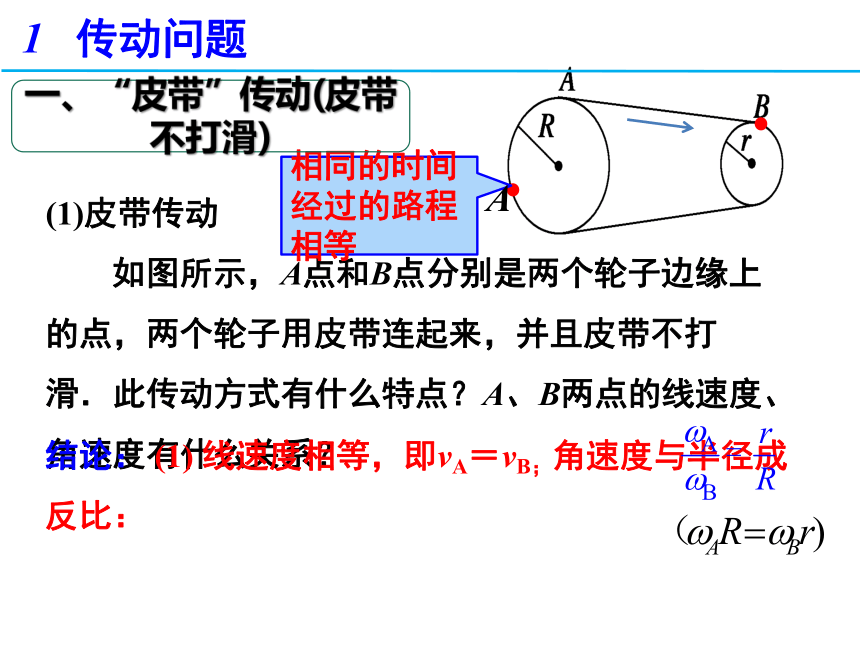
(1)皮带传动
如图所示,A点和B点分别是两个轮子边缘上的点,两个轮子用皮带连起来,并且皮带不打滑.此传动方式有什么特点?A、B两点的线速度、角速度有什么关系?
结论: (1) 线速度相等,即vA=vB;角速度与半径成反比:
相同的时间经过的路程相等
A
传动问题
1
一、“皮带”传动(皮带不打滑)
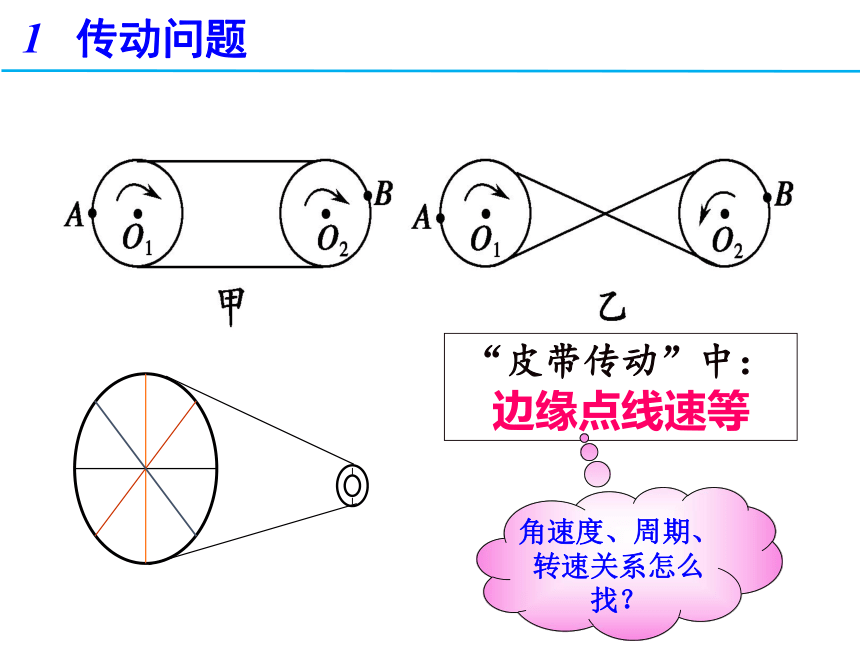
“皮带传动”中:
边缘点线速等
角速度、周期、转速关系怎么找?
传动问题
1
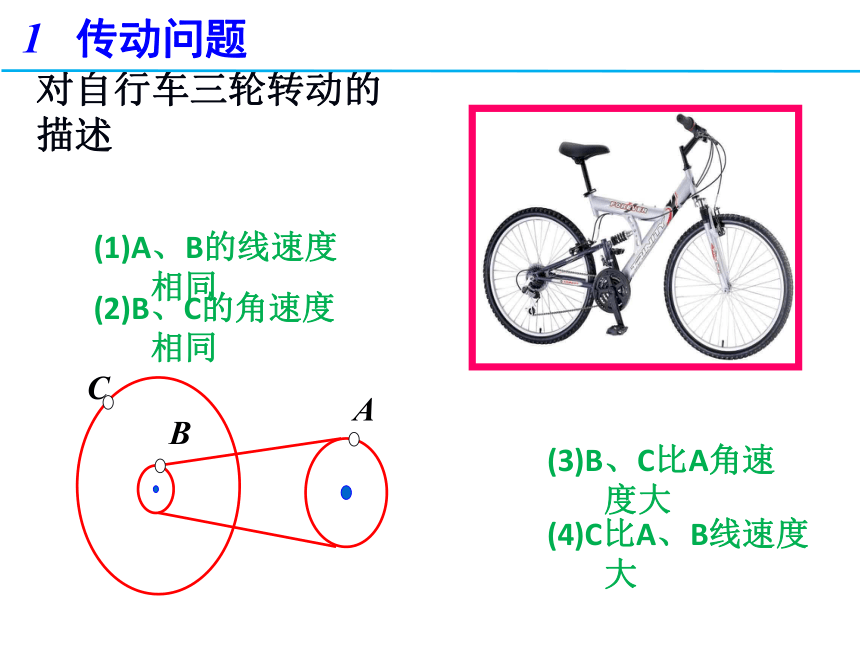
对自行车三轮转动的描述
(1)A、B的线速度相同
(2)B、C的角速度相同
(3)B、C比A角速度大
(4)C比A、B线速度大
C
B
A
传动问题
1
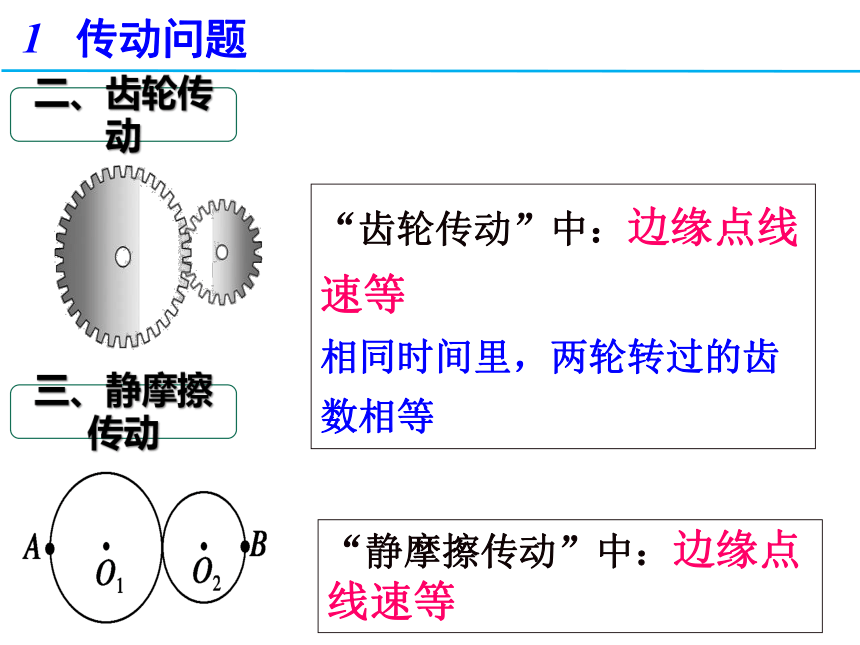
“齿轮传动”中:边缘点线速等
相同时间里,两轮转过的齿数相等
“静摩擦传动”中:边缘点线速等
二、齿轮传动
三、静摩擦传动
传动问题
1
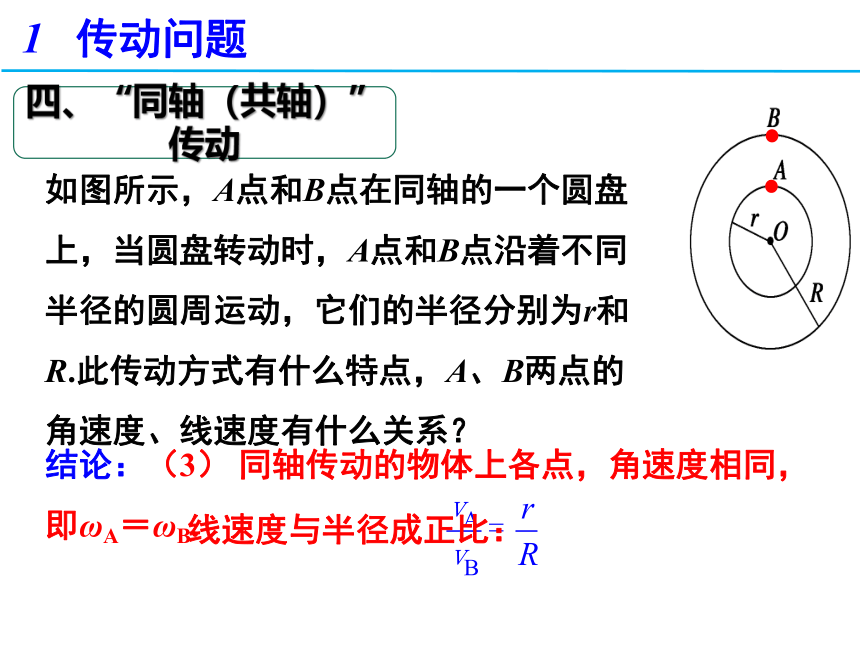
如图所示,A点和B点在同轴的一个圆盘上,当圆盘转动时,A点和B点沿着不同半径的圆周运动,它们的半径分别为r和R.此传动方式有什么特点,A、B两点的角速度、线速度有什么关系?
结论:(3) 同轴传动的物体上各点,角速度相同,即ωA=ωB.
线速度与半径成正比:
传动问题
1
四、“同轴(共轴)”传动
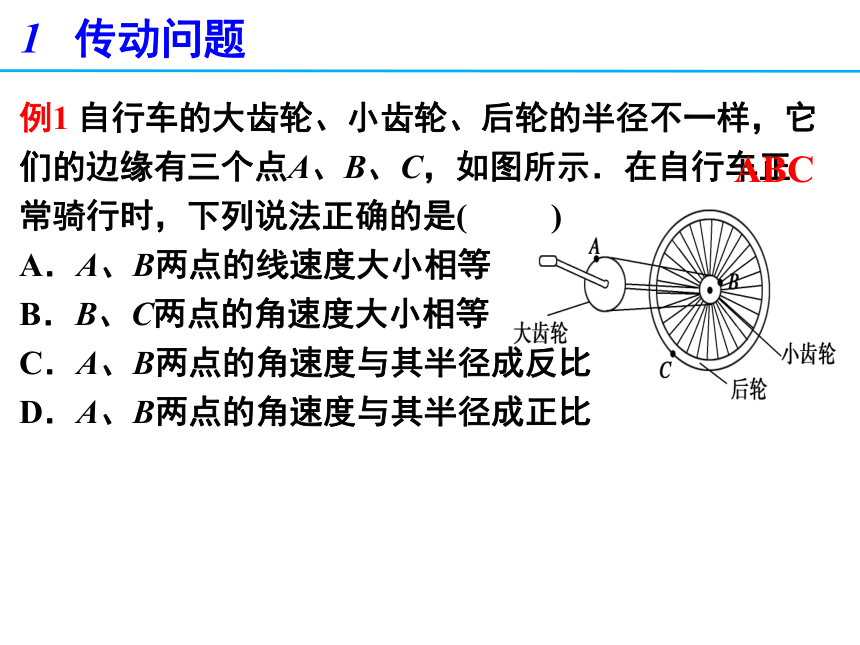
例1 自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,如图所示.在自行车正常骑行时,下列说法正确的是( )
A.A、B两点的线速度大小相等
B.B、C两点的角速度大小相等
C.A、B两点的角速度与其半径成反比
D.A、B两点的角速度与其半径成正比
ABC
传动问题
1
例2 如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2∶1 B.1∶2
C.1∶1 D.1∶4
B
传动问题
1
温馨提示:皮带传动、链条传动、摩擦传动、齿轮传动规律相同:轮缘线速度相等。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体.
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等).
(3)运动的关系:根据两物体运动的时间相等建立等式,求解待求物理量.
周期性和多解问题
2
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间相等.
(2)先特殊后一般:先考虑第一个周期的情况,再根据运动的周期性,考虑多个周期时的规律.
(3)分析时注意两个运动是独立的,互不影响.
周期性和多解问题
2
例1 如图所示,直径为d的纸筒以角速度ω绕轴O匀速转动,从枪口发射的子弹沿直径穿过圆筒.若子弹在圆筒旋转不到半周时在圆筒上留下a、b两个弹孔,已知aO和bO夹角为φ,则子弹的速度v大小是多少?
解析:如图,子弹应该从a孔射入b孔穿出,此过程中,圆筒转过的角度为π-φ,由角速度的公式有:
子弹速度为v,穿过两个孔所需时间:
由以上两式可解得:
周期性和多解问题
2
例2 如图3所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其正上方高h处沿OB方向水平抛出一小球,不计空气阻力,重力加速度为g,要使球与盘只碰一次,且落点为B,B为圆盘边缘上的点,求小球的初速度v的大小及圆盘转动的角速度ω.
周期性和多解问题
1
θ=n·2π(n=1,2,3…) 又因为θ=ωt
例3 如图4所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略重力、圆筒的阻力及空气阻力,则子弹的速度应满足什么条件?
周期性和多解问题
2
例4 半径R=1 m的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点,在O点的正上方将一个可视为质点的小球以4 m/s的速度水平抛出,半径OA方向恰好与该初速度的方向相同,如图所示,若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度大小可能是( )
A.4π rad/s B.6π rad/s
C.8π rad/s D.10π rad/s
C
周期性和多解问题
2
例5 为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min。子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示。则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
C
周期性和多解问题
2
第六章 圆周运动
6.1 习题课:圆周运动的传动问题和周期性问题
(1)皮带传动
如图所示,A点和B点分别是两个轮子边缘上的点,两个轮子用皮带连起来,并且皮带不打滑.此传动方式有什么特点?A、B两点的线速度、角速度有什么关系?
结论: (1) 线速度相等,即vA=vB;角速度与半径成反比:
相同的时间经过的路程相等
A
传动问题
1
一、“皮带”传动(皮带不打滑)
“皮带传动”中:
边缘点线速等
角速度、周期、转速关系怎么找?
传动问题
1
对自行车三轮转动的描述
(1)A、B的线速度相同
(2)B、C的角速度相同
(3)B、C比A角速度大
(4)C比A、B线速度大
C
B
A
传动问题
1
“齿轮传动”中:边缘点线速等
相同时间里,两轮转过的齿数相等
“静摩擦传动”中:边缘点线速等
二、齿轮传动
三、静摩擦传动
传动问题
1
如图所示,A点和B点在同轴的一个圆盘上,当圆盘转动时,A点和B点沿着不同半径的圆周运动,它们的半径分别为r和R.此传动方式有什么特点,A、B两点的角速度、线速度有什么关系?
结论:(3) 同轴传动的物体上各点,角速度相同,即ωA=ωB.
线速度与半径成正比:
传动问题
1
四、“同轴(共轴)”传动
例1 自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点A、B、C,如图所示.在自行车正常骑行时,下列说法正确的是( )
A.A、B两点的线速度大小相等
B.B、C两点的角速度大小相等
C.A、B两点的角速度与其半径成反比
D.A、B两点的角速度与其半径成正比
ABC
传动问题
1
例2 如图所示,A、B两轮属于摩擦传动,两轮半径RA=2RB,P、Q为两轮边缘上的点,当主动轮A匀速转动时,P、Q两点角速度大小之比为( )
A.2∶1 B.1∶2
C.1∶1 D.1∶4
B
传动问题
1
温馨提示:皮带传动、链条传动、摩擦传动、齿轮传动规律相同:轮缘线速度相等。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体.
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动、匀速直线运动等).
(3)运动的关系:根据两物体运动的时间相等建立等式,求解待求物理量.
周期性和多解问题
2
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两运动的联系点——时间相等.
(2)先特殊后一般:先考虑第一个周期的情况,再根据运动的周期性,考虑多个周期时的规律.
(3)分析时注意两个运动是独立的,互不影响.
周期性和多解问题
2
例1 如图所示,直径为d的纸筒以角速度ω绕轴O匀速转动,从枪口发射的子弹沿直径穿过圆筒.若子弹在圆筒旋转不到半周时在圆筒上留下a、b两个弹孔,已知aO和bO夹角为φ,则子弹的速度v大小是多少?
解析:如图,子弹应该从a孔射入b孔穿出,此过程中,圆筒转过的角度为π-φ,由角速度的公式有:
子弹速度为v,穿过两个孔所需时间:
由以上两式可解得:
周期性和多解问题
2
例2 如图3所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其正上方高h处沿OB方向水平抛出一小球,不计空气阻力,重力加速度为g,要使球与盘只碰一次,且落点为B,B为圆盘边缘上的点,求小球的初速度v的大小及圆盘转动的角速度ω.
周期性和多解问题
1
θ=n·2π(n=1,2,3…) 又因为θ=ωt
例3 如图4所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略重力、圆筒的阻力及空气阻力,则子弹的速度应满足什么条件?
周期性和多解问题
2
例4 半径R=1 m的水平圆盘绕过圆心O的竖直轴匀速转动,A为圆盘边缘上一点,在O点的正上方将一个可视为质点的小球以4 m/s的速度水平抛出,半径OA方向恰好与该初速度的方向相同,如图所示,若小球与圆盘只碰一次,且落在A点,则圆盘转动的角速度大小可能是( )
A.4π rad/s B.6π rad/s
C.8π rad/s D.10π rad/s
C
周期性和多解问题
2
例5 为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min。子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示。则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
C
周期性和多解问题
2
