苏科版 九年级下册 二次函数复习 课件(28张)
文档属性
| 名称 | 苏科版 九年级下册 二次函数复习 课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-31 11:27:03 | ||
图片预览






文档简介
二次函数单元复习
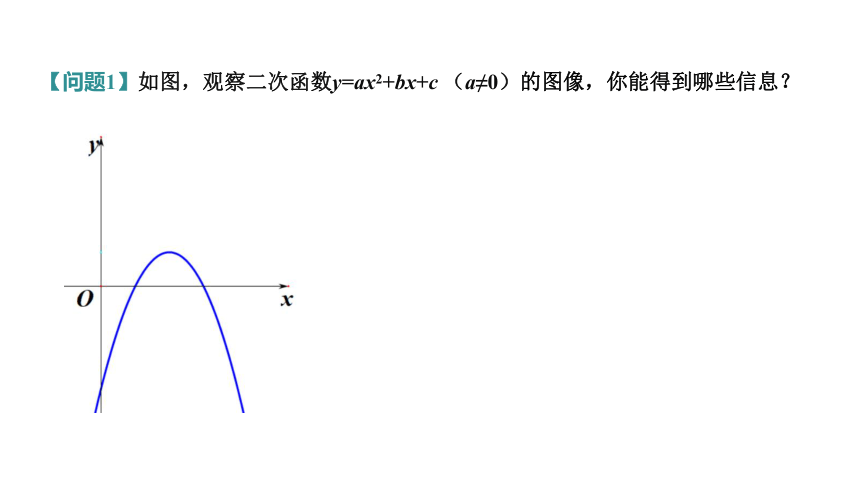
【问题1】如图,观察二次函数y=ax2+bx+c (a≠0)的图像,你能得到哪些信息?
字母的符号
图像的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图像过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
图像的位置与系数a、b、c的关系
【问题2】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0).
a、b、c有何相等或不等关系?你能比较a、c的大小吗?
【问题3】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),抛物线的对称轴是直线x = 2.
(1) 你还能得出哪些信息?
(2) 你能求出关于x的方程ax2+bx+c =0的解吗?
交点
图像
交点坐标
对称轴
方程文字描述
对应交点描述
韦达定理
韦定的运用
△=????2?4????????
?
2个
1个
0个
????1≠????2
?
????1=????2
?
无交点
????=????1+????22
?
两个不等实根
两个相等实根
无实根
两个不同交点
一个交点
没有交点
????1+????2=?????????
?
????1????2=????????
?
1????1+1????2=????1+????2????1????2=?????????????????=?????????
?
????1?????2=????1?????22=????1+????22?4????1????2
?
△ > 0
△= 0
△< 0
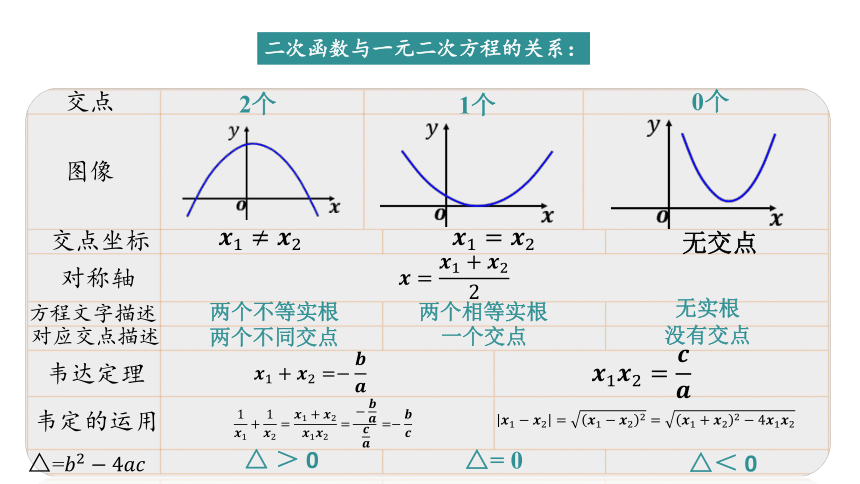
二次函数与一元二次方程的关系:
(3)若点C(-3, y1),D(-1, y2),E(4, y3),F(5, y4)是函数图像上的四个点,试比较y1、 y2、 y3、y4的大小关系.
(4)若x <a时,y随x的增大而增大,求 a的取值范围.
【问题3】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),抛物线的对称轴是直线x = 2.
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
开口方向
向上
向下
顶点坐标
对称轴
直线x=
直线x=
增减性
当x< 时,y随x的增大而减小;
当x> 时, y随x的增大而增大
当x< 时,y随x的增大而增大;当x> 时, y随x的增大而减小
最值
当x= 时,y有最小值,为
当x= 时,y有最大值,为
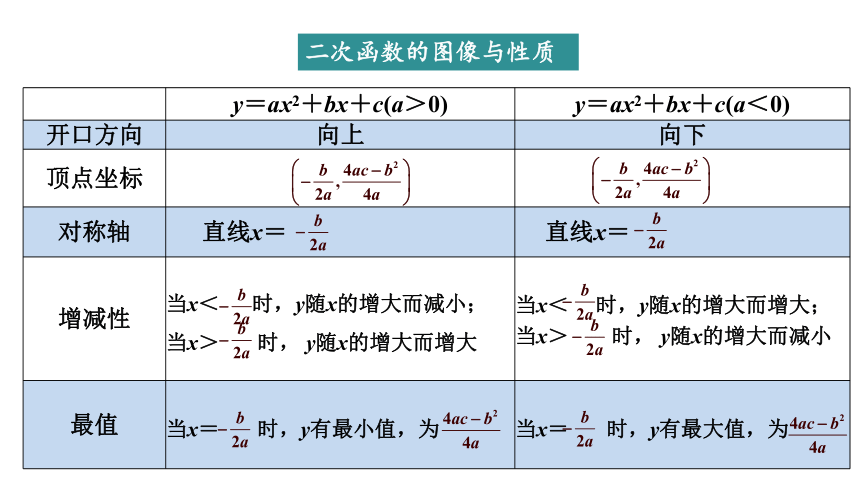
二次函数的图像与性质
【问题4】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3).
(1) 你能求出二次函数的表达式吗?
待定系数法求函数表达式
基本步骤:
函数表达式的选择:
【问题5】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3).
(1) 当0<x<1时,求y的取值范围.
(2) 当1<x<4时,求y的取值范围.
(3) 当y>0时,求x的取值范围.
(4) 当y<-3时,求x的取值范围.
二次函数与不等式
不等式的解集转化为二次函数自变量????的取值范围
?
根的判别式△
图像举例
与????轴交点
?
????????????+????????+????>????
的解集情况
?
????????????+????????+????<?????
的解集情况
?
△=????2?4????????>0
?
△=????2?4????????=0
?
△=????2?4????????<0
?
2个
1个
无
????????2
?
????≠?????2????
?
????取任意实数
?
????1?
无解
无解
二次函数与不等式的关系
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(1) 你能求出直线BC的表达式吗?
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3),直线l与抛物线交于点B、C.
(2)若点P为直线BC上一点,点P到A 、 B两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点P,求新抛物线的顶点坐标.
二次函数的平移
(3) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,求线段MN的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(4) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,过点N作NH⊥BC,求线段NH的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
化斜为直
(5) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,过点N作NH⊥BC,求△MNH周长的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(1) 抛物线是否存在点N使得△NBC面积与△ABC的面积相等?若存在,求出点N的坐标.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(2) 若点N是直线BC上方抛物线上一点,求△NBC面积的最大值.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(2) 若点N是直线BC上方抛物线上一点,求△NBC面积的最大值.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
若点N是直线BC上方抛物线上一点,是否存在点N使得△NBC是以BC为底的等腰三角形?若存在,求出点N的坐标.
二次函数中的等腰三角形存在性
【问题8】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的平行四边形存在性
过点C作x轴的平行线,交抛物线于点D,点 M在抛物线上,点 N在抛物线在对称轴上,是否存在以A、D、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标.
【问题9】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
y=ax2+bx+c (a≠0)
y=a(x + h)2+k (a≠0)
y=a(x-????????)(x-????????)(a≠0)
?
配方
因式分解
(????????,0) (????????,0)
?
(0,c )
(- h,k )
线段
角
三角形
四边形
. . .
最值
面积
存在性
. . .
函数表达式
点的坐标
图 形
问 题
由特殊到一般
数形结合
转化
同学们,再见!
【问题1】如图,观察二次函数y=ax2+bx+c (a≠0)的图像,你能得到哪些信息?
字母的符号
图像的特征
a
a>0
开口向上
a<0
开口向下
b
ab>0(a,b同号)
对称轴在y轴左侧
ab<0(a,b异号)
对称轴在y轴右侧
c
c=0
图像过原点
c>0
与y轴正半轴相交
c<0
与y轴负半轴相交
图像的位置与系数a、b、c的关系
【问题2】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0).
a、b、c有何相等或不等关系?你能比较a、c的大小吗?
【问题3】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),抛物线的对称轴是直线x = 2.
(1) 你还能得出哪些信息?
(2) 你能求出关于x的方程ax2+bx+c =0的解吗?
交点
图像
交点坐标
对称轴
方程文字描述
对应交点描述
韦达定理
韦定的运用
△=????2?4????????
?
2个
1个
0个
????1≠????2
?
????1=????2
?
无交点
????=????1+????22
?
两个不等实根
两个相等实根
无实根
两个不同交点
一个交点
没有交点
????1+????2=?????????
?
????1????2=????????
?
1????1+1????2=????1+????2????1????2=?????????????????=?????????
?
????1?????2=????1?????22=????1+????22?4????1????2
?
△ > 0
△= 0
△< 0
二次函数与一元二次方程的关系:
(3)若点C(-3, y1),D(-1, y2),E(4, y3),F(5, y4)是函数图像上的四个点,试比较y1、 y2、 y3、y4的大小关系.
(4)若x <a时,y随x的增大而增大,求 a的取值范围.
【问题3】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),抛物线的对称轴是直线x = 2.
y=ax2+bx+c(a>0)
y=ax2+bx+c(a<0)
开口方向
向上
向下
顶点坐标
对称轴
直线x=
直线x=
增减性
当x< 时,y随x的增大而减小;
当x> 时, y随x的增大而增大
当x< 时,y随x的增大而增大;当x> 时, y随x的增大而减小
最值
当x= 时,y有最小值,为
当x= 时,y有最大值,为
二次函数的图像与性质
【问题4】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3).
(1) 你能求出二次函数的表达式吗?
待定系数法求函数表达式
基本步骤:
函数表达式的选择:
【问题5】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3).
(1) 当0<x<1时,求y的取值范围.
(2) 当1<x<4时,求y的取值范围.
(3) 当y>0时,求x的取值范围.
(4) 当y<-3时,求x的取值范围.
二次函数与不等式
不等式的解集转化为二次函数自变量????的取值范围
?
根的判别式△
图像举例
与????轴交点
?
????????????+????????+????>????
的解集情况
?
????????????+????????+????<?????
的解集情况
?
△=????2?4????????>0
?
△=????2?4????????=0
?
△=????2?4????????<0
?
2个
1个
无
????????2
?
????≠?????2????
?
????取任意实数
?
????1?
无解
无解
二次函数与不等式的关系
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(1) 你能求出直线BC的表达式吗?
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴的交点是C(0,-3),直线l与抛物线交于点B、C.
(2)若点P为直线BC上一点,点P到A 、 B两点的距离相等,将该抛物线向左(或向右)平移,得到一条新抛物线,并且新抛物线经过点P,求新抛物线的顶点坐标.
二次函数的平移
(3) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,求线段MN的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(4) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,过点N作NH⊥BC,求线段NH的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
化斜为直
(5) 若点M是线段BC上的一点,过点M作x轴的垂线,交抛物线于点N,过点N作NH⊥BC,求△MNH周长的最大值.
二次函数中的最值
【问题6】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(1) 抛物线是否存在点N使得△NBC面积与△ABC的面积相等?若存在,求出点N的坐标.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(2) 若点N是直线BC上方抛物线上一点,求△NBC面积的最大值.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
(2) 若点N是直线BC上方抛物线上一点,求△NBC面积的最大值.
二次函数中的面积
【问题7】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
若点N是直线BC上方抛物线上一点,是否存在点N使得△NBC是以BC为底的等腰三角形?若存在,求出点N的坐标.
二次函数中的等腰三角形存在性
【问题8】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的平行四边形存在性
过点C作x轴的平行线,交抛物线于点D,点 M在抛物线上,点 N在抛物线在对称轴上,是否存在以A、D、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点M的坐标.
【问题9】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
二次函数中的等角存在性
M为抛物线上一点,是否存在∠ACM = ∠OCB ?若存在,求出点M的坐标.
【问题10】如图,若二次函数y=ax2+bx+c (a≠0)的图像与x轴的一个交点是A(1,0),
抛物线的对称轴是直线x = 2,抛物线与y轴交于点C(0,-3),直线l与抛物线交于点B、C.
y=ax2+bx+c (a≠0)
y=a(x + h)2+k (a≠0)
y=a(x-????????)(x-????????)(a≠0)
?
配方
因式分解
(????????,0) (????????,0)
?
(0,c )
(- h,k )
线段
角
三角形
四边形
. . .
最值
面积
存在性
. . .
函数表达式
点的坐标
图 形
问 题
由特殊到一般
数形结合
转化
同学们,再见!
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
