高一下期物理人教版(2019)必修第二册 8.3 动能和动能定理 第三课时(共22张PPT)
文档属性
| 名称 | 高一下期物理人教版(2019)必修第二册 8.3 动能和动能定理 第三课时(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 387.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 12:10:35 | ||
图片预览



文档简介
(共22张PPT)
第八章 机械能守恒定律
8.3 动能和动能定理
第三课时
分析多过程问题
1
动能定理与多过程问题相结合时,针对不同的运动过程可以分各个过程寻找做功与动能变化的关系,列动能定理方程。
在条件允许的情况下,或部分过程中条件不需要的情况下,可以针对全过程进行列式求解。
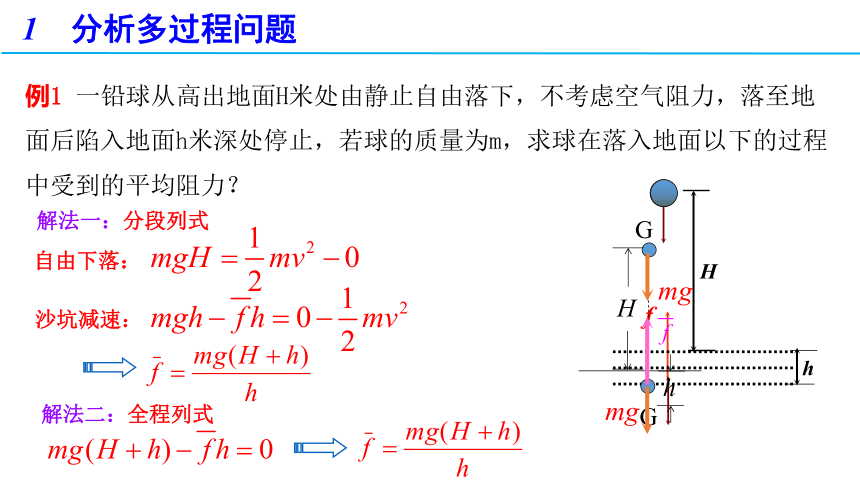
例1 一铅球从高出地面H米处由静止自由落下,不考虑空气阻力,落至地面后陷入地面h米深处停止,若球的质量为m,求球在落入地面以下的过程中受到的平均阻力?
分析多过程问题
1
f
G
G
H
h
解法一:分段列式
自由下落:
沙坑减速:
解法二:全程列式
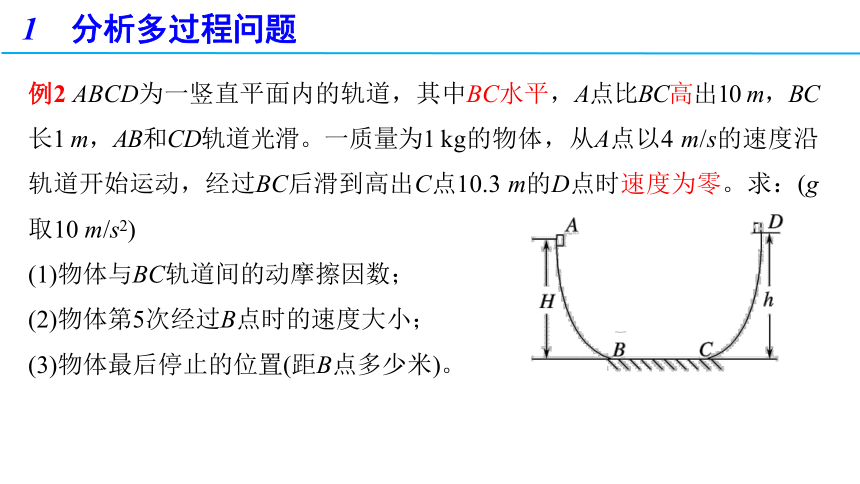
例2 ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出10 m,BC长1 m,AB和CD轨道光滑。一质量为1 kg的物体,从A点以4 m/s的速度沿轨道开始运动,经过BC后滑到高出C点10.3 m的D点时速度为零。求:(g取10 m/s2)
(1)物体与BC轨道间的动摩擦因数;
(2)物体第5次经过B点时的速度大小;
(3)物体最后停止的位置(距B点多少米)。
分析多过程问题
1
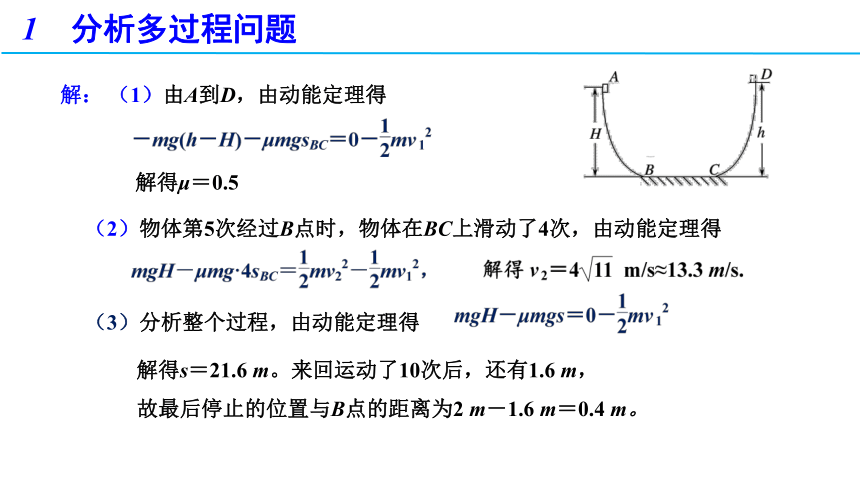
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
解: (1)由A到D,由动能定理得
解得μ=0.5
(3)分析整个过程,由动能定理得
解得s=21.6 m。来回运动了10次后,还有1.6 m,
故最后停止的位置与B点的距离为2 m-1.6 m=0.4 m。
分析多过程问题
1
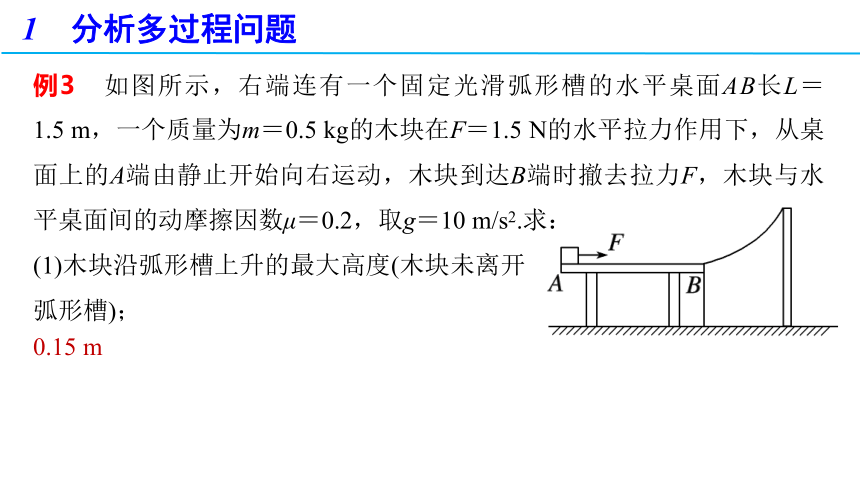
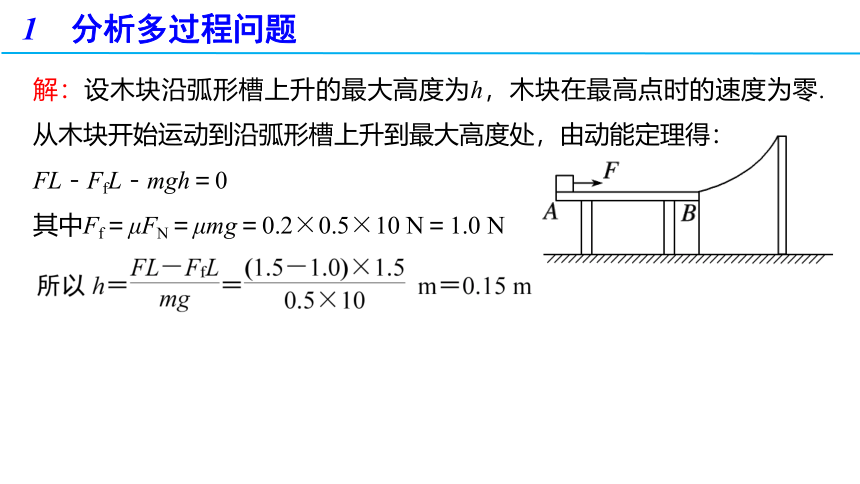
例3 如图所示,右端连有一个固定光滑弧形槽的水平桌面AB长L=
1.5 m,一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,取g=10 m/s2.求:
(1)木块沿弧形槽上升的最大高度(木块未离开弧形槽);
0.15 m
分析多过程问题
1
解:设木块沿弧形槽上升的最大高度为h,木块在最高点时的速度为零.从木块开始运动到沿弧形槽上升到最大高度处,由动能定理得:
FL-FfL-mgh=0
其中Ff=μFN=μmg=0.2×0.5×10 N=1.0 N
分析多过程问题
1
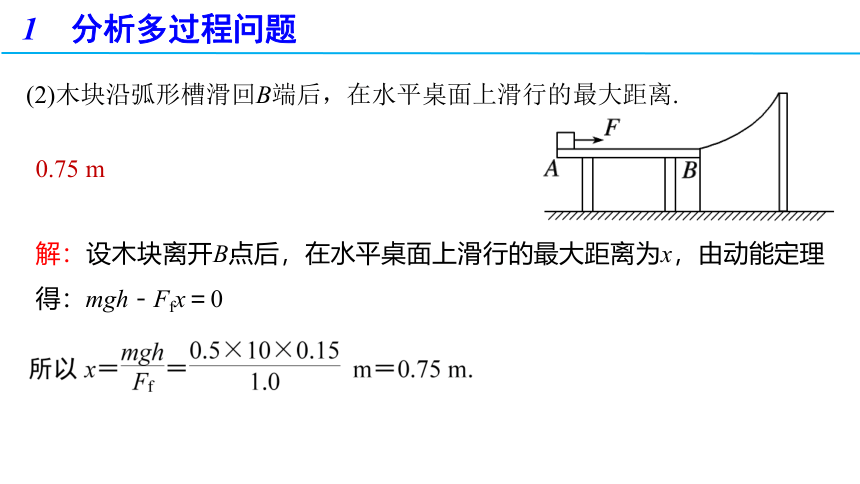
(2)木块沿弧形槽滑回B端后,在水平桌面上滑行的最大距离.
0.75 m
解:设木块离开B点后,在水平桌面上滑行的最大距离为x,由动能定理得:mgh-Ffx=0
分析多过程问题
1
例4 如图所示,质量m=0.1 kg的小球从距地面高H=5 m处自由下落,到达地面恰能沿凹陷于地面的半圆形槽壁的右端圆弧切入,半圆槽半径R=0.4 m.小球到达槽最低点时速率为
10 m/s,并继续沿槽壁运动直到从槽左端边缘竖直向上飞出……,如此反复,设小球在槽壁运动时受到的摩擦力大小恒定不变,不计空气阻力及小球与槽壁口接触时的能量损失,取g=10 m/s2.求:
(1)小球第一次离槽上升的高度H1;
4.2 m
分析多过程问题
1
解:由于对称性,在圆槽右半部分摩擦力对小球做的功与左半部分摩擦力对小球做的功相等.小球落至槽底部的整个过程中,由动能定理得mg(H+R)-Wf= mv2,
分析多过程问题
1
(2)小球最多能飞出槽外的次数.
6
解:设小球飞出槽外n次,则由动能定理得mgH-n·2Wf≥0
分析多过程问题
1
1.在有摩擦力做功的往复运动过程中,注意两种力做功的区别:
(1)重力做功只与初、末位置有关,而与路径无关;
(2)滑动摩擦力做功与路径有关,克服摩擦力做的功W克f=Ffs(s为路程).
2.由于动能定理解题的优越性,求多过程往复运动问题中的路程时,一般应用动能定理.
分析多过程问题
1
例5 如图所示,在北戴河旅游景点之一的南戴河滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),甲、乙两名旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处可认为是圆滑的,且无任何能量损失。则下列说法中正确的是( )
A.甲在B点的速率一定大于乙在B′点的速率
B.甲在B点的速率一定小于乙在B′点的速率
C.甲滑行的总路程一定等于乙滑行的总路程
D.甲、乙从A点出发到停下,两人位移的大小相等
分析多过程问题
1
√
√
动能定理常与平抛运动、圆周运动相结合,解决这类问题要特别注意:
(1)与平抛运动相结合时,要注意应用运动的合成与分解的方法,如分解位移或分解速度求平抛运动的有关物理量.
(2)与竖直平面内的圆周运动相结合时,应特别注意隐藏的临界条件:
①可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为vmin=0.
动能定理在平抛、圆周运动中的应用
2
例1 质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,如图所示,运动过程中小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点,此时绳子的张力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力所做的功为( )
A.mgR/4 B.mgR/3
C.mgR/2 D.mgR
O
m
动能定理在平抛、圆周运动中的应用
2
mg
F
f
V
重力做功:WG=-mg(2R)
拉力F不做功
空气阻力为变力,设其做功为W
小球从最低点到最高点中,由动能定理可得:
动能定理在平抛、圆周运动中的应用
2
解:小球从最低点到最高点中,由动能定理可得:
小球恰能通过最高点,由牛顿第二定律可得:
小球在最低点,由牛顿第二定律可得:
(1)
(3)
(2)
联立(1)(2)(3)式可得:
所以,小球克服空气阻力所做的功为:
动能定理在平抛、圆周运动中的应用
2
例2 如图所示,一长L=0.45 m、不可伸长的轻绳上端悬挂于M点,下端系一质量m=1.0 kg的小球,CDE是一竖直固定的圆弧形轨道,半径R=0.50 m,OC与竖直方向的夹角θ=60°,现将小球拉到A点(保持绳绷直且水平)由静止释放,当它经过B点时绳恰好被拉断,
小球平抛后,从圆弧形轨道的C点沿切线方向进入轨道,刚好能到达圆弧形轨道的最高点E,重力加速度g取10 m/s2,不计空气阻力,求:
(1)小球到B点时的速度大小;
3 m/s
动能定理在平抛、圆周运动中的应用
2
解析 小球从A到B的过程,由动能定理得
动能定理在平抛、圆周运动中的应用
2
(2)轻绳所受的最大拉力大小;
答案 30 N
动能定理在平抛、圆周运动中的应用
2
(3)小球在圆弧形轨道上运动时克服阻力做的功.
答案 8 J
动能定理在平抛、圆周运动中的应用
2
解析 小球从B到C做平抛运动,从C点沿切线进入圆弧形轨道,由平抛运动规律可得
动能定理在平抛、圆周运动中的应用
2
第八章 机械能守恒定律
8.3 动能和动能定理
第三课时
分析多过程问题
1
动能定理与多过程问题相结合时,针对不同的运动过程可以分各个过程寻找做功与动能变化的关系,列动能定理方程。
在条件允许的情况下,或部分过程中条件不需要的情况下,可以针对全过程进行列式求解。
例1 一铅球从高出地面H米处由静止自由落下,不考虑空气阻力,落至地面后陷入地面h米深处停止,若球的质量为m,求球在落入地面以下的过程中受到的平均阻力?
分析多过程问题
1
f
G
G
H
h
解法一:分段列式
自由下落:
沙坑减速:
解法二:全程列式
例2 ABCD为一竖直平面内的轨道,其中BC水平,A点比BC高出10 m,BC长1 m,AB和CD轨道光滑。一质量为1 kg的物体,从A点以4 m/s的速度沿轨道开始运动,经过BC后滑到高出C点10.3 m的D点时速度为零。求:(g取10 m/s2)
(1)物体与BC轨道间的动摩擦因数;
(2)物体第5次经过B点时的速度大小;
(3)物体最后停止的位置(距B点多少米)。
分析多过程问题
1
(2)物体第5次经过B点时,物体在BC上滑动了4次,由动能定理得
解: (1)由A到D,由动能定理得
解得μ=0.5
(3)分析整个过程,由动能定理得
解得s=21.6 m。来回运动了10次后,还有1.6 m,
故最后停止的位置与B点的距离为2 m-1.6 m=0.4 m。
分析多过程问题
1
例3 如图所示,右端连有一个固定光滑弧形槽的水平桌面AB长L=
1.5 m,一个质量为m=0.5 kg的木块在F=1.5 N的水平拉力作用下,从桌面上的A端由静止开始向右运动,木块到达B端时撤去拉力F,木块与水平桌面间的动摩擦因数μ=0.2,取g=10 m/s2.求:
(1)木块沿弧形槽上升的最大高度(木块未离开弧形槽);
0.15 m
分析多过程问题
1
解:设木块沿弧形槽上升的最大高度为h,木块在最高点时的速度为零.从木块开始运动到沿弧形槽上升到最大高度处,由动能定理得:
FL-FfL-mgh=0
其中Ff=μFN=μmg=0.2×0.5×10 N=1.0 N
分析多过程问题
1
(2)木块沿弧形槽滑回B端后,在水平桌面上滑行的最大距离.
0.75 m
解:设木块离开B点后,在水平桌面上滑行的最大距离为x,由动能定理得:mgh-Ffx=0
分析多过程问题
1
例4 如图所示,质量m=0.1 kg的小球从距地面高H=5 m处自由下落,到达地面恰能沿凹陷于地面的半圆形槽壁的右端圆弧切入,半圆槽半径R=0.4 m.小球到达槽最低点时速率为
10 m/s,并继续沿槽壁运动直到从槽左端边缘竖直向上飞出……,如此反复,设小球在槽壁运动时受到的摩擦力大小恒定不变,不计空气阻力及小球与槽壁口接触时的能量损失,取g=10 m/s2.求:
(1)小球第一次离槽上升的高度H1;
4.2 m
分析多过程问题
1
解:由于对称性,在圆槽右半部分摩擦力对小球做的功与左半部分摩擦力对小球做的功相等.小球落至槽底部的整个过程中,由动能定理得mg(H+R)-Wf= mv2,
分析多过程问题
1
(2)小球最多能飞出槽外的次数.
6
解:设小球飞出槽外n次,则由动能定理得mgH-n·2Wf≥0
分析多过程问题
1
1.在有摩擦力做功的往复运动过程中,注意两种力做功的区别:
(1)重力做功只与初、末位置有关,而与路径无关;
(2)滑动摩擦力做功与路径有关,克服摩擦力做的功W克f=Ffs(s为路程).
2.由于动能定理解题的优越性,求多过程往复运动问题中的路程时,一般应用动能定理.
分析多过程问题
1
例5 如图所示,在北戴河旅游景点之一的南戴河滑沙场有两个坡度不同的滑道AB和AB′(均可看作斜面),甲、乙两名旅游者分别乘两个完全相同的滑沙橇从A点由静止开始分别沿AB和AB′滑下,最后都停在水平沙面BC上。设滑沙橇和沙面间的动摩擦因数处处相同,斜面与水平面连接处可认为是圆滑的,且无任何能量损失。则下列说法中正确的是( )
A.甲在B点的速率一定大于乙在B′点的速率
B.甲在B点的速率一定小于乙在B′点的速率
C.甲滑行的总路程一定等于乙滑行的总路程
D.甲、乙从A点出发到停下,两人位移的大小相等
分析多过程问题
1
√
√
动能定理常与平抛运动、圆周运动相结合,解决这类问题要特别注意:
(1)与平抛运动相结合时,要注意应用运动的合成与分解的方法,如分解位移或分解速度求平抛运动的有关物理量.
(2)与竖直平面内的圆周运动相结合时,应特别注意隐藏的临界条件:
①可提供支撑效果的竖直平面内的圆周运动,物体能通过最高点的临界条件为vmin=0.
动能定理在平抛、圆周运动中的应用
2
例1 质量为m的小球被系在轻绳的一端,在竖直平面内做半径为R的圆周运动,如图所示,运动过程中小球受到空气阻力的作用,设某一时刻小球通过轨道的最低点,此时绳子的张力为7mg,此后小球继续做圆周运动,经过半个圆周恰能通过最高点,则在此过程中小球克服空气阻力所做的功为( )
A.mgR/4 B.mgR/3
C.mgR/2 D.mgR
O
m
动能定理在平抛、圆周运动中的应用
2
mg
F
f
V
重力做功:WG=-mg(2R)
拉力F不做功
空气阻力为变力,设其做功为W
小球从最低点到最高点中,由动能定理可得:
动能定理在平抛、圆周运动中的应用
2
解:小球从最低点到最高点中,由动能定理可得:
小球恰能通过最高点,由牛顿第二定律可得:
小球在最低点,由牛顿第二定律可得:
(1)
(3)
(2)
联立(1)(2)(3)式可得:
所以,小球克服空气阻力所做的功为:
动能定理在平抛、圆周运动中的应用
2
例2 如图所示,一长L=0.45 m、不可伸长的轻绳上端悬挂于M点,下端系一质量m=1.0 kg的小球,CDE是一竖直固定的圆弧形轨道,半径R=0.50 m,OC与竖直方向的夹角θ=60°,现将小球拉到A点(保持绳绷直且水平)由静止释放,当它经过B点时绳恰好被拉断,
小球平抛后,从圆弧形轨道的C点沿切线方向进入轨道,刚好能到达圆弧形轨道的最高点E,重力加速度g取10 m/s2,不计空气阻力,求:
(1)小球到B点时的速度大小;
3 m/s
动能定理在平抛、圆周运动中的应用
2
解析 小球从A到B的过程,由动能定理得
动能定理在平抛、圆周运动中的应用
2
(2)轻绳所受的最大拉力大小;
答案 30 N
动能定理在平抛、圆周运动中的应用
2
(3)小球在圆弧形轨道上运动时克服阻力做的功.
答案 8 J
动能定理在平抛、圆周运动中的应用
2
解析 小球从B到C做平抛运动,从C点沿切线进入圆弧形轨道,由平抛运动规律可得
动能定理在平抛、圆周运动中的应用
2
