高一下期物理人教版(2019)必修第二册 8.4 机械能守恒定律 第一课时(共20张PPT)
文档属性
| 名称 | 高一下期物理人教版(2019)必修第二册 8.4 机械能守恒定律 第一课时(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 12:11:54 | ||
图片预览




文档简介
(共20张PPT)
第八章 机械能守恒定律
8.4 机械能守恒定律
第一课时
化学能
情景引入 感知动能
0
风能
势能
动能
核能
既然能量对于人们的生产、生活如此重要,那究竟能量是什么呢?
由于能量过于抽象,要用一句话来来说明什么是能量并非易事,这也是牛顿未能把“能量”这一重要的概念留给我们的原因。
能量的概念是人类在对物质运动规律进行长期探索中逐渐建立起来的。但在牛顿之前的伽利略理想斜面实验中,我们就能发现它的萌芽。
追寻守恒量
1
A
B
h
h
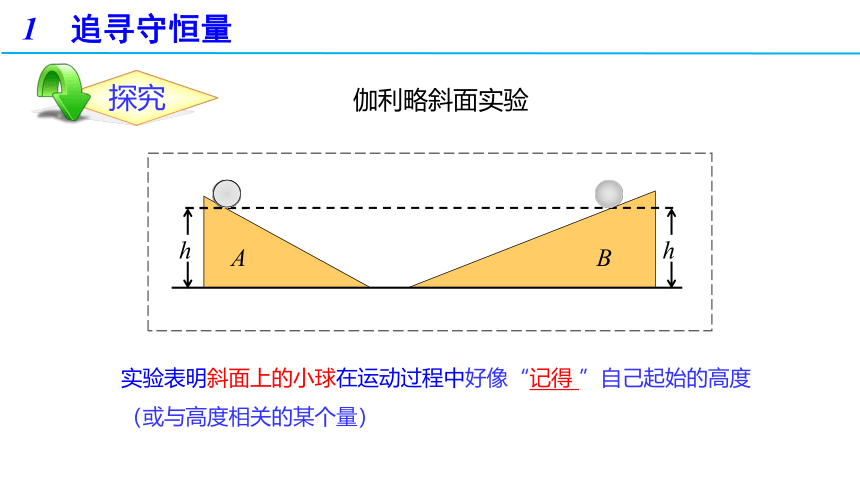
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)
伽利略斜面实验
探究
追寻守恒量
1
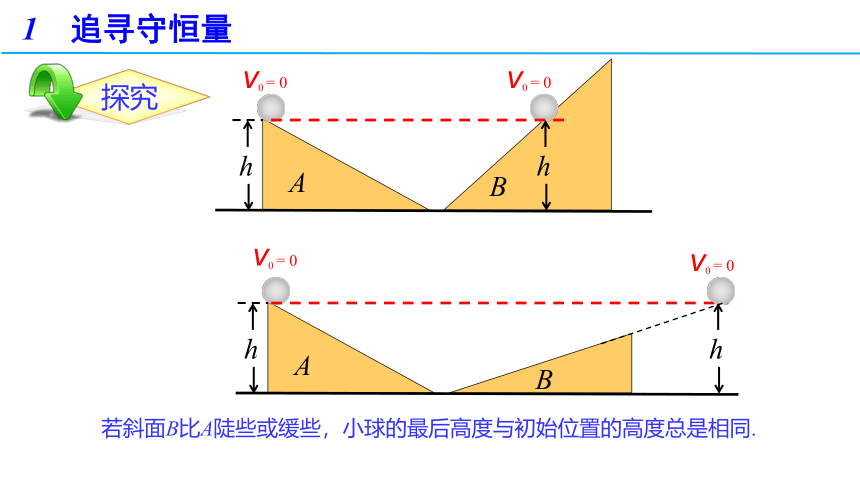
若斜面B比A陡些或缓些,小球的最后高度与初始位置的高度总是相同.
A
B
h
v0 = 0
A
B
h
v0 = 0
v0 = 0
v0 = 0
h
h
探究
追寻守恒量
1
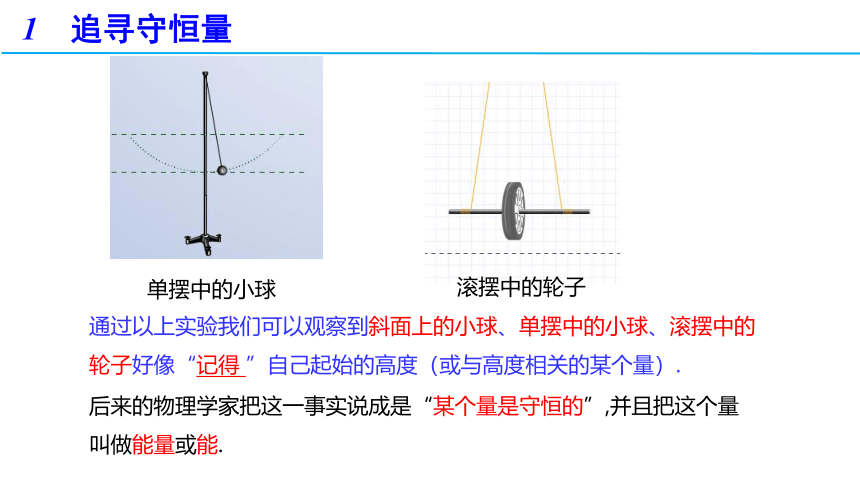
通过以上实验我们可以观察到斜面上的小球、单摆中的小球、滚摆中的轮子好像“记得 ”自己起始的高度(或与高度相关的某个量).
单摆中的小球
滚摆中的轮子
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能.
追寻守恒量
1
蹦极运动
分析运动员下落过程中,动能和势能之间怎样转化的?
动能和势能的相互转化
2
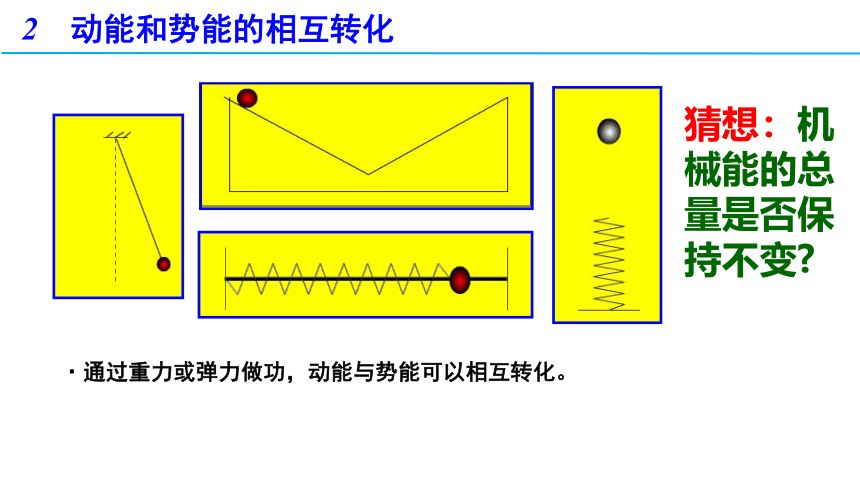
·通过重力或弹力做功,动能与势能可以相互转化。
猜想:机械能的总量是否保持不变
动能和势能的相互转化
2
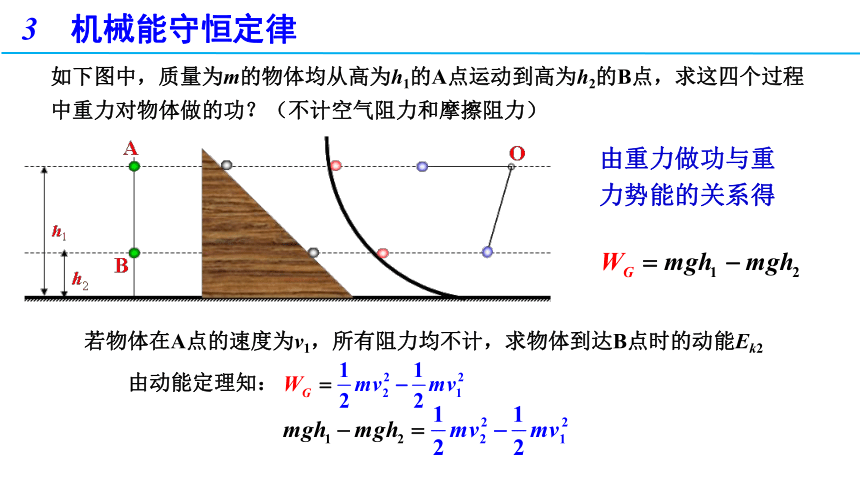
如下图中,质量为m的物体均从高为h1的A点运动到高为h2的B点,求这四个过程中重力对物体做的功?(不计空气阻力和摩擦阻力)
若物体在A点的速度为v1,所有阻力均不计,求物体到达B点时的动能Ek2
由动能定理知:
由重力做功与重力势能的关系得
机械能守恒定律
3
上述四例中有何共性?
故:
上式表示:动能和重力势能之和即总的机械能保持不变。
1.只有重力做功; 2.动能与势能在相互转化。
移项
即ΔEk= ΔEP
机械能守恒定律
3
v2
v1
物体沿光滑曲面滑下
h2
h1
选地面为参考平面
只在重力做功的物体系统内动能与重力势能可以相互转化而总的机械能保持不变
从A到B重力做功:
从A到B由动能定理得:
移项得:
机械能守恒定律
3
同样可以证明,只在弹力做功的物体系统内,动能与弹性势能可以相互转化,总的机械能也保持也不变.
O
B
C
机械能守恒定律
3
1. 定义:在只有重力做功或弹力做功的物体系统内,物体只发生动能与势能的相互转化,而总的机械能保持不变.
2. 机械能守恒条件
只有重力做功或弹力做功的物体系统内:
①不受其他力的作用;
②受其他力,但其他力不做功(或者其他力做功代数和为零).则该系统的机械能守恒.
机械能守恒定律
3
例1 判断下列各题中物体的机械能是否守恒?
将小球斜抛出后
木块沿光滑固定斜面下滑
降落伞匀速下降
G
G
G
FN
f
√
√
用绳拉着一个物体沿着光滑的斜面匀速上升。
×
×
典型例题分析
4
例2 把一个小球用细线悬挂起来,就成为一个摆,设实验中的小球的摆长为l,最大偏角为θ.忽略一切阻力,小球运动到最低位置时的速度是多大
典型例题分析
4
解:小球在摆动过程中,只有重力做功,机械能守恒.
选择小球在最低位置时所在的水平面为参考平面.
小球在最高点A时为初状态的机械能: Ek1+Ep1=mg(l-lcosθ)
小球在最低点O时为末状态的机械能为:Ek2+Ep2= mv2
根据机械能守恒定律有 : Ek2+Ep2=Ek1+Ep1
即 mv2= mgl ( 1- cosθ)
所以
用机械能守恒定律解决问题的基本思路
1.选取研究对象——物体系统.
2.根据研究对象所经历的物理过程.进行受力、做功分析,判断机械能是否守恒.
3.恰当地选取参考平面,确定研究对象在过程的初、末状态时的机械能.
4.根据机械能守恒定律列方程,进行求解并讨论解的准确性.
典型例题分析
4
3、机械能守恒定律:
2、机械能:E=Ek+Ep
(1)内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
(2)条件:只有重力、弹力做功
(3)结论: E1=E2
下降ΔEp减=ΔEk增
上升ΔEp增=ΔEk 减
1、伽利略斜面实验表明:“有某一量是守恒的”,这个量叫做能量。
小结
5
1.如图,一子弹以水平速度射入木块并留在其中,再与木块一起共同摆到最大高度的过程中,下列说法正确的是( )
A、子弹的机械能守恒
B、木块的机械能守恒
C、子弹和木块的总机械能守恒
D、以上说法都不对
D
子弹射中木块的过程机械能不守恒
整体从最低位置摆到最高位置的过程机械能守恒
课堂练习
6
2.如图所示,把一块质量是0.5kg的石头,从10m高处的山崖上以30°角,v0=5 m/s的速度朝斜上方抛出。(空气阻力不计) 求石头落地时速度的大小。
10m
只有重力做功,因此机械能守恒
由机械能守恒定律知:
所以,石头落地的速度为:
解:
课堂练习
6
由机械能守恒定律 Ek2 + Ep2 = Ek1 + Ep1 得
初态:
末态:
3. 长为 L 的均匀链条,放在光滑的水平桌面上,且使其长度的 垂在桌边,松手后链条从静止开始沿桌边下滑,则链条滑至刚刚离开桌边时的速度为多大?
课堂练习
6
第八章 机械能守恒定律
8.4 机械能守恒定律
第一课时
化学能
情景引入 感知动能
0
风能
势能
动能
核能
既然能量对于人们的生产、生活如此重要,那究竟能量是什么呢?
由于能量过于抽象,要用一句话来来说明什么是能量并非易事,这也是牛顿未能把“能量”这一重要的概念留给我们的原因。
能量的概念是人类在对物质运动规律进行长期探索中逐渐建立起来的。但在牛顿之前的伽利略理想斜面实验中,我们就能发现它的萌芽。
追寻守恒量
1
A
B
h
h
实验表明斜面上的小球在运动过程中好像“记得 ”自己起始的高度(或与高度相关的某个量)
伽利略斜面实验
探究
追寻守恒量
1
若斜面B比A陡些或缓些,小球的最后高度与初始位置的高度总是相同.
A
B
h
v0 = 0
A
B
h
v0 = 0
v0 = 0
v0 = 0
h
h
探究
追寻守恒量
1
通过以上实验我们可以观察到斜面上的小球、单摆中的小球、滚摆中的轮子好像“记得 ”自己起始的高度(或与高度相关的某个量).
单摆中的小球
滚摆中的轮子
后来的物理学家把这一事实说成是“某个量是守恒的”,并且把这个量叫做能量或能.
追寻守恒量
1
蹦极运动
分析运动员下落过程中,动能和势能之间怎样转化的?
动能和势能的相互转化
2
·通过重力或弹力做功,动能与势能可以相互转化。
猜想:机械能的总量是否保持不变
动能和势能的相互转化
2
如下图中,质量为m的物体均从高为h1的A点运动到高为h2的B点,求这四个过程中重力对物体做的功?(不计空气阻力和摩擦阻力)
若物体在A点的速度为v1,所有阻力均不计,求物体到达B点时的动能Ek2
由动能定理知:
由重力做功与重力势能的关系得
机械能守恒定律
3
上述四例中有何共性?
故:
上式表示:动能和重力势能之和即总的机械能保持不变。
1.只有重力做功; 2.动能与势能在相互转化。
移项
即ΔEk= ΔEP
机械能守恒定律
3
v2
v1
物体沿光滑曲面滑下
h2
h1
选地面为参考平面
只在重力做功的物体系统内动能与重力势能可以相互转化而总的机械能保持不变
从A到B重力做功:
从A到B由动能定理得:
移项得:
机械能守恒定律
3
同样可以证明,只在弹力做功的物体系统内,动能与弹性势能可以相互转化,总的机械能也保持也不变.
O
B
C
机械能守恒定律
3
1. 定义:在只有重力做功或弹力做功的物体系统内,物体只发生动能与势能的相互转化,而总的机械能保持不变.
2. 机械能守恒条件
只有重力做功或弹力做功的物体系统内:
①不受其他力的作用;
②受其他力,但其他力不做功(或者其他力做功代数和为零).则该系统的机械能守恒.
机械能守恒定律
3
例1 判断下列各题中物体的机械能是否守恒?
将小球斜抛出后
木块沿光滑固定斜面下滑
降落伞匀速下降
G
G
G
FN
f
√
√
用绳拉着一个物体沿着光滑的斜面匀速上升。
×
×
典型例题分析
4
例2 把一个小球用细线悬挂起来,就成为一个摆,设实验中的小球的摆长为l,最大偏角为θ.忽略一切阻力,小球运动到最低位置时的速度是多大
典型例题分析
4
解:小球在摆动过程中,只有重力做功,机械能守恒.
选择小球在最低位置时所在的水平面为参考平面.
小球在最高点A时为初状态的机械能: Ek1+Ep1=mg(l-lcosθ)
小球在最低点O时为末状态的机械能为:Ek2+Ep2= mv2
根据机械能守恒定律有 : Ek2+Ep2=Ek1+Ep1
即 mv2= mgl ( 1- cosθ)
所以
用机械能守恒定律解决问题的基本思路
1.选取研究对象——物体系统.
2.根据研究对象所经历的物理过程.进行受力、做功分析,判断机械能是否守恒.
3.恰当地选取参考平面,确定研究对象在过程的初、末状态时的机械能.
4.根据机械能守恒定律列方程,进行求解并讨论解的准确性.
典型例题分析
4
3、机械能守恒定律:
2、机械能:E=Ek+Ep
(1)内容:在只有重力或弹力做功的物体系统内,物体的动能和势能可以相互转化,而总的机械能保持不变。
(2)条件:只有重力、弹力做功
(3)结论: E1=E2
下降ΔEp减=ΔEk增
上升ΔEp增=ΔEk 减
1、伽利略斜面实验表明:“有某一量是守恒的”,这个量叫做能量。
小结
5
1.如图,一子弹以水平速度射入木块并留在其中,再与木块一起共同摆到最大高度的过程中,下列说法正确的是( )
A、子弹的机械能守恒
B、木块的机械能守恒
C、子弹和木块的总机械能守恒
D、以上说法都不对
D
子弹射中木块的过程机械能不守恒
整体从最低位置摆到最高位置的过程机械能守恒
课堂练习
6
2.如图所示,把一块质量是0.5kg的石头,从10m高处的山崖上以30°角,v0=5 m/s的速度朝斜上方抛出。(空气阻力不计) 求石头落地时速度的大小。
10m
只有重力做功,因此机械能守恒
由机械能守恒定律知:
所以,石头落地的速度为:
解:
课堂练习
6
由机械能守恒定律 Ek2 + Ep2 = Ek1 + Ep1 得
初态:
末态:
3. 长为 L 的均匀链条,放在光滑的水平桌面上,且使其长度的 垂在桌边,松手后链条从静止开始沿桌边下滑,则链条滑至刚刚离开桌边时的速度为多大?
课堂练习
6
