27.2.2 相似三角形应用举例(第二课时)
文档属性
| 名称 | 27.2.2 相似三角形应用举例(第二课时) |  | |
| 格式 | zip | ||
| 文件大小 | 350.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-12 08:59:08 | ||
图片预览


文档简介
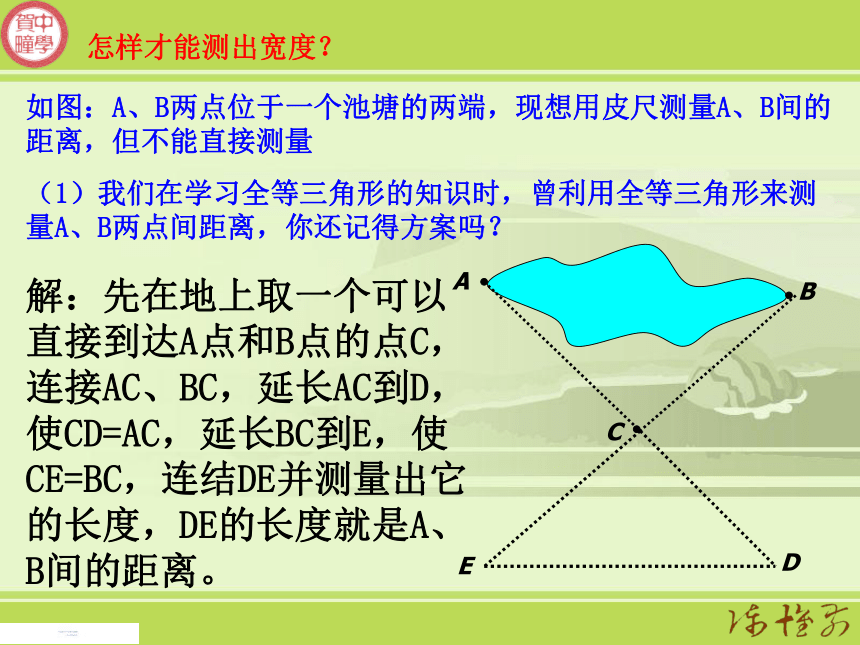
课件14张PPT。27.2.1 相似三角形应用举例(第二课时)如图:A、B两点位于一个池塘的两端,现想用皮尺测量A、B间的距离,但不能直接测量
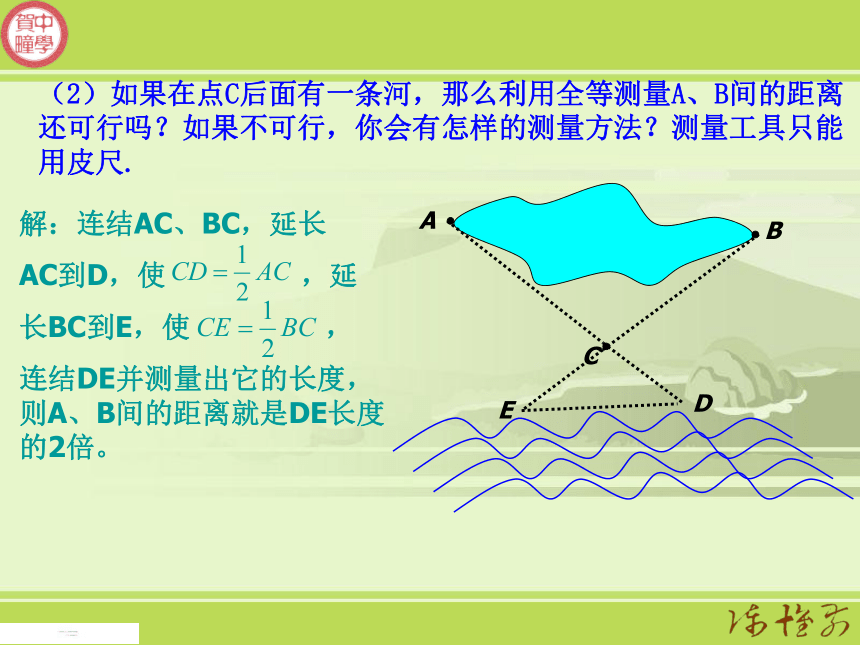
(1)我们在学习全等三角形的知识时,曾利用全等三角形来测量A、B两点间距离,你还记得方案吗?解:先在地上取一个可以直接到达A点和B点的点C,连接AC、BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连结DE并测量出它的长度,DE的长度就是A、B间的距离。怎样才能测出宽度?(2)如果在点C后面有一条河,那么利用全等测量A、B间的距离还可行吗?如果不可行,你会有怎样的测量方法?测量工具只能用皮尺.解:连结AC、BC,延长
AC到D,使 ,延
长BC到E,使 ,
连结DE并测量出它的长度,则A、B间的距离就是DE长度的2倍。
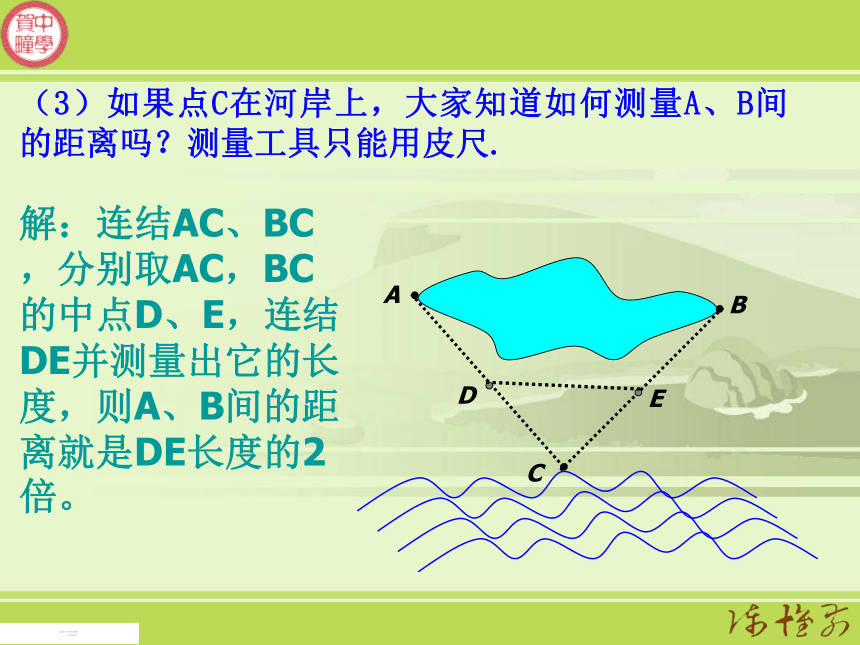
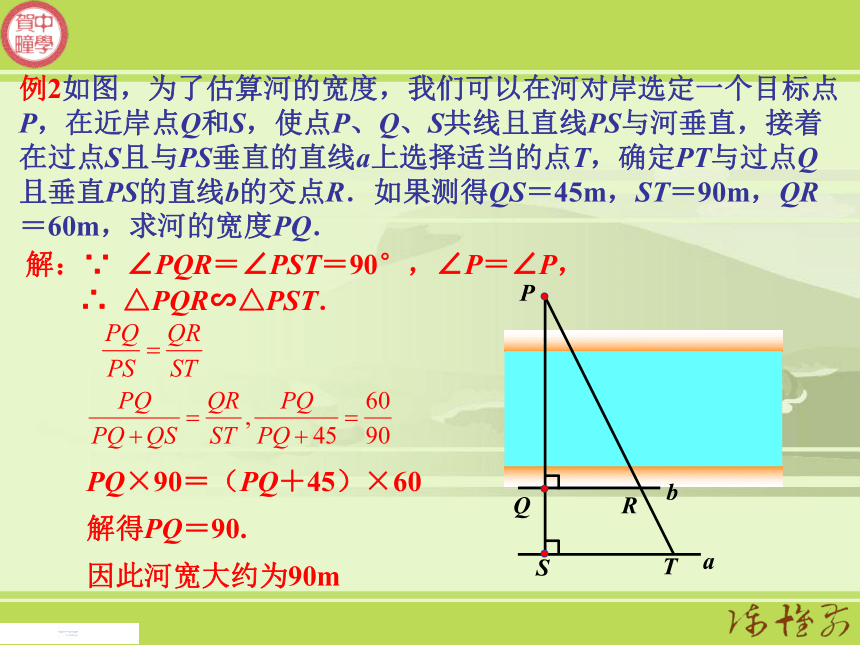
(3)如果点C在河岸上,大家知道如何测量A、B间的距离吗?测量工具只能用皮尺. 解:连结AC、BC,分别取AC,BC的中点D、E,连结DE并测量出它的长度,则A、B间的距离就是DE长度的2倍。例2如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.解:∵ ∠PQR=∠PST=90°,∠P=∠P,PQ×90=(PQ+45)×60解得PQ=90.PQRSTab∴ △PQR∽△PST.因此河宽大约为90m1.大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在对岸选定一个目标作为点A,再在运河的这一边选点B、C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点为D。(1)要估算运河的宽度,你认为要测量哪些可以测量的线段?(2)如果测得BD=120m,DC=60m,EC=50m,求出大运河的大致宽度AB。解:∵∠ADB=∠EDC, ∠ABC=∠ECD=90°
∴ΔABD∽ΔECD
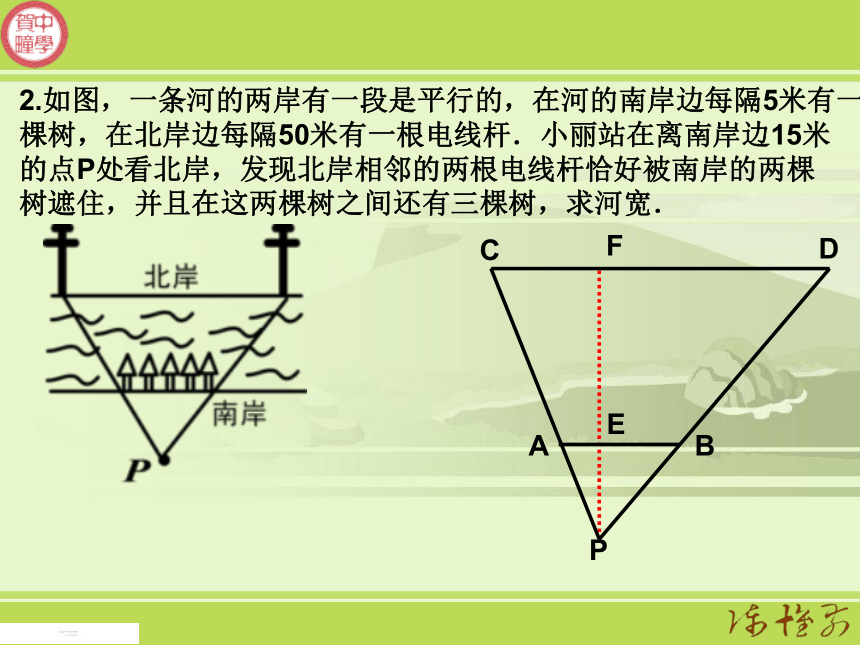
∴2.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一
棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米
的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵
树遮住,并且在这两棵树之间还有三棵树,求河宽.EF例3:已知左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。一个身高1.6m的人沿着正对着两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看见右边较高的树的顶端点C?
KⅡ盲区观察者看不到的区 域。仰角:视线在水平 线以上的夹角。水平线视线视点观察者眼睛的位置。(1)FBCDHGlAK(1)FBCDHGlAⅠK分析:假设观察者从左向右走到点E时,他的眼睛的位置点F与两颗树的顶端点A、C恰在一条直线上,如果观察者继续前进,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它。E由题意可知,AB⊥L,CD⊥L,
∴AB∥CD,△AFH∽ △CFK=解得FH=8∴当他与左边的树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,就不能看见右边较高的树的顶端点C亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.你能根据以上测量数据帮助他们求出住宅楼的高度吗?如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,
他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B
在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,
测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.如图,△ABC是一块锐角三角形余料,BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以利用相似三角形的知识解决
实际问题的步骤:1.建立数学模型2.求解得数学答案3.还原实际问题注意:先证明,后求解.
(1)我们在学习全等三角形的知识时,曾利用全等三角形来测量A、B两点间距离,你还记得方案吗?解:先在地上取一个可以直接到达A点和B点的点C,连接AC、BC,延长AC到D,使CD=AC,延长BC到E,使CE=BC,连结DE并测量出它的长度,DE的长度就是A、B间的距离。怎样才能测出宽度?(2)如果在点C后面有一条河,那么利用全等测量A、B间的距离还可行吗?如果不可行,你会有怎样的测量方法?测量工具只能用皮尺.解:连结AC、BC,延长
AC到D,使 ,延
长BC到E,使 ,
连结DE并测量出它的长度,则A、B间的距离就是DE长度的2倍。
(3)如果点C在河岸上,大家知道如何测量A、B间的距离吗?测量工具只能用皮尺. 解:连结AC、BC,分别取AC,BC的中点D、E,连结DE并测量出它的长度,则A、B间的距离就是DE长度的2倍。例2如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在近岸点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.解:∵ ∠PQR=∠PST=90°,∠P=∠P,PQ×90=(PQ+45)×60解得PQ=90.PQRSTab∴ △PQR∽△PST.因此河宽大约为90m1.大运河的两岸有一段是平行的,为了估算其运河的宽度,我们可以在对岸选定一个目标作为点A,再在运河的这一边选点B、C,使AB⊥BC,然后再选点E,使EC⊥BC,用视线确定BC和AE的交点为D。(1)要估算运河的宽度,你认为要测量哪些可以测量的线段?(2)如果测得BD=120m,DC=60m,EC=50m,求出大运河的大致宽度AB。解:∵∠ADB=∠EDC, ∠ABC=∠ECD=90°
∴ΔABD∽ΔECD
∴2.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一
棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米
的点P处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵
树遮住,并且在这两棵树之间还有三棵树,求河宽.EF例3:已知左,右并排的两棵大树的高分别是AB=8m和CD=12m,两树的根部的距离BD=5m。一个身高1.6m的人沿着正对着两棵树的一条水平直路从左向右前进,当他与左边较低的树的距离小于多少时,就不能看见右边较高的树的顶端点C?
KⅡ盲区观察者看不到的区 域。仰角:视线在水平 线以上的夹角。水平线视线视点观察者眼睛的位置。(1)FBCDHGlAK(1)FBCDHGlAⅠK分析:假设观察者从左向右走到点E时,他的眼睛的位置点F与两颗树的顶端点A、C恰在一条直线上,如果观察者继续前进,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,观察者看不到它。E由题意可知,AB⊥L,CD⊥L,
∴AB∥CD,△AFH∽ △CFK=解得FH=8∴当他与左边的树的距离小于8m时,由于这棵树的遮挡,右边树的顶端点C在观察者的盲区之内,就不能看见右边较高的树的顶端点C亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部M,颖颖的头顶B及亮亮的眼睛A恰在一条直线上时,两人分别标定自己的位置C,D.然后测出两人之间的距CD=1.25m,颖颖与楼之间的距离DN=30m(C,D,N在一条直线上),颖颖的身高BD=1.6m,亮亮蹲地观测时眼睛到地面的距离AC=0.8m.你能根据以上测量数据帮助他们求出住宅楼的高度吗?如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,
他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B
在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,
测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.如图,△ABC是一块锐角三角形余料,BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以利用相似三角形的知识解决
实际问题的步骤:1.建立数学模型2.求解得数学答案3.还原实际问题注意:先证明,后求解.
