14.2.1平方差公式
图片预览





文档简介
课件29张PPT。
14.2.1 平方差公式数学组:李红娟 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn.多项式与多项式相乘的法则 (x+1)(x-1) (2) (a+2)(a-2);
(3) (2x+1)(2x-1); (4) (3x+4y)(3x-4y). 观察上述算式,你能发现什么共同点?运算出结果后,你发现什么规律?计算: 阅读课本107页,回答以下问题:(时间3分钟)
1、你能从代数和几何两个角度证明公式吗?
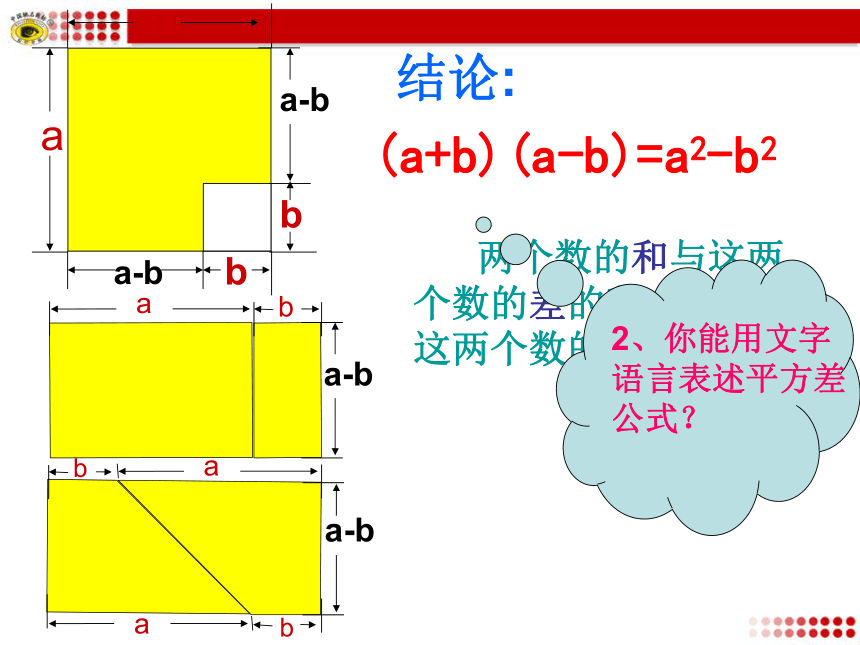
2、你用能文字语言表述平方差公式?
3、平方差公式有哪些特征呢?
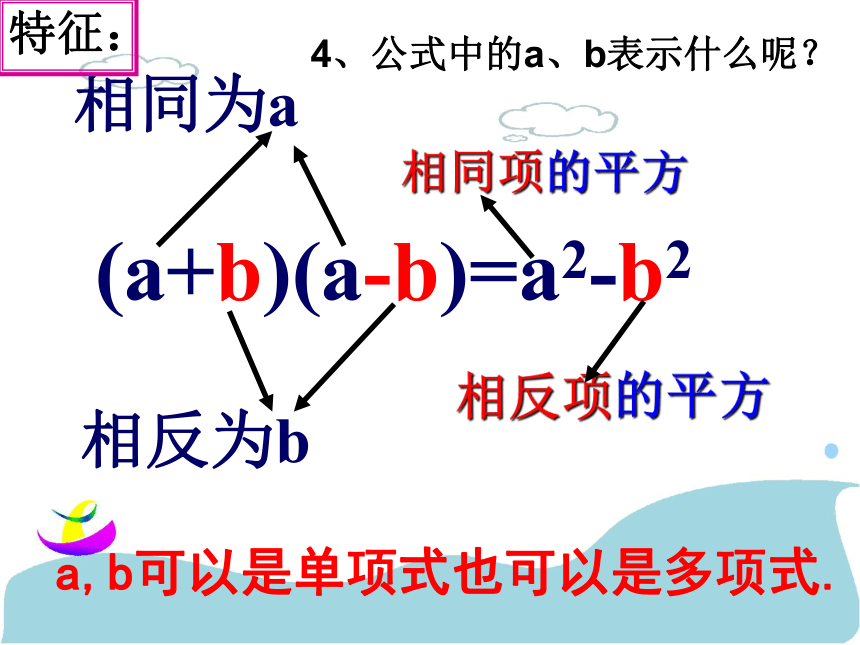
4、公式中的a、b表示什么呢?
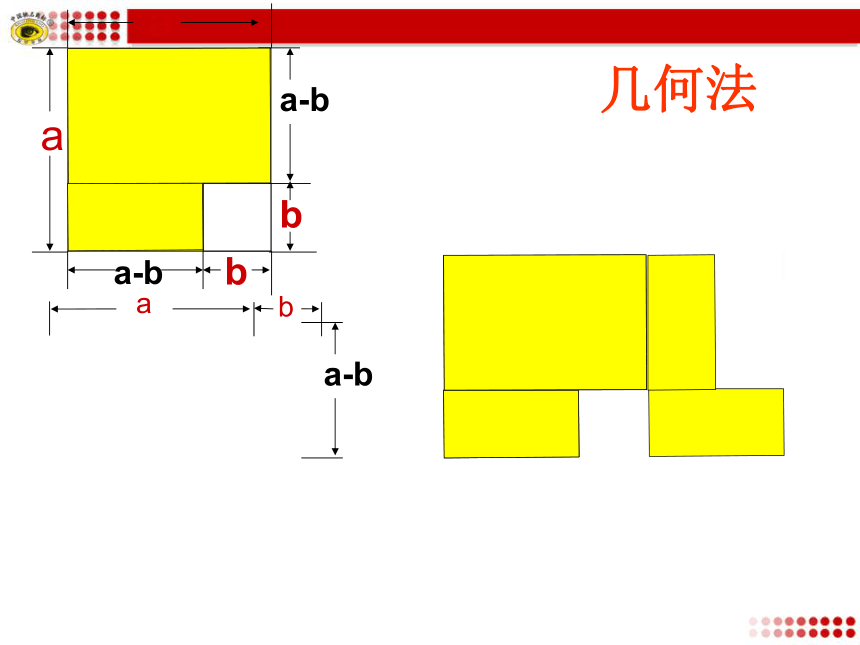
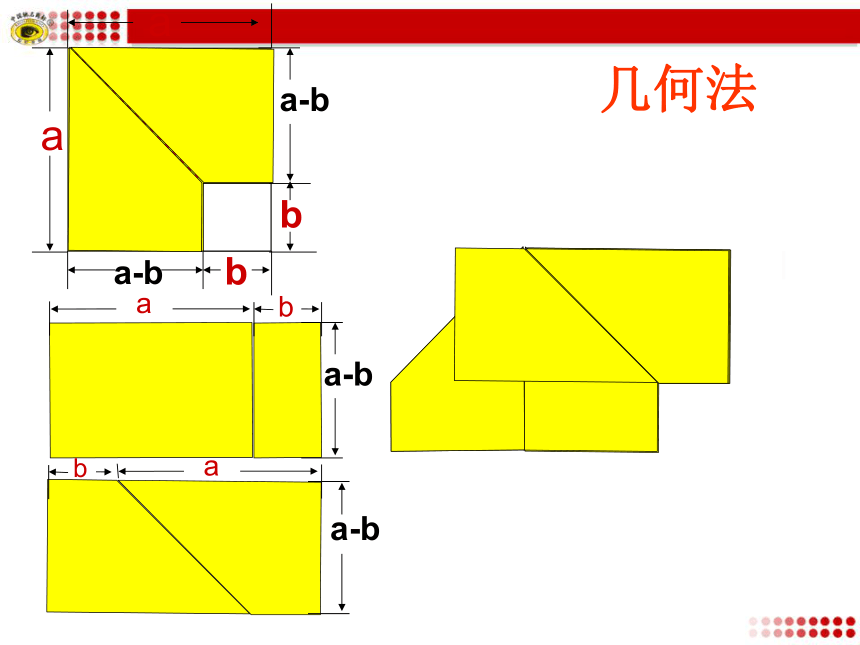
自学提纲代数法:ab几何法几何法(a+b)(a-b)=a2-b2结论: 两个数的和与这两个数的差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2相反为b 相同为a 特征:a,b可以是单项式也可以是多项式.4、公式中的a、b表示什么呢?第一关: ⑴ (3x+2)(3x-2) ;⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y);(4) (3m-4n)(-3m-4n);运用平方差公式计算:(5)(6-mn)(mn+6).第二关:下面各式的计算对不对?如果不对,应怎样改正?第三关:计算:第四关:计算:谈谈你的收获:(1)平方差公式是什么?它的文字语言如何叙述?
(2)平方差公式的特征是什么?
(3)应用平方差公式时要注意什么?
(4)本节课使用了哪些数学思想?作业:课本112页第一题1. (1+x)( 1-x)=1- 2. (-3+a)(-3- )= -a24. (0.3x-2)( )=4-0.09 x23. (x+a)(a )=a2 –x25. (ab )( -x)= x2 - 填空:使等式两边满足平方差公式x2a9-x-aba2b2-x第二关: 请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?(a+b)(a-b)=a2-b2图1图2【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) .(2) (b+2a)(2a-b). 【解析】 (1) (3x+2)(3x-2)=(3x)2-22=9x2-4.(2)(b+2a)(2a-b)=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.只有符合(a+b) (a- b)的
形式才能用平方差公式【例题】【例2】计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5). 【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-22-y2-5y+y+5
=-4y+1.1.下列多项式乘法中,能用平方差公式计算的是 ( )
(1)(x+1)(1+x); (2)(a+b)(b-a);
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). (2)(5)(6)【跟踪训练】2.利用平方差公式计算:原式=(-2y-x)(-2y+x)
= 4y2-x2.【解析】原式=(5+2x)(5-2x)
= 25-4x2.【解析】原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x.平方差公式的逆用
a2-b2 = (a+b)(a-b)【解析】 【解析】原式=(0.5-x)(0.5+x)(x2 +0.25)
=( 0.25-x2)( 0.25+x2)
=0.062 5-x4.(5)100.5×99.5.
【解析】原式=(100+0.5)(100-0.5)
=10 000-0.25
=9 999.75.1.(眉山·中考)下列运算中正确的是( )A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 . 2.(威海·中考)已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.3.(湖州·中考)将图甲中阴影部分的小长方形变换到
图乙位置,你能根据两个图形的面积关系得到的数学公式是
___________.
【解析】图甲的面积=(a+b)(a-b),图乙的面积=a(a-
b)+b(a-b)=a2-ab+ab-b2=a2-b2.
答案:(a+b)(a-b)=a2-b2 原式=(100-1)(100+1)×10001
=(10 000-1)(10 000+1)
=100 000 000-1
=99 999 999.4.计算 99×101×10001. 【解析】5.化简:(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16).原式=(x2-y2 )( x2+y2)(x4+y4)(x8+y8)(x16+y16)
=(x4-y4)(x4+y4)(x8+y8)(x16+y16)
=(x8-y8)(x8+y8)(x16+y16)
=(x16-y16)(x16+y16)
= x32-y32.【解析】通过本课时的学习,需要我们掌握:平方差公式:(a+b)(a-b)=a2-b2.即两个数的和与这两个数的差的积,等于这两个数的平方差.平方差公式的逆用: a2-b2 = (a+b)(a-b)我的成功只依赖两条:一条是毫不动摇地坚持到底;一条是用手把脑子里想出的图形一丝不差地制造出来.
——蒙日 (x+1)(x-1); (2) (a+2)(a-2);
(3) (2x+1)(2x-1); (4) (3x+4y)(3x-4y). 观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?等号的左边:两个数的和与差的积,
等号的右边:是这两个数的平方差.计算:
14.2.1 平方差公式数学组:李红娟 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn.多项式与多项式相乘的法则 (x+1)(x-1) (2) (a+2)(a-2);
(3) (2x+1)(2x-1); (4) (3x+4y)(3x-4y). 观察上述算式,你能发现什么共同点?运算出结果后,你发现什么规律?计算: 阅读课本107页,回答以下问题:(时间3分钟)
1、你能从代数和几何两个角度证明公式吗?
2、你用能文字语言表述平方差公式?
3、平方差公式有哪些特征呢?
4、公式中的a、b表示什么呢?
自学提纲代数法:ab几何法几何法(a+b)(a-b)=a2-b2结论: 两个数的和与这两个数的差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2相反为b 相同为a 特征:a,b可以是单项式也可以是多项式.4、公式中的a、b表示什么呢?第一关: ⑴ (3x+2)(3x-2) ;⑵ (b+2a)(2a-b); (3) (-x+2y)(-x-2y);(4) (3m-4n)(-3m-4n);运用平方差公式计算:(5)(6-mn)(mn+6).第二关:下面各式的计算对不对?如果不对,应怎样改正?第三关:计算:第四关:计算:谈谈你的收获:(1)平方差公式是什么?它的文字语言如何叙述?
(2)平方差公式的特征是什么?
(3)应用平方差公式时要注意什么?
(4)本节课使用了哪些数学思想?作业:课本112页第一题1. (1+x)( 1-x)=1- 2. (-3+a)(-3- )= -a24. (0.3x-2)( )=4-0.09 x23. (x+a)(a )=a2 –x25. (ab )( -x)= x2 - 填空:使等式两边满足平方差公式x2a9-x-aba2b2-x第二关: 请从这个正方形纸板上,剪下一个边长为b的小正方形,如图1,拼成如图2的长方形,你能根据图中的面积说明平方差公式吗?(a+b)(a-b)=a2-b2图1图2【例1】运用平方差公式计算:
(1) (3x+2 )( 3x-2 ) .(2) (b+2a)(2a-b). 【解析】 (1) (3x+2)(3x-2)=(3x)2-22=9x2-4.(2)(b+2a)(2a-b)=(2a+b)(2a-b)=(2a)2-b2=4a2-b2.只有符合(a+b) (a- b)的
形式才能用平方差公式【例题】【例2】计算
(1) 102×98. (2)(y+2)(y-2)-(y -1)(y+5). 【解析】
(1) 102×98
=(100+2)(100-2)
=1002-22
=10 000-4
=9 996.(2)原式
=(y2-22)-(y2+5y-y-5)
= y2-22-y2-5y+y+5
=-4y+1.1.下列多项式乘法中,能用平方差公式计算的是 ( )
(1)(x+1)(1+x); (2)(a+b)(b-a);
(3)(-a+b)(a-b); (4)(x2-y)(x+y2);
(5)(-a-b)(a-b); (6)(c2-d2)(d2+c2). (2)(5)(6)【跟踪训练】2.利用平方差公式计算:原式=(-2y-x)(-2y+x)
= 4y2-x2.【解析】原式=(5+2x)(5-2x)
= 25-4x2.【解析】原式=[(x+6)-(x-6)][(x+6)+(x-6)]
= (x+6-x+6)(x+6+x-6)
=12×2x=24x.平方差公式的逆用
a2-b2 = (a+b)(a-b)【解析】 【解析】原式=(0.5-x)(0.5+x)(x2 +0.25)
=( 0.25-x2)( 0.25+x2)
=0.062 5-x4.(5)100.5×99.5.
【解析】原式=(100+0.5)(100-0.5)
=10 000-0.25
=9 999.75.1.(眉山·中考)下列运算中正确的是( )A. B.
C. D.
【解析】选B. 在A中3a+2a=5a;C中 ;
D中 . 2.(威海·中考)已知a-b=1,则a2-b2-2b的值为( )
A.4 B.3 C.1 D.0
【解析】选C.a2-b2-2b=(a-b)(a+b)-2b=a+b-2b=a-b=1.3.(湖州·中考)将图甲中阴影部分的小长方形变换到
图乙位置,你能根据两个图形的面积关系得到的数学公式是
___________.
【解析】图甲的面积=(a+b)(a-b),图乙的面积=a(a-
b)+b(a-b)=a2-ab+ab-b2=a2-b2.
答案:(a+b)(a-b)=a2-b2 原式=(100-1)(100+1)×10001
=(10 000-1)(10 000+1)
=100 000 000-1
=99 999 999.4.计算 99×101×10001. 【解析】5.化简:(x-y)(x+y)(x2+y2)(x4+y4)(x8+y8)(x16+y16).原式=(x2-y2 )( x2+y2)(x4+y4)(x8+y8)(x16+y16)
=(x4-y4)(x4+y4)(x8+y8)(x16+y16)
=(x8-y8)(x8+y8)(x16+y16)
=(x16-y16)(x16+y16)
= x32-y32.【解析】通过本课时的学习,需要我们掌握:平方差公式:(a+b)(a-b)=a2-b2.即两个数的和与这两个数的差的积,等于这两个数的平方差.平方差公式的逆用: a2-b2 = (a+b)(a-b)我的成功只依赖两条:一条是毫不动摇地坚持到底;一条是用手把脑子里想出的图形一丝不差地制造出来.
——蒙日 (x+1)(x-1); (2) (a+2)(a-2);
(3) (2x+1)(2x-1); (4) (3x+4y)(3x-4y). 观察上述算式,你能发现什么规律?运算出结果后,你又发现什么规律?等号的左边:两个数的和与差的积,
等号的右边:是这两个数的平方差.计算:
