第五章 基本平面图形专题训练 线段与角中的折叠与动点(边)问题(含答案)
文档属性
| 名称 | 第五章 基本平面图形专题训练 线段与角中的折叠与动点(边)问题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-31 19:57:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章 基本平面图形
专题训练 线段与角中的折叠与动点(边)问题
一、线段中的折叠问题
1.如图所示,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长是多长
2.如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若则这条绳子的原长是多长
二、线段中的动点问题
3.如图,射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O 出发,沿OM方向以1 cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O 时,点P,Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P,Q两点相遇
(2)当P在线段AB上且PA=3PB时,点Q 运动到的位置恰好是线段AB的三等分点,求点Q的运动速度.
4.已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B,C左侧,C在D左侧).
(1)M,N分别是线段AC,BD的中点,若BC =4,求MN;
(2)当CD运动到D点与B点重合时,P是线段AB延长线上一点,下列两个结论:
是定值; 是定值.
请作出正确的选择,并求出其定值.
三、角中的折叠问题
5.(1)如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.作∠FBD的平分线BE,求∠CBE的度数;
(2)现将∠FBD沿BF折叠使BE,BD落在∠FBC的内部,且折叠后的BE交CF于点M,BD交CF于点N,若BN平分∠CBM,则∠ABC的度数是多少
6.(1)将一张长方形纸片按如图1所示的方式折叠,BC,BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC,BD为折痕,若∠CBD=115°,求 的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC,BD为折痕,若∠CBD=α,求 的度数(用含α的式子表示).
四、角中的动边问题
7.如图,点O在直线AB上,OD平分∠AOB,作射线OE,OF,使得∠AOF=2∠DOE.
(1)当射线OE,OF在如图位置时,试说明:OE平分∠FOB.
(2)当射线OE,OF从图的位置同时绕点O 逆时针旋转,在转动的过程中始终满足∠AOF=2∠DOE,当 时,求∠BOE的度数.
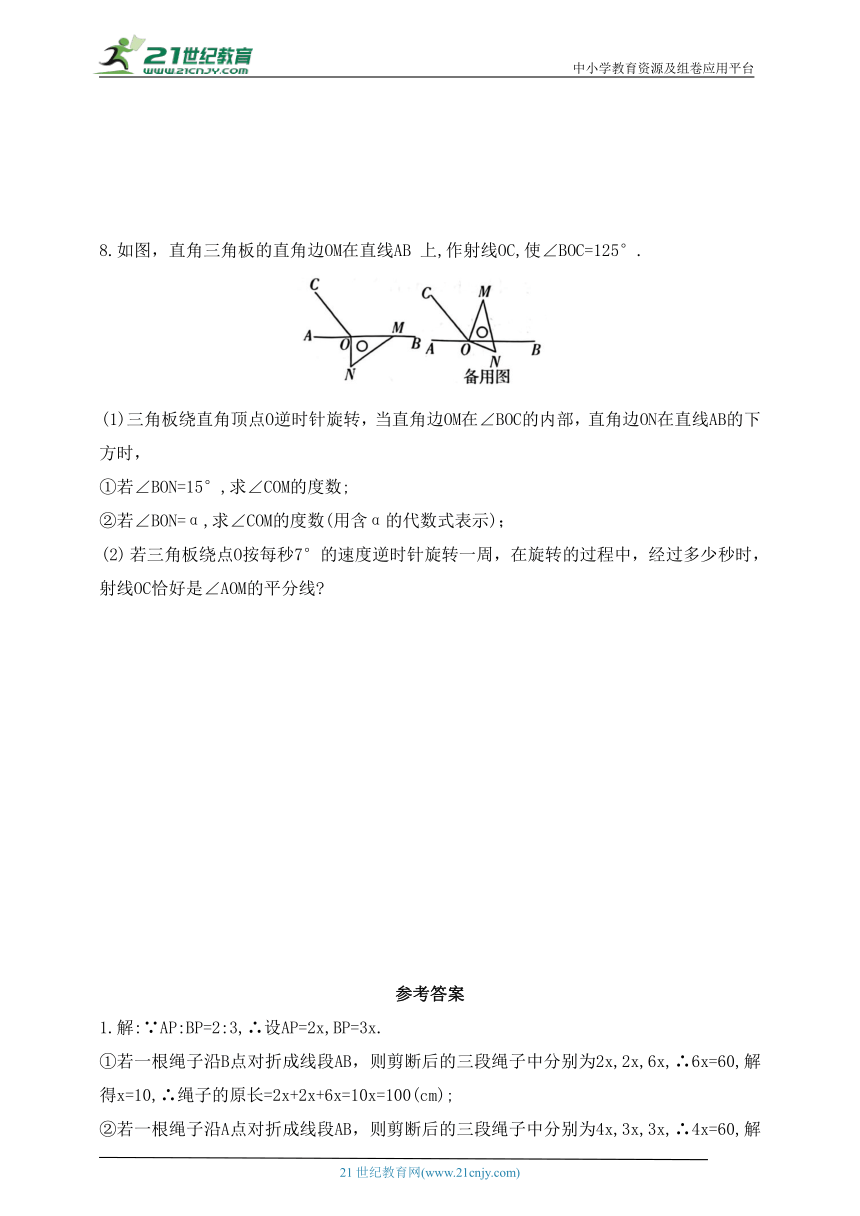
8.如图,直角三角板的直角边OM在直线AB 上,作射线OC,使∠BOC=125°.
(1)三角板绕直角顶点O逆时针旋转,当直角边OM在∠BOC的内部,直角边ON在直线AB的下方时,
①若∠BON=15°,求∠COM的度数;
②若∠BON=α,求∠COM的度数(用含α的代数式表示);
若三角板绕点O按每秒7°的速度逆时针旋转一周,在旋转的过程中,经过多少秒时,射线OC恰好是∠AOM的平分线
参考答案
1.解:∵AP:BP=2:3,∴设AP=2x,BP=3x.
①若一根绳子沿B点对折成线段AB,则剪断后的三段绳子中分别为2x,2x,6x,∴6x=60,解得x=10,∴绳子的原长=2x+2x+6x=10x=100(cm);
②若一根绳子沿A点对折成线段AB,则剪断后的三段绳子中分别为4x,3x,3x,∴4x=60,解得x=15,∴绳子的原长=4x+3x+3x=10x=150(cm).
综上所述,绳子的原长为100cm或150cm.
2.解:①当NP的2倍最短时,得NP=30cm,
∴MN=NP+MP=48cm,∴这条绳子的原长为2MN=96cm,
此情况不符合题意,故舍去;
②当MP最短时,得MP=60cm,
∴MN=MP+NP=160cm,
∴这条绳子的原长为2MN=320cm;
③当NP最短时,得NP=60cm,
∴MN=MP+NP=96cm,
∴这条绳子的原长为2MN=192cm.
④当MP的2倍最短时,得MP=30cm,NP=50cm.MN=MP+NP=80cm
∴这条绳子的原长为2MN=160cm.
综上所述,这条绳子的原长为320cm或192cm或160cm.
3.解:(1)设经过t秒时间P,Q两点相遇,
则t+2t=90,解得t=30,
所以经过30秒时间P,Q两点相遇.
(2)∵AB=60cm,PA=3PB,∴PA=45cm,OP=65cm.∴点P,Q的运动时间为65秒,
∴QB=20cm或40cm,
∴点Q是速度为 或
4.解:(1)如图1,
∵M,N分别为线段AC,BD的中点,
∴MN=AD-AM-DN=9.
如图2,∵M,N分别为线段AC,BD的中点,
∴MN=AD-AM-DN=12+6-4-4-1=9.
(2)①正确,理由如下:
是定值2.
5.解:(1)由折叠知:
∵BE平分
∵∠ABF+∠FBD=180°,
(2)如图,设∠DBE=∠EBF=x.是由∠FBD沿BF翻折得到,
∴∠MBF=∠MBN=x.∴∠CBN=∠MBN=x,
∵BN平分∠CBM,∴∠CBF=3x.
∵△CBF是由△CBA翻折得到,∴∠ABC=∠CBF=3x.
∵∠ABF+∠FBD=180°,∴8x=180°,解得x=22.5°,∴∠ABC=3x=67.5°.
6.解:(1)由题意知:
(2)∵∠CBD=115°,∴∠ABC+∠EBD=180°-115°=65°.
(3)∵∠CBD=α,∴∠ABC+∠EBD=180°-α.
=360°-2α-180°=180°-2a.
7.解:(1)∵点O在直线AB上,OD平分∠AOB,∴∠AOD=∠BOD=90°.
又∵∠AOF=2∠DOE,设∠DOE=x°,则∠AOF=2x°,
∴∠BOE=∠BOD-∠DOE=(90-x)°,
∠EOF=∠DOE+∠DOF=∠DOE+(∠AOD-∠AOF)=x°+(90°-2x°)=(90-x)°,
∴∠BOE=∠EOF=(90-x)°,即OE平分∠FOB.
(2)①如图1,当 时,
则∠DOF=2∠DOE=2x°,∴∠AOF+∠DOF=2x°+2x°=90°,解得x=22.5°,
∴∠BOE=∠BOD-∠DOE=90°-22.5°=67.5°;
②如图2,当 时,则∠AOE=∠DOE=x°,
∠AOD=90°=∠AOE+∠DOE=x°+x°,解得x=45°,
∴∠BOE=∠BOD+∠DOE=90°+45°=135°.
综上所述,∠BOE的度数为67.5°或135°.
8.解:(1)①∵∠BON=15°,∠MON=90°,
∴∠BOM=90°-15°=75°.
又
②∵∠BOC=125°,∠MON=90°,
∴∠BOM=125°-∠COM,∠BOM=90°-∠BON,
∴125°-∠COM=90°-∠BON.
又∵∠BON=α,∴∠COM=α+35°.
(2)∵∠BOC=125°,∴∠AOC=55°.
当直线OC恰好平分∠AOM时,
∠COM=∠AOC=55°,∴∠BOM=125°-55°=70°,
此时,三角板旋转的角度为70°,
∴旋转时间为70°÷7°=10(秒).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 基本平面图形
专题训练 线段与角中的折叠与动点(边)问题
一、线段中的折叠问题
1.如图所示,把一根绳子对折成线段AB,从点P处把绳子剪断,已知AP:BP=2:3,若剪断后的各段绳子中最长的一段为60cm,则绳子的原长是多长
2.如图,将一根绳子对折后用线段MN表示,现从P处将绳子剪断,剪断后的各段绳子中较短的一段为60cm,若则这条绳子的原长是多长
二、线段中的动点问题
3.如图,射线OM上有三点A,B,C,满足OA=20cm,AB=60cm,BC=10cm,点P从点O 出发,沿OM方向以1 cm/秒的速度匀速运动,点Q从点C出发在线段CO上向点O匀速运动,两点同时出发,当点Q运动到点O 时,点P,Q停止运动.
(1)若点Q运动速度为2cm/秒,经过多长时间P,Q两点相遇
(2)当P在线段AB上且PA=3PB时,点Q 运动到的位置恰好是线段AB的三等分点,求点Q的运动速度.
4.已知线段AB=12,CD=6,线段CD在直线AB上运动(A在B,C左侧,C在D左侧).
(1)M,N分别是线段AC,BD的中点,若BC =4,求MN;
(2)当CD运动到D点与B点重合时,P是线段AB延长线上一点,下列两个结论:
是定值; 是定值.
请作出正确的选择,并求出其定值.
三、角中的折叠问题
5.(1)如图,将长方形纸片的一角折叠,使顶点A落在F处,折痕为BC.作∠FBD的平分线BE,求∠CBE的度数;
(2)现将∠FBD沿BF折叠使BE,BD落在∠FBC的内部,且折叠后的BE交CF于点M,BD交CF于点N,若BN平分∠CBM,则∠ABC的度数是多少
6.(1)将一张长方形纸片按如图1所示的方式折叠,BC,BD为折痕,求∠CBD的度数;
(2)将一张长方形纸片按如图2所示的方式折叠,BC,BD为折痕,若∠CBD=115°,求 的度数;
(3)将一张长方形纸片按如图3所示的方式折叠,BC,BD为折痕,若∠CBD=α,求 的度数(用含α的式子表示).
四、角中的动边问题
7.如图,点O在直线AB上,OD平分∠AOB,作射线OE,OF,使得∠AOF=2∠DOE.
(1)当射线OE,OF在如图位置时,试说明:OE平分∠FOB.
(2)当射线OE,OF从图的位置同时绕点O 逆时针旋转,在转动的过程中始终满足∠AOF=2∠DOE,当 时,求∠BOE的度数.
8.如图,直角三角板的直角边OM在直线AB 上,作射线OC,使∠BOC=125°.
(1)三角板绕直角顶点O逆时针旋转,当直角边OM在∠BOC的内部,直角边ON在直线AB的下方时,
①若∠BON=15°,求∠COM的度数;
②若∠BON=α,求∠COM的度数(用含α的代数式表示);
若三角板绕点O按每秒7°的速度逆时针旋转一周,在旋转的过程中,经过多少秒时,射线OC恰好是∠AOM的平分线
参考答案
1.解:∵AP:BP=2:3,∴设AP=2x,BP=3x.
①若一根绳子沿B点对折成线段AB,则剪断后的三段绳子中分别为2x,2x,6x,∴6x=60,解得x=10,∴绳子的原长=2x+2x+6x=10x=100(cm);
②若一根绳子沿A点对折成线段AB,则剪断后的三段绳子中分别为4x,3x,3x,∴4x=60,解得x=15,∴绳子的原长=4x+3x+3x=10x=150(cm).
综上所述,绳子的原长为100cm或150cm.
2.解:①当NP的2倍最短时,得NP=30cm,
∴MN=NP+MP=48cm,∴这条绳子的原长为2MN=96cm,
此情况不符合题意,故舍去;
②当MP最短时,得MP=60cm,
∴MN=MP+NP=160cm,
∴这条绳子的原长为2MN=320cm;
③当NP最短时,得NP=60cm,
∴MN=MP+NP=96cm,
∴这条绳子的原长为2MN=192cm.
④当MP的2倍最短时,得MP=30cm,NP=50cm.MN=MP+NP=80cm
∴这条绳子的原长为2MN=160cm.
综上所述,这条绳子的原长为320cm或192cm或160cm.
3.解:(1)设经过t秒时间P,Q两点相遇,
则t+2t=90,解得t=30,
所以经过30秒时间P,Q两点相遇.
(2)∵AB=60cm,PA=3PB,∴PA=45cm,OP=65cm.∴点P,Q的运动时间为65秒,
∴QB=20cm或40cm,
∴点Q是速度为 或
4.解:(1)如图1,
∵M,N分别为线段AC,BD的中点,
∴MN=AD-AM-DN=9.
如图2,∵M,N分别为线段AC,BD的中点,
∴MN=AD-AM-DN=12+6-4-4-1=9.
(2)①正确,理由如下:
是定值2.
5.解:(1)由折叠知:
∵BE平分
∵∠ABF+∠FBD=180°,
(2)如图,设∠DBE=∠EBF=x.是由∠FBD沿BF翻折得到,
∴∠MBF=∠MBN=x.∴∠CBN=∠MBN=x,
∵BN平分∠CBM,∴∠CBF=3x.
∵△CBF是由△CBA翻折得到,∴∠ABC=∠CBF=3x.
∵∠ABF+∠FBD=180°,∴8x=180°,解得x=22.5°,∴∠ABC=3x=67.5°.
6.解:(1)由题意知:
(2)∵∠CBD=115°,∴∠ABC+∠EBD=180°-115°=65°.
(3)∵∠CBD=α,∴∠ABC+∠EBD=180°-α.
=360°-2α-180°=180°-2a.
7.解:(1)∵点O在直线AB上,OD平分∠AOB,∴∠AOD=∠BOD=90°.
又∵∠AOF=2∠DOE,设∠DOE=x°,则∠AOF=2x°,
∴∠BOE=∠BOD-∠DOE=(90-x)°,
∠EOF=∠DOE+∠DOF=∠DOE+(∠AOD-∠AOF)=x°+(90°-2x°)=(90-x)°,
∴∠BOE=∠EOF=(90-x)°,即OE平分∠FOB.
(2)①如图1,当 时,
则∠DOF=2∠DOE=2x°,∴∠AOF+∠DOF=2x°+2x°=90°,解得x=22.5°,
∴∠BOE=∠BOD-∠DOE=90°-22.5°=67.5°;
②如图2,当 时,则∠AOE=∠DOE=x°,
∠AOD=90°=∠AOE+∠DOE=x°+x°,解得x=45°,
∴∠BOE=∠BOD+∠DOE=90°+45°=135°.
综上所述,∠BOE的度数为67.5°或135°.
8.解:(1)①∵∠BON=15°,∠MON=90°,
∴∠BOM=90°-15°=75°.
又
②∵∠BOC=125°,∠MON=90°,
∴∠BOM=125°-∠COM,∠BOM=90°-∠BON,
∴125°-∠COM=90°-∠BON.
又∵∠BON=α,∴∠COM=α+35°.
(2)∵∠BOC=125°,∴∠AOC=55°.
当直线OC恰好平分∠AOM时,
∠COM=∠AOC=55°,∴∠BOM=125°-55°=70°,
此时,三角板旋转的角度为70°,
∴旋转时间为70°÷7°=10(秒).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
