力与运动——抛体运动(学案)-2023年新高考物理二轮复习专题讲义
文档属性
| 名称 | 力与运动——抛体运动(学案)-2023年新高考物理二轮复习专题讲义 |
|
|
| 格式 | docx | ||
| 文件大小 | 436.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 21:41:05 | ||
图片预览


文档简介
抛体运动
平抛运动规律及应用
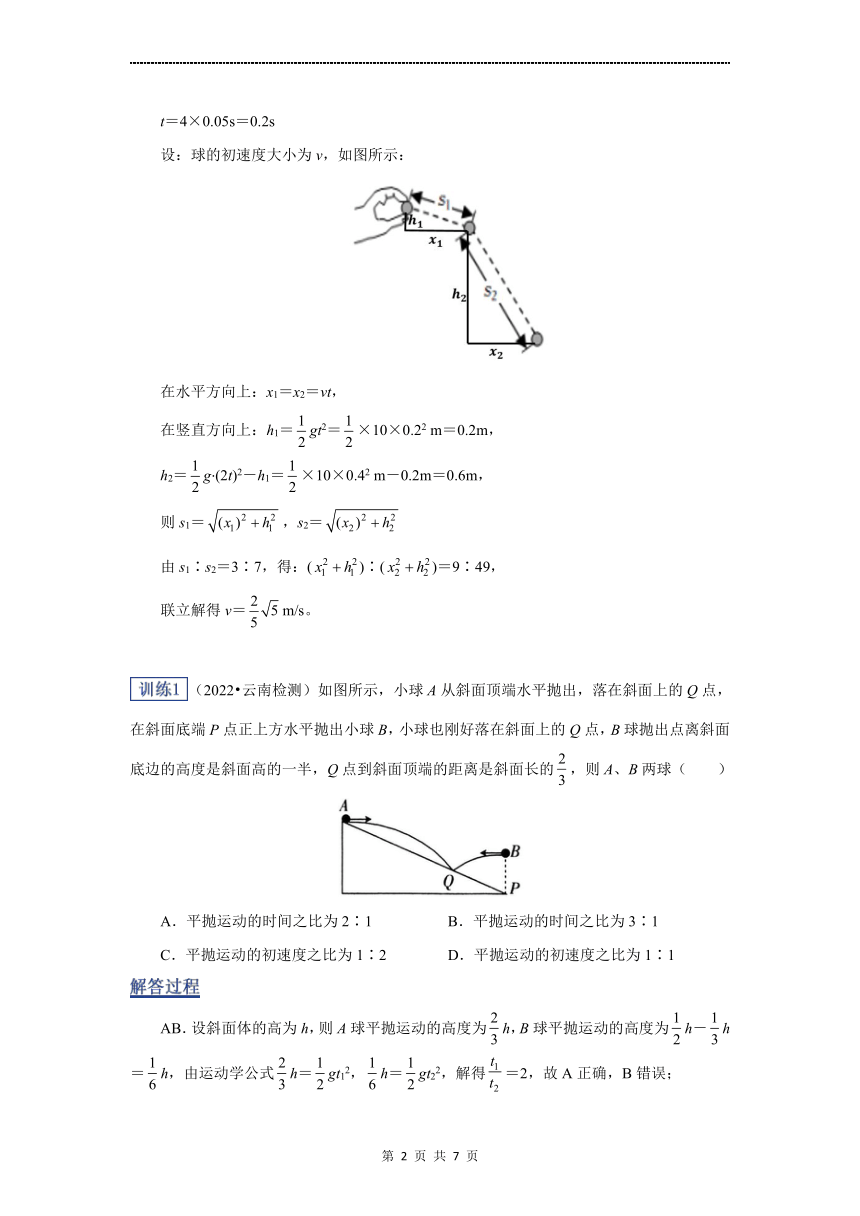
(2022 全国甲卷)将一小球水平抛出,使用频闪仪和照相机对运动的小球进行拍摄,频闪仪每隔0.05 s发出一次闪光。某次拍摄时,小球在抛出瞬间频闪仪恰好闪光,拍摄的照片编辑后如图所示。图中的第一个小球为抛出瞬间的影像,每相邻两个球之间被删去了3个影像,所标出的两个线段的长度s1和s2之比为3∶7。重力加速度大小取g=10 m/s2,忽略空气阻力。求在抛出瞬间小球速度的大小。
关键信息:水平抛出、忽略空气阻力 → 平抛运动模型
每隔0.05 s发出一次闪光、每相邻两个球之间删去了3个影像 → 两段位移S1和S2的运动时间相等,(易错点)每段位移的时间间隔为4×0.05s=0.2s。
解题思路:已知两段位移s1和s2之比为3∶7,则只要表示出平抛运动的两段位移,即可由位移的比例关系求解。
相邻两球之间有三个影像被删,说明有四段间隙,所以图中两球间隔时间:
t=4×0.05s=0.2s
设:球的初速度大小为v,如图所示:
在水平方向上:x1=x2=vt,
在竖直方向上:h1=gt2=×10×0.22 m=0.2m,
h2=g (2t)2-h1=×10×0.42 m-0.2m=0.6m,
则s1=,s2=
由s1∶s2=3∶7,得:()∶()=9∶49,
联立解得v=m/s。
(2022 云南检测)如图所示,小球A从斜面顶端水平抛出,落在斜面上的Q点,在斜面底端P点正上方水平抛出小球B,小球也刚好落在斜面上的Q点,B球抛出点离斜面底边的高度是斜面高的一半,Q点到斜面顶端的距离是斜面长的,则A、B两球( )
A.平抛运动的时间之比为2∶1 B.平抛运动的时间之比为3∶1
C.平抛运动的初速度之比为1∶2 D.平抛运动的初速度之比为1∶1
AB.设斜面体的高为h,则A球平抛运动的高度为h,B球平抛运动的高度为h-h=h,由运动学公式h=gt12,h=gt22,解得=2,故A正确,B错误;
CD.AB两球平抛运动的水平位移之比为2∶1,由v=可知,平抛运动的初速度之比为=1,故C错误,D正确。故选AD。
1.多体平抛问题处理思路
(1)若两物体同时从同一高度(或同一点)抛出,则两物体始终在同一高度,二者间距只取决于两物体的水平分运动。
(2)若两物体同时从不同高度抛出,则两物体高度差始终与抛出点高度差相同,二者间距由两物体的水平分运动和竖直高度差决定。
(3)若两物体从同一点先后抛出,两物体竖直高度差随时间均匀增大,二者间距取决于两物体的水平分运动和竖直分运动。
(4)两条平抛运动轨迹的相交处是两物体的可能相遇处,两物体要在此处相遇,必须同时到达此处。
2.做平抛运动的物体,落点不在水平面上,而是在斜面、竖直面、弧面上时,将平抛运动的知识与几何知识结合起来,分解速度或分解位移,在水平方向和竖直方向分别列式求解。
斜抛运动
(2022 山东模拟)2022年2月8日,18岁的中国选手谷爱凌在北京冬奥会自由式滑雪女子大跳台比赛中以绝对优势夺得金牌,这是中国代表团在北京冬奥会上的第三枚金牌,被誉为“雪上公主”的她赛后喜极而泣。现将比赛某段过程简化成如图可视为质点小球的运动,小球从倾角为α=30°的斜面顶端O点以v0飞出,已知v0=20m/s,且与斜面的夹角为θ=60°。图中虚线为小球在空中的运动轨迹,且A为轨迹上离斜面最远的点,B为小球在斜面上的落点,C是过A作竖直线与斜面的交点,不计空气阻力,重力加速度g=10m/s2。求:
(1)小球从O运动到A点所用时间t;
(2)小球离斜面最远的距离L;
(3)O、C两点间距离x。
关键信息:从O点以v0飞出,且v0与斜面的夹角为θ=60° → 斜抛运动模型
A为轨迹上离斜面最远的点 → 在A点垂直斜面方向的分速度为零
解题思路:将斜抛运动在沿斜面方向和垂直斜面方向进行分解。
该斜抛运动在垂直斜面方向的运动具有对称性,即O点到A点所用时间与A点到B点所用时间相等。
将速度和加速度进行如图所示分解:
垂直斜面方向v1=v0 sinθ,a1=gcosα
当垂直斜面方向的分速度为零时(速度方向平行斜面),离斜面最远。
t= 解得:t=2s;
(2)垂直斜面方向v1匀减速至0时,由L=,
代入数据得:L=10m;
(3)
由垂直斜面方向运动对称性可得小球从0到A与从A到B所用时间相等
平行斜面方向:a2=gsinα,v2=v0 cosθ
lOB=v2 2t+a2(2t)2
将小球的运动按水平方向和竖直方向分解,小球在水平方向做匀速直线运动,
由于 tOA=tOB=t,在水平方向有:xOA=xOB,由此可知C为OB中点,则:x=lOB
代入数据解得:x=40 m;
将小球的运动按水平方向和竖直方向分解,水平方向的分速度v0x=v0 cos(θ-α)
由匀速直线运动规律得:xOA=v0 cos(θ-α)t;
由几何关系知:x= 解得:x=40m。
(2022 山东高考)如图所示,某同学将离地1.25m的网球以13m/s的速度斜向上击出,击球点到竖直墙壁的距离4.8m。当网球竖直分速度为零时,击中墙壁上离地高度为8.45m的P点。网球与墙壁碰撞后,垂直墙面速度分量大小变为碰前的0.75倍。平行墙面的速度分量不变。重力加速度g取10m/s2,网球碰墙后的速度大小v和着地点到墙壁的距离d分别为( )
A.v=5m/s B.v=m/s C.d=3.6m D.d=3.9m
设网球被击出时的初速度为v0,沿垂直墙面的方向分速度为v0⊥,沿平行墙面的分速度为v0//,竖直方向的分速度为v0y,则
对竖直方向,由竖直上抛运动的规律得:=2g(H-h)
代入数据得v0y=m/s=12m/s
网球被击出到击中墙壁经历的时间t==s=1.2s
对垂直墙面的方向,由匀速运动规律得:v0⊥= m/s=4 m/s
由运动的合成分解知:v0//==3m/s
反弹后,垂直墙面的速度分量=0.75·v0⊥=3m/s
则反弹后的网球速度大小为v==m/s
网球落到地面的时间t′==s=1.3s
着地点到墙壁的距离d=v′0⊥t′=3.9m,故选BD。
1.斜抛运动至最高点时速度水平,可采取用逆向思维法,看作反方向的平抛运动。斜抛运动往往以最高点为临界点时具有时间上的对称性。
2.求解方法
(1)常规分解法:将斜抛运动分解为沿水平方向的匀速直线运动和竖直方向的匀变速直线运动。
(2)特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度g分解为gx、gy,初速度v0分解为vx、vy,然后分别在x、y方向上列方程求解。
平抛运动规律及应用
(2022 全国甲卷)将一小球水平抛出,使用频闪仪和照相机对运动的小球进行拍摄,频闪仪每隔0.05 s发出一次闪光。某次拍摄时,小球在抛出瞬间频闪仪恰好闪光,拍摄的照片编辑后如图所示。图中的第一个小球为抛出瞬间的影像,每相邻两个球之间被删去了3个影像,所标出的两个线段的长度s1和s2之比为3∶7。重力加速度大小取g=10 m/s2,忽略空气阻力。求在抛出瞬间小球速度的大小。
关键信息:水平抛出、忽略空气阻力 → 平抛运动模型
每隔0.05 s发出一次闪光、每相邻两个球之间删去了3个影像 → 两段位移S1和S2的运动时间相等,(易错点)每段位移的时间间隔为4×0.05s=0.2s。
解题思路:已知两段位移s1和s2之比为3∶7,则只要表示出平抛运动的两段位移,即可由位移的比例关系求解。
相邻两球之间有三个影像被删,说明有四段间隙,所以图中两球间隔时间:
t=4×0.05s=0.2s
设:球的初速度大小为v,如图所示:
在水平方向上:x1=x2=vt,
在竖直方向上:h1=gt2=×10×0.22 m=0.2m,
h2=g (2t)2-h1=×10×0.42 m-0.2m=0.6m,
则s1=,s2=
由s1∶s2=3∶7,得:()∶()=9∶49,
联立解得v=m/s。
(2022 云南检测)如图所示,小球A从斜面顶端水平抛出,落在斜面上的Q点,在斜面底端P点正上方水平抛出小球B,小球也刚好落在斜面上的Q点,B球抛出点离斜面底边的高度是斜面高的一半,Q点到斜面顶端的距离是斜面长的,则A、B两球( )
A.平抛运动的时间之比为2∶1 B.平抛运动的时间之比为3∶1
C.平抛运动的初速度之比为1∶2 D.平抛运动的初速度之比为1∶1
AB.设斜面体的高为h,则A球平抛运动的高度为h,B球平抛运动的高度为h-h=h,由运动学公式h=gt12,h=gt22,解得=2,故A正确,B错误;
CD.AB两球平抛运动的水平位移之比为2∶1,由v=可知,平抛运动的初速度之比为=1,故C错误,D正确。故选AD。
1.多体平抛问题处理思路
(1)若两物体同时从同一高度(或同一点)抛出,则两物体始终在同一高度,二者间距只取决于两物体的水平分运动。
(2)若两物体同时从不同高度抛出,则两物体高度差始终与抛出点高度差相同,二者间距由两物体的水平分运动和竖直高度差决定。
(3)若两物体从同一点先后抛出,两物体竖直高度差随时间均匀增大,二者间距取决于两物体的水平分运动和竖直分运动。
(4)两条平抛运动轨迹的相交处是两物体的可能相遇处,两物体要在此处相遇,必须同时到达此处。
2.做平抛运动的物体,落点不在水平面上,而是在斜面、竖直面、弧面上时,将平抛运动的知识与几何知识结合起来,分解速度或分解位移,在水平方向和竖直方向分别列式求解。
斜抛运动
(2022 山东模拟)2022年2月8日,18岁的中国选手谷爱凌在北京冬奥会自由式滑雪女子大跳台比赛中以绝对优势夺得金牌,这是中国代表团在北京冬奥会上的第三枚金牌,被誉为“雪上公主”的她赛后喜极而泣。现将比赛某段过程简化成如图可视为质点小球的运动,小球从倾角为α=30°的斜面顶端O点以v0飞出,已知v0=20m/s,且与斜面的夹角为θ=60°。图中虚线为小球在空中的运动轨迹,且A为轨迹上离斜面最远的点,B为小球在斜面上的落点,C是过A作竖直线与斜面的交点,不计空气阻力,重力加速度g=10m/s2。求:
(1)小球从O运动到A点所用时间t;
(2)小球离斜面最远的距离L;
(3)O、C两点间距离x。
关键信息:从O点以v0飞出,且v0与斜面的夹角为θ=60° → 斜抛运动模型
A为轨迹上离斜面最远的点 → 在A点垂直斜面方向的分速度为零
解题思路:将斜抛运动在沿斜面方向和垂直斜面方向进行分解。
该斜抛运动在垂直斜面方向的运动具有对称性,即O点到A点所用时间与A点到B点所用时间相等。
将速度和加速度进行如图所示分解:
垂直斜面方向v1=v0 sinθ,a1=gcosα
当垂直斜面方向的分速度为零时(速度方向平行斜面),离斜面最远。
t= 解得:t=2s;
(2)垂直斜面方向v1匀减速至0时,由L=,
代入数据得:L=10m;
(3)
由垂直斜面方向运动对称性可得小球从0到A与从A到B所用时间相等
平行斜面方向:a2=gsinα,v2=v0 cosθ
lOB=v2 2t+a2(2t)2
将小球的运动按水平方向和竖直方向分解,小球在水平方向做匀速直线运动,
由于 tOA=tOB=t,在水平方向有:xOA=xOB,由此可知C为OB中点,则:x=lOB
代入数据解得:x=40 m;
将小球的运动按水平方向和竖直方向分解,水平方向的分速度v0x=v0 cos(θ-α)
由匀速直线运动规律得:xOA=v0 cos(θ-α)t;
由几何关系知:x= 解得:x=40m。
(2022 山东高考)如图所示,某同学将离地1.25m的网球以13m/s的速度斜向上击出,击球点到竖直墙壁的距离4.8m。当网球竖直分速度为零时,击中墙壁上离地高度为8.45m的P点。网球与墙壁碰撞后,垂直墙面速度分量大小变为碰前的0.75倍。平行墙面的速度分量不变。重力加速度g取10m/s2,网球碰墙后的速度大小v和着地点到墙壁的距离d分别为( )
A.v=5m/s B.v=m/s C.d=3.6m D.d=3.9m
设网球被击出时的初速度为v0,沿垂直墙面的方向分速度为v0⊥,沿平行墙面的分速度为v0//,竖直方向的分速度为v0y,则
对竖直方向,由竖直上抛运动的规律得:=2g(H-h)
代入数据得v0y=m/s=12m/s
网球被击出到击中墙壁经历的时间t==s=1.2s
对垂直墙面的方向,由匀速运动规律得:v0⊥= m/s=4 m/s
由运动的合成分解知:v0//==3m/s
反弹后,垂直墙面的速度分量=0.75·v0⊥=3m/s
则反弹后的网球速度大小为v==m/s
网球落到地面的时间t′==s=1.3s
着地点到墙壁的距离d=v′0⊥t′=3.9m,故选BD。
1.斜抛运动至最高点时速度水平,可采取用逆向思维法,看作反方向的平抛运动。斜抛运动往往以最高点为临界点时具有时间上的对称性。
2.求解方法
(1)常规分解法:将斜抛运动分解为沿水平方向的匀速直线运动和竖直方向的匀变速直线运动。
(2)特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度g分解为gx、gy,初速度v0分解为vx、vy,然后分别在x、y方向上列方程求解。
同课章节目录
