力与运动——圆周运动(学案)-2023年新高考物理二轮复习专题讲义
文档属性
| 名称 | 力与运动——圆周运动(学案)-2023年新高考物理二轮复习专题讲义 |  | |
| 格式 | docx | ||
| 文件大小 | 627.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 21:43:20 | ||
图片预览


文档简介
圆周运动
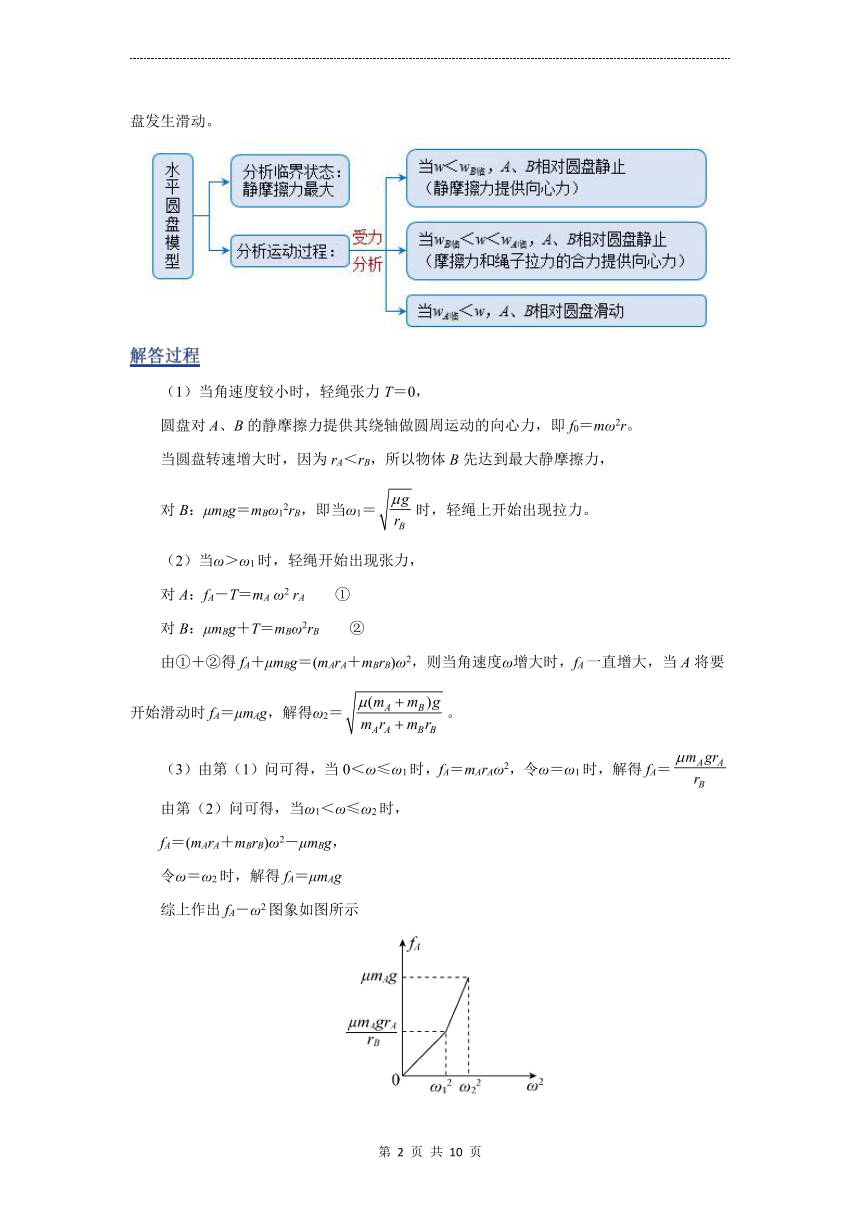
水平面内圆周运动及临界问题
(2021.湖北.检测)水平圆盘上沿直径方向放置以轻绳相连的两个小物块A和B,两物块的质量分别为mA和mB,到圆心的距离分别为rA和rB,且rA<rB。两物块与圆盘间的最大静摩擦力均为自身重力的μ倍,重力加速度为g。忽略小物块A、B的大小,不考虑轻绳拉力上限,轻绳伸直且最初拉力为零。圆盘绕过圆心的竖直轴转动,转动的角速度ω由零缓慢增大。
(1)当圆盘以角速度ω1匀速转动时,轻绳上开始出现拉力,求ω1的大小;
(2)当圆盘以角速度ω2匀速转动时,小物块A将开始滑动,求ω2的大小;
(3)在角速度从零缓慢地增加到小物块A将开始滑动过程中,小物块A与圆盘间摩擦力大小为fA,试通过计算,在坐标系中作出fA-ω2图象(要求:必须标出每段图象转折点的纵坐标值)。
关键信息:、随圆盘一起绕过圆心的竖直轴转动 → 水平圆盘模型
A、B随圆盘一起绕过圆心的竖直轴转动 → 水平圆盘模型
rA<rB,且圆盘转速逐渐增大 → 物块滑动的临界状态为,则,,故wB临<wA临,即B比A先达到临界状态。
解题思路:抓住A刚要滑动和B刚要滑动时的两个临界状态,B所受的静摩擦力刚好达最大值时,细绳刚开始有拉力;A所受的静摩擦力刚好到达最大值时,A、B刚好同时相对圆盘发生滑动。
(1)当角速度较小时,轻绳张力T=0,
圆盘对A、B的静摩擦力提供其绕轴做圆周运动的向心力,即f0=mω2r。
当圆盘转速增大时,因为rA<rB,所以物体B先达到最大静摩擦力,
对B:μmBg=mBω12rB,即当ω1=时,轻绳上开始出现拉力。
(2)当ω>ω1时,轻绳开始出现张力,
对A:fA-T=mA ω2 rA ①
对B:μmBg+T=mBω2rB ②
由①+②得fA+μmBg=(mArA+mBrB)ω2,则当角速度ω增大时,fA一直增大,当A将要开始滑动时fA=μmAg,解得ω2=。
(3)由第(1)问可得,当0<ω≤ω1时,fA=mArAω2,令ω=ω1时,解得fA=
由第(2)问可得,当ω1<ω≤ω2时,
fA=(mArA+mBrB)ω2-μmBg,
令ω=ω2时,解得fA=μmAg
综上作出fA-ω2图象如图所示
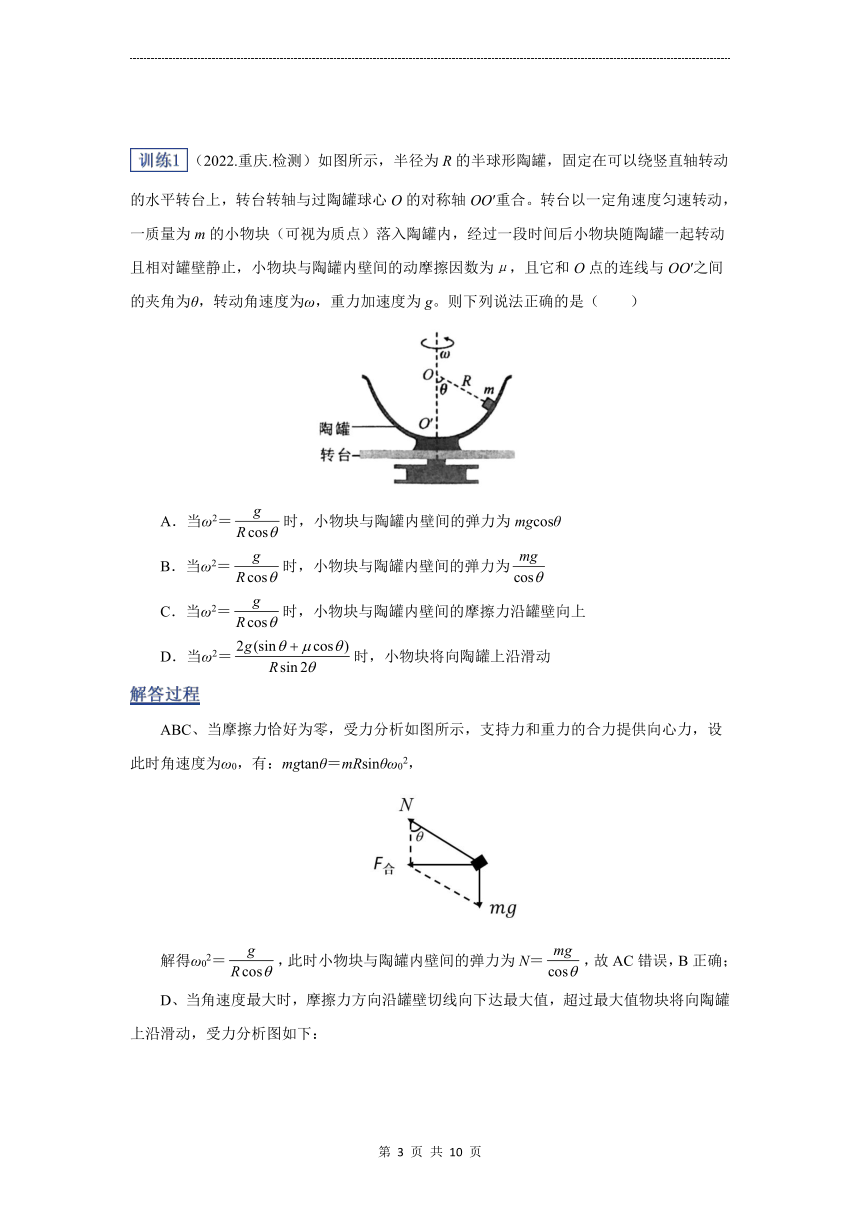
(2022.重庆.检测)如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度匀速转动,一质量为m的小物块(可视为质点)落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,小物块与陶罐内壁间的动摩擦因数为μ,且它和O点的连线与OO′之间的夹角为θ,转动角速度为ω,重力加速度为g。则下列说法正确的是( )
A.当ω2=时,小物块与陶罐内壁间的弹力为mgcosθ
B.当ω2=时,小物块与陶罐内壁间的弹力为
C.当ω2=时,小物块与陶罐内壁间的摩擦力沿罐壁向上
D.当ω2=时,小物块将向陶罐上沿滑动
ABC、当摩擦力恰好为零,受力分析如图所示,支持力和重力的合力提供向心力,设此时角速度为ω0,有:mgtanθ=mRsinθω02,
解得ω02=,此时小物块与陶罐内壁间的弹力为N=,故AC错误,B正确;
D、当角速度最大时,摩擦力方向沿罐壁切线向下达最大值,超过最大值物块将向陶罐上沿滑动,受力分析图如下:
设此最大角速度为ω,
水平方向:fcosθ+Nsinθ=mRsinθω2,
竖直方向:fsinθ+mg=Ncosθ,其中f=μN,
联立解得ω2=,D错误,故选B。
水平面内圆周运动常见的三种临界情况分析:
临界情况 典型模型 临界条件分析
相对滑动的临界条件 两物体相对静止且存在着摩擦力时,二者相对滑动的临界条件是静摩擦力刚好达到最大值
接触与分离的临界条件 两物体恰好接触或分离,临界条件是弹力Fn=0
绳子断裂与松弛的临界条件 绳子所能承受的张力是有限度的,绳子恰不断裂的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛的临界条件是绳子张力为0
竖直面内圆周运动及临界问题
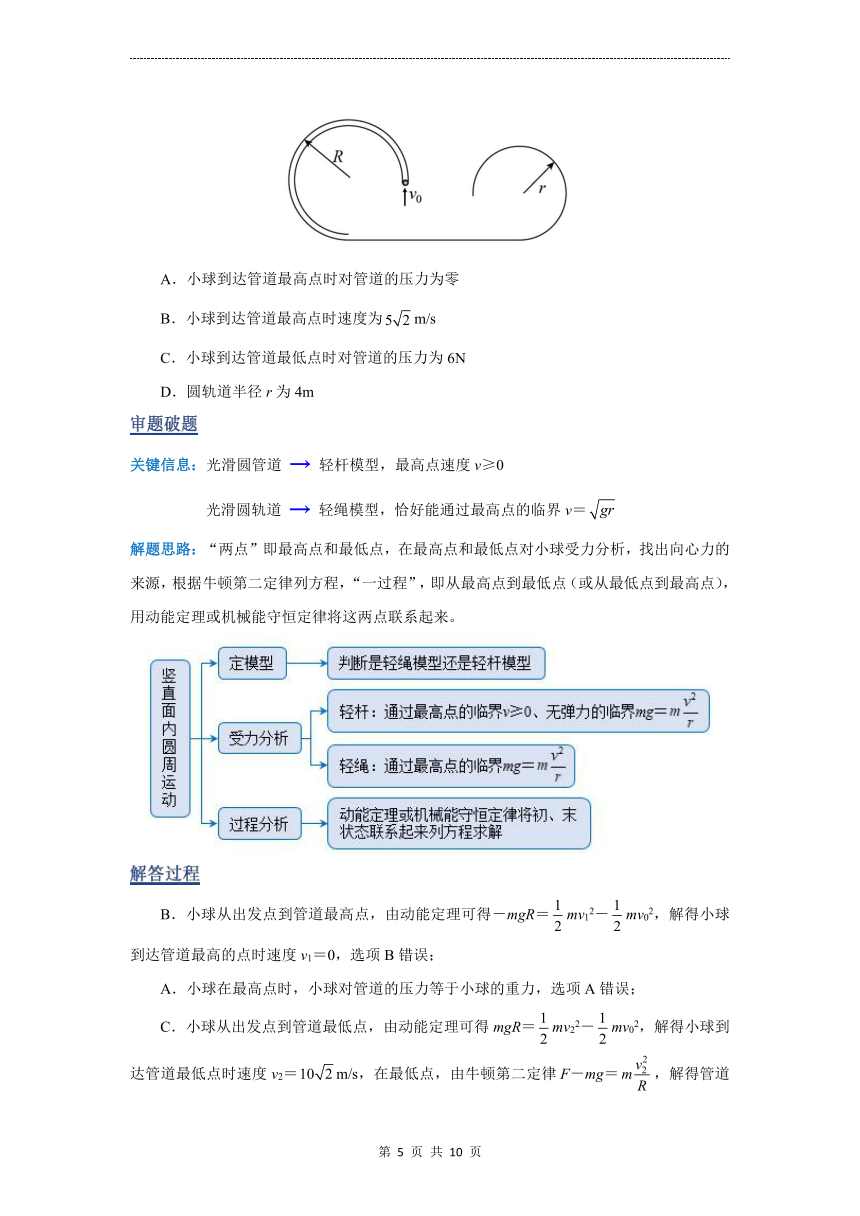
(2022.海南.检测) 如图所示,一质量为m=0.1kg的小球以竖直向上的初速度v0=10m/s冲入一管道。该管道为圆管道,半径为R=5m。已知小球的入口与圆心在同一高度。经过管道后,它又沿着水平导轨进入另一半径为r的圆轨道,且恰好能通过圆轨道的最高点,若所有衔接处均不损失机械能,不计摩擦,小球直径以及管道内径可忽略,圆轨道和圆轨道底端均与水平导轨相切,g取10 m/s2。下列说法正确的是( )
A.小球到达管道最高点时对管道的压力为零
B.小球到达管道最高点时速度为m/s
C.小球到达管道最低点时对管道的压力为6N
D.圆轨道半径r为4m
关键信息:光滑圆管道 → 轻杆模型,最高点速度v≥0
光滑圆轨道 → 轻绳模型,恰好能通过最高点的临界v=
解题思路:“两点”即最高点和最低点,在最高点和最低点对小球受力分析,找出向心力的来源,根据牛顿第二定律列方程,“一过程”,即从最高点到最低点(或从最低点到最高点),用动能定理或机械能守恒定律将这两点联系起来。
B.小球从出发点到管道最高点,由动能定理可得-mgR=mv12-mv02,解得小球到达管道最高的点时速度v1=0,选项B错误;
A.小球在最高点时,小球对管道的压力等于小球的重力,选项A错误;
C.小球从出发点到管道最低点,由动能定理可得mgR=mv22-mv02,解得小球到达管道最低点时速度v2=m/s,在最低点,由牛顿第二定律F-mg=,解得管道最低点对小球的支持力F=5N,再结合牛顿第三定律可知,选项C错误;
D.小球刚好通过圆轨道最高点,在最高点速度v满足mg=,解得v=,小球从出发点到圆轨道最高点由动能定理可得:mgR-2mgr=mv2-mv02,联立得:r=4m,故D正确。
(2022.广东.检测)如图甲所示,陀螺可在圆轨道外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”。它可等效为一质点在圆轨道外侧运动的模型,如图乙所示。在竖直平面内固定的强磁性圆轨道半径为R,A、B两点分别为轨道的最高点与最低点。质点沿轨道外侧做完整的圆周运动,所受圆轨道的强磁性引力始终指向圆心O且大小恒为F,当质点以速率v=通过A点时,对轨道的压力为其重力的8倍,不计摩擦和空气阻力,质点质量为m,重力加速度为g,则( )
A.强磁性引力的大小F=7mg
B.质点在A点对轨道的压力小于在B点对轨道的压力
C.只要质点能做完整的圆周运动,则质点对A、B两点的压力差恒为5mg
D.若强磁性引力大小恒为2F,为确保质点做完整的圆周运动,则质点通过B点的最大速率为
A、质点在A点,由牛顿第二定律有:F+mg-FA=,根据牛顿第三定律有:FA=FA′=8mg,联立解得:F=8mg,选项A错误;
BC、质点能完成圆周运动,则在A点根据牛顿第二定律有:F+mg-NA=,根据牛顿第三定律有:NA=NA′;在B点,根据牛顿第二定律有:F-mg-NB=,根据牛顿第三定律有:NB=NB′;从A点到B点过程,根据动能定理有:mg 2R=-。
联立解得:NA′-NB′=6mg,选项BC错误;
D、若强磁性引力大小恒为2F,在B点根据牛顿第二定律有2F-mg-FB=,当FB=0时,质点速度最大,联立解得vB′=,故选D。
解决竖直平面内的圆周运动临界问题的解题思路:
斜面上的圆周运动及临界问题
(2022.河北.月考)如图所示,一倾斜的匀质圆盘可绕垂直于盘面的固定中心轴转动,盘面上离转轴距离为l=6.25cm处有一质量为m=0.4kg的小物体(可视为质点)静止在倾斜的匀质圆盘上,物体与盘面间的动摩擦因数为μ=,盘面与水平面的夹角为θ=30°。设最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2。
(1)若小物体与圆盘始终保持相对静止,求圆盘匀速转动角速度的最大值;(计算结果保留根式)
(2)若小物体与圆盘始终保持相对静止,当圆盘匀速转动的角速度达最大值时,求小物体运动到最高点时所受摩擦力;
(3)若小物块在最高点不受摩擦力,求此时小物块的角速度和线速度大小。(计算结果保留根式)
关键信息:小物体随圆盘一起做匀速转动 → 斜面模型+匀速圆周运动;
小物体在圆盘最低点 → 所受摩擦力最大,临界点1:角速度最大;
小物体在圆盘最高点 → 所受摩擦力为零,临界点2:只有重力沿斜面向下的分力提供向心力。
解题思路:“两点”即最高点和最低点,在最高点和最低点对小球受力分析,找出向心力的来源,根据牛顿第二定律列方程求解。
(1)小物块在最低点相对圆盘即将滑动时,圆盘匀速转动角速度最大,受力分析如图所示:
f1=μmgcos30°
由牛顿第二定律有μmgcos30°-mgsin30°=,
代入数据解得ω1=rad/s;
(2)设小物体在最高点所受摩擦力大小为f,方向沿斜面向上,受力分析如图所示:
根据牛顿第二定律得mgsin30°-f=,
代入数据解得f=1N,方向沿圆盘面向上;
(3)小物块在最高点不受摩擦力,根据牛顿第二定律有
mgsin30°=,
解得小物块在最高点不受摩擦力时的角速度ω2=,
代入数据解得ω2=rad/s,
小物块在最高点不受摩擦力时的线速度大小v=ω2l=m/s
(2021.江苏.检测)如图所示,两个质量均为m的小物块a和b(可视为质点),静止在倾斜的匀质圆盘上,圆盘可绕垂直于盘面的固定轴转动,a到转轴的距离为l,b到转轴的距离为2l,物块与盘面间的动摩擦因数为,盘面与水平面的夹角为30°。设最大静摩擦力等于滑动摩擦力,重力加速度大小为g,若a、b随圆盘以角速度ω匀速转动,下列说法正确的是( )
A.a在最高点时所受摩擦力可能为0 B.a在最低点时所受摩擦力可能为0
C.ω=是a开始滑动的临界角速度 D.ω=是b开始滑动的临界角速度
A.假设在最高点,若a所受的摩擦力为零,仅靠重力沿圆盘向下的分力提供向心力,有:mgsinθ=mlω2,在最低点,有f-mgsinθ=mlω2,解得最低点的摩擦力f=mg,而最大静摩擦力fm=μmgcosθ=0.75mg,可知最高点a的摩擦力不会为零,选项A错误;
B.在最低点,a靠静摩擦力和重力沿圆盘方向的分力提供向心力,合力指向圆心,则静摩擦力大于重力沿圆盘方向的分力,选项B错误;
C.在最低点,对a,根据牛顿第二定律得,μmgcos30°-mgsin30°=mlω2,解得a开始滑动的临界角速度ω=,选项C错误;
D.在最低点,对b,根据牛顿第二定律得,μmgcos30°-mgsin30°=m 2lω'2,解得b开始滑动的临界角速度ω'=,选项D正确;
故选D。
求解斜面上圆周运动问题的“三个关键”:
(1)物体在垂直于斜面方向上的合力一定为零;
(2)物体在斜面内指向圆心方向的合力提供向心力;
(3)物体经过斜面上最高点、最低点时的临界条件。
斜面上的圆周运动要根据具体情境,可以借助于处理竖直面内的圆周运动模型的方法分析解决。
水平面内圆周运动及临界问题
(2021.湖北.检测)水平圆盘上沿直径方向放置以轻绳相连的两个小物块A和B,两物块的质量分别为mA和mB,到圆心的距离分别为rA和rB,且rA<rB。两物块与圆盘间的最大静摩擦力均为自身重力的μ倍,重力加速度为g。忽略小物块A、B的大小,不考虑轻绳拉力上限,轻绳伸直且最初拉力为零。圆盘绕过圆心的竖直轴转动,转动的角速度ω由零缓慢增大。
(1)当圆盘以角速度ω1匀速转动时,轻绳上开始出现拉力,求ω1的大小;
(2)当圆盘以角速度ω2匀速转动时,小物块A将开始滑动,求ω2的大小;
(3)在角速度从零缓慢地增加到小物块A将开始滑动过程中,小物块A与圆盘间摩擦力大小为fA,试通过计算,在坐标系中作出fA-ω2图象(要求:必须标出每段图象转折点的纵坐标值)。
关键信息:、随圆盘一起绕过圆心的竖直轴转动 → 水平圆盘模型
A、B随圆盘一起绕过圆心的竖直轴转动 → 水平圆盘模型
rA<rB,且圆盘转速逐渐增大 → 物块滑动的临界状态为,则,,故wB临<wA临,即B比A先达到临界状态。
解题思路:抓住A刚要滑动和B刚要滑动时的两个临界状态,B所受的静摩擦力刚好达最大值时,细绳刚开始有拉力;A所受的静摩擦力刚好到达最大值时,A、B刚好同时相对圆盘发生滑动。
(1)当角速度较小时,轻绳张力T=0,
圆盘对A、B的静摩擦力提供其绕轴做圆周运动的向心力,即f0=mω2r。
当圆盘转速增大时,因为rA<rB,所以物体B先达到最大静摩擦力,
对B:μmBg=mBω12rB,即当ω1=时,轻绳上开始出现拉力。
(2)当ω>ω1时,轻绳开始出现张力,
对A:fA-T=mA ω2 rA ①
对B:μmBg+T=mBω2rB ②
由①+②得fA+μmBg=(mArA+mBrB)ω2,则当角速度ω增大时,fA一直增大,当A将要开始滑动时fA=μmAg,解得ω2=。
(3)由第(1)问可得,当0<ω≤ω1时,fA=mArAω2,令ω=ω1时,解得fA=
由第(2)问可得,当ω1<ω≤ω2时,
fA=(mArA+mBrB)ω2-μmBg,
令ω=ω2时,解得fA=μmAg
综上作出fA-ω2图象如图所示
(2022.重庆.检测)如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合。转台以一定角速度匀速转动,一质量为m的小物块(可视为质点)落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,小物块与陶罐内壁间的动摩擦因数为μ,且它和O点的连线与OO′之间的夹角为θ,转动角速度为ω,重力加速度为g。则下列说法正确的是( )
A.当ω2=时,小物块与陶罐内壁间的弹力为mgcosθ
B.当ω2=时,小物块与陶罐内壁间的弹力为
C.当ω2=时,小物块与陶罐内壁间的摩擦力沿罐壁向上
D.当ω2=时,小物块将向陶罐上沿滑动
ABC、当摩擦力恰好为零,受力分析如图所示,支持力和重力的合力提供向心力,设此时角速度为ω0,有:mgtanθ=mRsinθω02,
解得ω02=,此时小物块与陶罐内壁间的弹力为N=,故AC错误,B正确;
D、当角速度最大时,摩擦力方向沿罐壁切线向下达最大值,超过最大值物块将向陶罐上沿滑动,受力分析图如下:
设此最大角速度为ω,
水平方向:fcosθ+Nsinθ=mRsinθω2,
竖直方向:fsinθ+mg=Ncosθ,其中f=μN,
联立解得ω2=,D错误,故选B。
水平面内圆周运动常见的三种临界情况分析:
临界情况 典型模型 临界条件分析
相对滑动的临界条件 两物体相对静止且存在着摩擦力时,二者相对滑动的临界条件是静摩擦力刚好达到最大值
接触与分离的临界条件 两物体恰好接触或分离,临界条件是弹力Fn=0
绳子断裂与松弛的临界条件 绳子所能承受的张力是有限度的,绳子恰不断裂的临界条件是绳中张力等于它所能承受的最大张力,绳子松弛的临界条件是绳子张力为0
竖直面内圆周运动及临界问题
(2022.海南.检测) 如图所示,一质量为m=0.1kg的小球以竖直向上的初速度v0=10m/s冲入一管道。该管道为圆管道,半径为R=5m。已知小球的入口与圆心在同一高度。经过管道后,它又沿着水平导轨进入另一半径为r的圆轨道,且恰好能通过圆轨道的最高点,若所有衔接处均不损失机械能,不计摩擦,小球直径以及管道内径可忽略,圆轨道和圆轨道底端均与水平导轨相切,g取10 m/s2。下列说法正确的是( )
A.小球到达管道最高点时对管道的压力为零
B.小球到达管道最高点时速度为m/s
C.小球到达管道最低点时对管道的压力为6N
D.圆轨道半径r为4m
关键信息:光滑圆管道 → 轻杆模型,最高点速度v≥0
光滑圆轨道 → 轻绳模型,恰好能通过最高点的临界v=
解题思路:“两点”即最高点和最低点,在最高点和最低点对小球受力分析,找出向心力的来源,根据牛顿第二定律列方程,“一过程”,即从最高点到最低点(或从最低点到最高点),用动能定理或机械能守恒定律将这两点联系起来。
B.小球从出发点到管道最高点,由动能定理可得-mgR=mv12-mv02,解得小球到达管道最高的点时速度v1=0,选项B错误;
A.小球在最高点时,小球对管道的压力等于小球的重力,选项A错误;
C.小球从出发点到管道最低点,由动能定理可得mgR=mv22-mv02,解得小球到达管道最低点时速度v2=m/s,在最低点,由牛顿第二定律F-mg=,解得管道最低点对小球的支持力F=5N,再结合牛顿第三定律可知,选项C错误;
D.小球刚好通过圆轨道最高点,在最高点速度v满足mg=,解得v=,小球从出发点到圆轨道最高点由动能定理可得:mgR-2mgr=mv2-mv02,联立得:r=4m,故D正确。
(2022.广东.检测)如图甲所示,陀螺可在圆轨道外侧旋转而不脱落,好像轨道对它施加了魔法一样,被称为“魔力陀螺”。它可等效为一质点在圆轨道外侧运动的模型,如图乙所示。在竖直平面内固定的强磁性圆轨道半径为R,A、B两点分别为轨道的最高点与最低点。质点沿轨道外侧做完整的圆周运动,所受圆轨道的强磁性引力始终指向圆心O且大小恒为F,当质点以速率v=通过A点时,对轨道的压力为其重力的8倍,不计摩擦和空气阻力,质点质量为m,重力加速度为g,则( )
A.强磁性引力的大小F=7mg
B.质点在A点对轨道的压力小于在B点对轨道的压力
C.只要质点能做完整的圆周运动,则质点对A、B两点的压力差恒为5mg
D.若强磁性引力大小恒为2F,为确保质点做完整的圆周运动,则质点通过B点的最大速率为
A、质点在A点,由牛顿第二定律有:F+mg-FA=,根据牛顿第三定律有:FA=FA′=8mg,联立解得:F=8mg,选项A错误;
BC、质点能完成圆周运动,则在A点根据牛顿第二定律有:F+mg-NA=,根据牛顿第三定律有:NA=NA′;在B点,根据牛顿第二定律有:F-mg-NB=,根据牛顿第三定律有:NB=NB′;从A点到B点过程,根据动能定理有:mg 2R=-。
联立解得:NA′-NB′=6mg,选项BC错误;
D、若强磁性引力大小恒为2F,在B点根据牛顿第二定律有2F-mg-FB=,当FB=0时,质点速度最大,联立解得vB′=,故选D。
解决竖直平面内的圆周运动临界问题的解题思路:
斜面上的圆周运动及临界问题
(2022.河北.月考)如图所示,一倾斜的匀质圆盘可绕垂直于盘面的固定中心轴转动,盘面上离转轴距离为l=6.25cm处有一质量为m=0.4kg的小物体(可视为质点)静止在倾斜的匀质圆盘上,物体与盘面间的动摩擦因数为μ=,盘面与水平面的夹角为θ=30°。设最大静摩擦力等于滑动摩擦力,重力加速度g取10m/s2。
(1)若小物体与圆盘始终保持相对静止,求圆盘匀速转动角速度的最大值;(计算结果保留根式)
(2)若小物体与圆盘始终保持相对静止,当圆盘匀速转动的角速度达最大值时,求小物体运动到最高点时所受摩擦力;
(3)若小物块在最高点不受摩擦力,求此时小物块的角速度和线速度大小。(计算结果保留根式)
关键信息:小物体随圆盘一起做匀速转动 → 斜面模型+匀速圆周运动;
小物体在圆盘最低点 → 所受摩擦力最大,临界点1:角速度最大;
小物体在圆盘最高点 → 所受摩擦力为零,临界点2:只有重力沿斜面向下的分力提供向心力。
解题思路:“两点”即最高点和最低点,在最高点和最低点对小球受力分析,找出向心力的来源,根据牛顿第二定律列方程求解。
(1)小物块在最低点相对圆盘即将滑动时,圆盘匀速转动角速度最大,受力分析如图所示:
f1=μmgcos30°
由牛顿第二定律有μmgcos30°-mgsin30°=,
代入数据解得ω1=rad/s;
(2)设小物体在最高点所受摩擦力大小为f,方向沿斜面向上,受力分析如图所示:
根据牛顿第二定律得mgsin30°-f=,
代入数据解得f=1N,方向沿圆盘面向上;
(3)小物块在最高点不受摩擦力,根据牛顿第二定律有
mgsin30°=,
解得小物块在最高点不受摩擦力时的角速度ω2=,
代入数据解得ω2=rad/s,
小物块在最高点不受摩擦力时的线速度大小v=ω2l=m/s
(2021.江苏.检测)如图所示,两个质量均为m的小物块a和b(可视为质点),静止在倾斜的匀质圆盘上,圆盘可绕垂直于盘面的固定轴转动,a到转轴的距离为l,b到转轴的距离为2l,物块与盘面间的动摩擦因数为,盘面与水平面的夹角为30°。设最大静摩擦力等于滑动摩擦力,重力加速度大小为g,若a、b随圆盘以角速度ω匀速转动,下列说法正确的是( )
A.a在最高点时所受摩擦力可能为0 B.a在最低点时所受摩擦力可能为0
C.ω=是a开始滑动的临界角速度 D.ω=是b开始滑动的临界角速度
A.假设在最高点,若a所受的摩擦力为零,仅靠重力沿圆盘向下的分力提供向心力,有:mgsinθ=mlω2,在最低点,有f-mgsinθ=mlω2,解得最低点的摩擦力f=mg,而最大静摩擦力fm=μmgcosθ=0.75mg,可知最高点a的摩擦力不会为零,选项A错误;
B.在最低点,a靠静摩擦力和重力沿圆盘方向的分力提供向心力,合力指向圆心,则静摩擦力大于重力沿圆盘方向的分力,选项B错误;
C.在最低点,对a,根据牛顿第二定律得,μmgcos30°-mgsin30°=mlω2,解得a开始滑动的临界角速度ω=,选项C错误;
D.在最低点,对b,根据牛顿第二定律得,μmgcos30°-mgsin30°=m 2lω'2,解得b开始滑动的临界角速度ω'=,选项D正确;
故选D。
求解斜面上圆周运动问题的“三个关键”:
(1)物体在垂直于斜面方向上的合力一定为零;
(2)物体在斜面内指向圆心方向的合力提供向心力;
(3)物体经过斜面上最高点、最低点时的临界条件。
斜面上的圆周运动要根据具体情境,可以借助于处理竖直面内的圆周运动模型的方法分析解决。
同课章节目录
