电场与磁场——电场的基本性质(学案)-2023年新高考物理二轮复习专题讲义
文档属性
| 名称 | 电场与磁场——电场的基本性质(学案)-2023年新高考物理二轮复习专题讲义 |  | |
| 格式 | docx | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-31 22:02:09 | ||
图片预览




文档简介
电场的基本性质
电场的力的性质
(2021年湖南卷)如图,在(a,0)位置放置电荷量为q的正点电荷,在(0,a)位置放置电荷量为q的负点电荷,在距P(a,a)为a的某点处放置正点电荷Q,使得P点的电场强度为零。则Q的位置及电荷量分别为( )
A.(0,2a), B.(0,2a),
C.(2a,0), D.(2a,0),
关键信息:点电荷 → 点电荷的场强
P点的电场强度为零 → 场强叠加原理(平行四边形定则)
在距P(a,a)为的某点处放置正点电荷Q → 点电荷Q位于以P(a,a)为圆心为半径的圆周上,确定了点电荷Q产生的场强的方向,即可确定点电荷Q具体位置
解题思路:根据点电荷场强的决定式确定场强,利用平行四边形定则进行矢量叠加
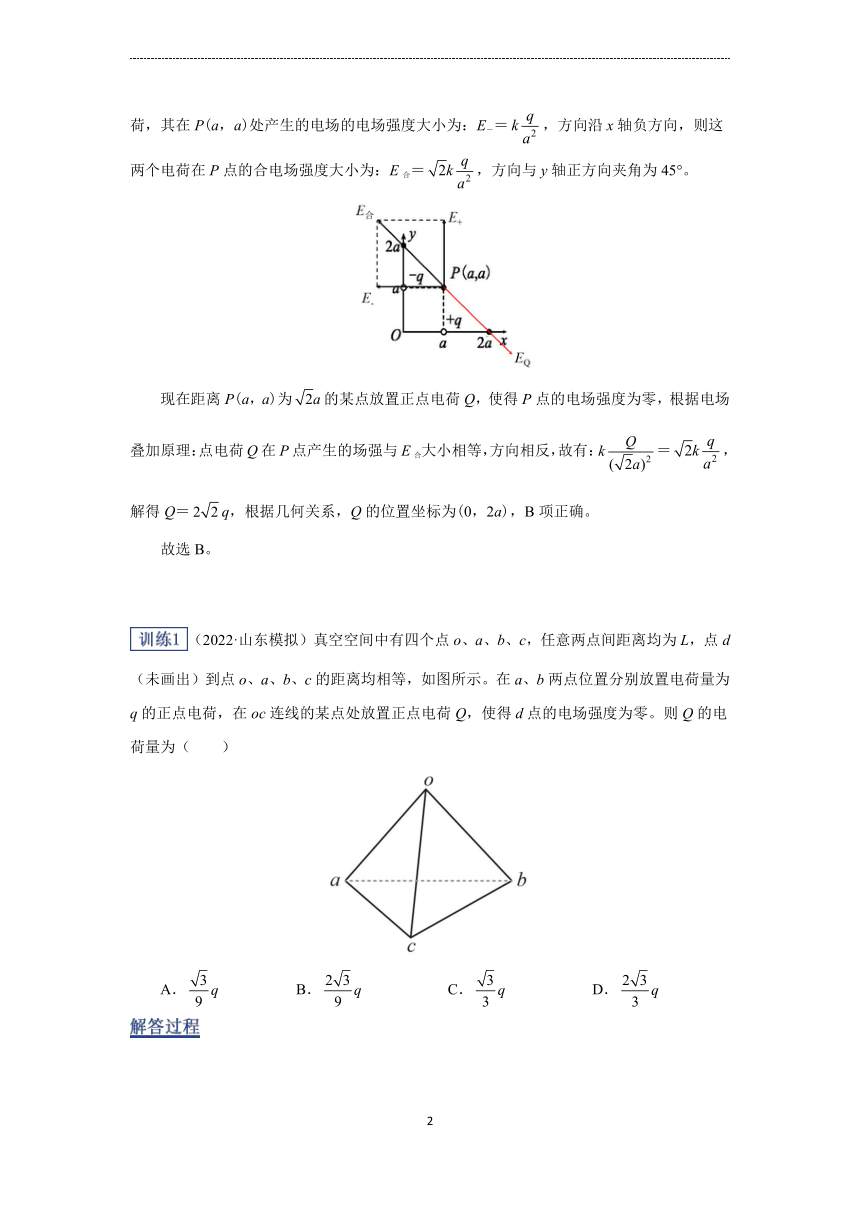
如图所示:在(a,0)位置放置电荷量为q的正点电荷,其在P(a,a)处产生的电场的电场强度大小为:E+=,方向沿y轴正方向,在(0,a)位置放置的电荷量为q的负点电荷,其在P(a,a)处产生的电场的电场强度大小为:E-=,方向沿x轴负方向,则这两个电荷在P点的合电场强度大小为:E合=,方向与y轴正方向夹角为45°。
现在距离P(a,a)为的某点放置正点电荷Q,使得P点的电场强度为零,根据电场叠加原理:点电荷Q在P点产生的场强与E合大小相等,方向相反,故有:=,解得Q=q,根据几何关系,Q的位置坐标为(0,2a),B项正确。
故选B。
(2022·山东模拟)真空空间中有四个点o、a、b、c,任意两点间距离均为L,点d(未画出)到点o、a、b、c的距离均相等,如图所示。在a、b两点位置分别放置电荷量为q的正点电荷,在oc连线的某点处放置正点电荷Q,使得d点的电场强度为零。则Q的电荷量为( )
A. B. C. D.
根据题意可知o、a、b、c构成正四面体,由于d与各点等距,所以d位于正四面体的中心,根据几何关系可得:
在a、b两点位置分别放置电荷量为q的正点电荷,由对称性以及矢量叠加原理分析可得,这两个点电荷在d点所产生的合场强方向垂直与oc,指向oc的中点e,根据几何关系可得:,故要使d点的电场强度为零,则正点电荷Q应当放置于e点,正点电荷Q在d点所产生的场强为:。结合几何关系,a、b处电荷量为q的正点电荷在d点产生的合场强大小为:,因e点合场强为0,得:
解得:,B正确,ACD错误。
故选B。
电场强度的计算方法
(1)定义式法:
(2)点电荷电场强度公式法:直接用点电荷的电场强度公式求解。若要求多个点电荷产生电场的合电场强度,则可先分别求出各个点电荷产生的电场强度,然后利用矢量叠加法求出合电场强度。
(3)根据匀强电场场强和电势差的关系式:求解
(4)物理思想方法:对于较复杂的求电场强度的问题可用物理思想方法分析解决。如:“微元法”“对称性分析法”“补偿法”等。
电场的能的性质
(智学精选)如图所示,虚线A、B、C、D是某匀强电场中的四条平行且等距的等势面,两相邻等势面间的距离为2cm,其中等势面C的电势为0,一电子仅在静电力的作用下运动,经过A、D等势面时的动能分别为28eV和10eV,则下列说法正确的是( )
A.等势面D的电势为6V
B.该匀强电场的电场强度为3V/m,方向水平向右
C.该电子不可能到达电势为-12V的等势面
D.该电子运动到某一位置,其电势能变为8eV时,它的动能为8eV
关键信息:匀强电场,平行且等距的等势面 → 等差等势面
等势面C的电势为0 → 电子在该等势面电势能为0
仅在静电力的作用下运动 → 电势能和动能之和为定值
解题思路:匀强电场中平行且等距的等势面为等差等势面,即相邻等势面电势差相等,电场线与等势面垂直且方向由高电势指向低电势,场强可通过进行计算;带电粒子仅在电场力作用下运动时动能和电势能之和为定值,动能与电势能相互转化。
A.根据动能定理,-eUAD=EkD-EkA,解得AD间的电势差UAD=18V,因为是四条平行且等距的等势面,故相邻等势面之间的电势差为6V,又因为等势面C的电势为0,所以φA=12V ,φB=6V,φD=-6V ,故A错误;
B.根据可得E=300 V/m,因为沿电场线方向电势降低,所以场强方向水平向右,故B错误;
C.由题意可知电子每经过相邻等势面,损失的动能为6 eV,所以该电子仍可以到达电势为-12V的等势面,根据动能定理可知,还有4eV的动能,故C错误;
D.在只有电场力做功的条件下动能和电势能的总和保持不变,C点电势能为0 eV,动能为16 eV,所以该电子的电势能与动能之和为16 eV,所以该电子运动到某一位置,其电势能变为8 eV时,它的动能为8 eV,故D正确。
故选D。
(智学精选)如图所示,实线为某一带电粒子在某点电荷电场中的运动轨迹,轨迹关于虚线PQ对称,轨迹与PQ相交于A点,轨迹上M、N两点关于PQ对称,粒子只受电场力作用,则下列说法正确的是( )
A.点电荷一定在PQ上且处于轨迹内侧 B.带电粒子在M、N两点受力相同
C.M、N两点电势一定相同 D.带电粒子在A点的动能一定最大
带电粒子在点电荷电场中只受电场力作用,其运动轨迹具有对称性,且对称轴一定是过点电荷的直线,所以点电荷一定在PQ上,如果带电粒子与点电荷带同种电荷,根据受力情况,点电荷处于轨迹的外侧,如果是异种电荷,点电荷处于轨迹内侧,A错误;
B.带电粒子在M、N两点受力大小相等,但是方向不相同,B错误;
C.根据对称性,M、N两点到点电荷的距离相同,一定在同一等势面上,电势一定相同,C正确;
D.根据轨迹可以判断,带电粒子所受到的静电力方向指向轨迹内侧,所以带电粒子在经过A点前后的过程中,静电力先做负功再做正功,动能先减小再增大,所以D错误。
故选C。
分析电场中带电粒子运动轨迹类问题,要把握以下两点:
(1)“运动与力两线法”——画出“速度线”(运动轨迹在初始位置的切线)与“力线”(在初始位置电场线的切线方向),从二者的夹角情况来分析曲线运动的情况。
(2)“三不知时要假设”——电荷的正负、电场强度的方向(或等势面电势的高低)、电荷运动的方向,是题意中相互制约的三个方面。若已知其中的任一个,可顺次向下分析判定各待求量;若三个都不知(三不知),则要用“假设法”分别讨论各种情况。
电容器
(2021年淮南二模)如图所示,在水平放置的两平行金属板M、N之间的P点,有一个带电荷量为-q的点电荷恰好静止,两金属板通过电阻R接到恒压直流电源上,其中N板接地。保持其他条件不变,仅移动金属板M,下列判断正确的是( )
A.仅将M板向上移动一小段距离,P点的电势升高
B.仅将M板向下移动一小段距离,金属板M带电荷量减少
C.仅将M板向右移动一小段距离,该点电荷仍将保持静止
D.仅将M板向左移动一小段距离,该点电荷在P点的电势能变小
关键信息:两金属板接到恒压直流电源上 → 极板间电压U恒定
仅将M板上下移动 → 只改变极板间距离d
仅将M板左右移动 → 只改变极板正对面积S
解题思路:U恒定,d与S变化引起C变化,继而引起Q、E变化及P点的电势变化
根据电容的定义式、平行板电容器电容的决定式、匀强电场场强与电势差的关系式、电势的定义式进行综合判断
A.电容器和电源相连,电容器两端的电压不变,根据公式E=可知,将M板向上移动一小段距离,d增大,E减小,P点和N板间的电势差,不变,故P点和N板间的电势差减小,而N板的电势不变,故P点的电势降低,A项错误。
B.根据公式C=,将M板向下移动一小段距离,d减小,C变大。根据公式Q=CU可知,金属板M带电荷量增加,B项错误。
C.根据公式E=知,将M板向右移动一小段距离,d不变,E不变,所以该点电荷仍将保持静止,C项正确。
D.根据公式E=知,将M板向左移动一小段距离,d不变,E不变,所以P点和N板间的电势差不变,而N板的电势不变,故P点的电势不变,该点电荷在P点的电势能不变,D项错误。
故选C。
(智学精选)如图所示,一平行板电容器充电后与电源断开,负极板接地,两板间的P点固定一个带正电的检验电荷。用C表示电容器的电容,E表示两板间的电场强度的大小,φ表示P点的电势,Ep表示正电荷在P点的电势能。若正极板保持不动,将负极板缓慢向左平移一小段距离l0,上述各物理量与负极板移动距离x(x≤l0)的关系图像中正确的是( )
A. B.
C. D.
A、当负极板左移时,两板间的距离增加,由C=可知,C与x的图像不是一次函数图像,故A错误;
B、由U=可知:U=Q,则电场强度E==,E与d、x无关,故B错误;
C、因负极板接地,设P点开始距负极板的距离是d′,则P点的电势:φ=E(d′+x),故C正确;
D、正电荷在P点的电势能:Ep=qφ=qE(d′+x)=qEd′+qEx,所以Ep-x图像是一条倾斜的直线,故D错误。
故选:C。
电容器动态变化两类典型问题:
1.电容器始终与恒压电源相连,电容器两极板间的电势差U保持不变。
(1)根据先分析电容的变化,再由C=分析Q的变化。
(2)根据E=分析场强的变化。
(3)根据UAB=E·d=φA-φB分析某点电势变化。
2.电容器充电后与电源断开,电容器两极板所带的电荷量Q保持不变。
(1)根据先分析电容的变化,再由C=分析U的变化。
(2)根据分析场强变化。
电场中的图像问题
(智学精选)空间中存在一静电场,一电子仅在电场力作用下沿x轴正方向运动,其电势能随位置x的变化关系如图所示,则电子从x1向x3运动的过程中,下列说法正确的是( )
A.在x1处电子速度最大 B.在x2处电子加速度最大
C.在x3处电场强度最大 D.在x2处电势最高
关键信息:仅在电场力作用下 → ①只有电场力做功,电势能与动能相互转化,总量不变②电场力沿x轴方向,图线切线斜率表示该处电场力的大小
解题思路:根据可知,Ep-x图像的斜率绝对值代表静电力的大小,同时结合电场中的功能关系判断电子的动能、速度以及加速度的特征。
A.电子仅在电场力作用下运动,动能与电势能之和是恒定的,则电子从x1向x3运动的过程中,在x3处的电势能最小,则动能最大,速度最大,A错误;
B.根据可知,图象的斜率绝对值表示电子受到的电场力大小,在x2处图象的斜率为0,则电场力为0,故电子的加速度为0,B错误;
C.电子从x1向x3运动的过程中,x3处的图象斜率绝对值最大,则电场力最大,根据F=Eq可知,x3处的电场强度最大,C正确;
D.电子从x1向x3运动的过程中,电子在x2处电势能最大,但由于电子带负电,根据可知,x2处电势最低,D错误;
故选C。
(智学精选)两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两点电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势为零,ND段中C点电势最高,则( )
A.A点的电场强度大小为零
B.q1和q2带异种电荷,且q1的带电量大于q2的带电量
C.CD间的场强方向沿x轴负方向
D.将一负电荷沿x轴从N点移到D点,电势能先增大后减小
A.因为φ x图像的斜率的绝对值等于电场强度E的大小,根据图像可知,A点斜率不为零,场强不为零,故A错误;
B.由于沿着电场线方向电势降低,且A点电势为零,所以O点的电荷q1带正电,M点电荷q2带负电;由于C点合场强为零,根据公式可知,q1距离远,电荷量大,所以q1电荷量大于q2的电荷量,故B正确;
C.由图像可知从C到D电势逐渐降低,故CD间的场强方向沿x轴正方向,故C错误;
D.因为沿x轴从N点移到D点,电势先升高后降低,根据可知,负电荷从N点移到D点电势能先减小后增大,故D错误。
故选B。
电场中图像类问题的分析方法:
1.明确图像中的横轴与纵轴所代表的物理量,要区分图像中相关物理量的正负值的物理意义,要注意分析各段不同函数形式的图线所表征的物理过程;
2.要明确有关图线所包围的面积、斜率、截距所表示的物理意义,根据图像所描绘的物理过程,运用相应的物理规律计算求解;
3.同时解决此类问题要牢牢记住并理解几种常见图像的特点。
(1)φ-x图像中电场强度的大小等于φ-x图线的斜率大小,电场强度为零处,φ-x图线存在极值,其切线的斜率为零;
(2)E-x图像中图线与x轴围成的“面积”表示电势差,“面积”大小表示电势差大小,两点的电势高低根据电场方向判定;
(3)Ep-x图像中,只要粒子只受电场力作用,则,即Ep-x图像的斜率大小即为粒子所受电场力大小。
2
电场的力的性质
(2021年湖南卷)如图,在(a,0)位置放置电荷量为q的正点电荷,在(0,a)位置放置电荷量为q的负点电荷,在距P(a,a)为a的某点处放置正点电荷Q,使得P点的电场强度为零。则Q的位置及电荷量分别为( )
A.(0,2a), B.(0,2a),
C.(2a,0), D.(2a,0),
关键信息:点电荷 → 点电荷的场强
P点的电场强度为零 → 场强叠加原理(平行四边形定则)
在距P(a,a)为的某点处放置正点电荷Q → 点电荷Q位于以P(a,a)为圆心为半径的圆周上,确定了点电荷Q产生的场强的方向,即可确定点电荷Q具体位置
解题思路:根据点电荷场强的决定式确定场强,利用平行四边形定则进行矢量叠加
如图所示:在(a,0)位置放置电荷量为q的正点电荷,其在P(a,a)处产生的电场的电场强度大小为:E+=,方向沿y轴正方向,在(0,a)位置放置的电荷量为q的负点电荷,其在P(a,a)处产生的电场的电场强度大小为:E-=,方向沿x轴负方向,则这两个电荷在P点的合电场强度大小为:E合=,方向与y轴正方向夹角为45°。
现在距离P(a,a)为的某点放置正点电荷Q,使得P点的电场强度为零,根据电场叠加原理:点电荷Q在P点产生的场强与E合大小相等,方向相反,故有:=,解得Q=q,根据几何关系,Q的位置坐标为(0,2a),B项正确。
故选B。
(2022·山东模拟)真空空间中有四个点o、a、b、c,任意两点间距离均为L,点d(未画出)到点o、a、b、c的距离均相等,如图所示。在a、b两点位置分别放置电荷量为q的正点电荷,在oc连线的某点处放置正点电荷Q,使得d点的电场强度为零。则Q的电荷量为( )
A. B. C. D.
根据题意可知o、a、b、c构成正四面体,由于d与各点等距,所以d位于正四面体的中心,根据几何关系可得:
在a、b两点位置分别放置电荷量为q的正点电荷,由对称性以及矢量叠加原理分析可得,这两个点电荷在d点所产生的合场强方向垂直与oc,指向oc的中点e,根据几何关系可得:,故要使d点的电场强度为零,则正点电荷Q应当放置于e点,正点电荷Q在d点所产生的场强为:。结合几何关系,a、b处电荷量为q的正点电荷在d点产生的合场强大小为:,因e点合场强为0,得:
解得:,B正确,ACD错误。
故选B。
电场强度的计算方法
(1)定义式法:
(2)点电荷电场强度公式法:直接用点电荷的电场强度公式求解。若要求多个点电荷产生电场的合电场强度,则可先分别求出各个点电荷产生的电场强度,然后利用矢量叠加法求出合电场强度。
(3)根据匀强电场场强和电势差的关系式:求解
(4)物理思想方法:对于较复杂的求电场强度的问题可用物理思想方法分析解决。如:“微元法”“对称性分析法”“补偿法”等。
电场的能的性质
(智学精选)如图所示,虚线A、B、C、D是某匀强电场中的四条平行且等距的等势面,两相邻等势面间的距离为2cm,其中等势面C的电势为0,一电子仅在静电力的作用下运动,经过A、D等势面时的动能分别为28eV和10eV,则下列说法正确的是( )
A.等势面D的电势为6V
B.该匀强电场的电场强度为3V/m,方向水平向右
C.该电子不可能到达电势为-12V的等势面
D.该电子运动到某一位置,其电势能变为8eV时,它的动能为8eV
关键信息:匀强电场,平行且等距的等势面 → 等差等势面
等势面C的电势为0 → 电子在该等势面电势能为0
仅在静电力的作用下运动 → 电势能和动能之和为定值
解题思路:匀强电场中平行且等距的等势面为等差等势面,即相邻等势面电势差相等,电场线与等势面垂直且方向由高电势指向低电势,场强可通过进行计算;带电粒子仅在电场力作用下运动时动能和电势能之和为定值,动能与电势能相互转化。
A.根据动能定理,-eUAD=EkD-EkA,解得AD间的电势差UAD=18V,因为是四条平行且等距的等势面,故相邻等势面之间的电势差为6V,又因为等势面C的电势为0,所以φA=12V ,φB=6V,φD=-6V ,故A错误;
B.根据可得E=300 V/m,因为沿电场线方向电势降低,所以场强方向水平向右,故B错误;
C.由题意可知电子每经过相邻等势面,损失的动能为6 eV,所以该电子仍可以到达电势为-12V的等势面,根据动能定理可知,还有4eV的动能,故C错误;
D.在只有电场力做功的条件下动能和电势能的总和保持不变,C点电势能为0 eV,动能为16 eV,所以该电子的电势能与动能之和为16 eV,所以该电子运动到某一位置,其电势能变为8 eV时,它的动能为8 eV,故D正确。
故选D。
(智学精选)如图所示,实线为某一带电粒子在某点电荷电场中的运动轨迹,轨迹关于虚线PQ对称,轨迹与PQ相交于A点,轨迹上M、N两点关于PQ对称,粒子只受电场力作用,则下列说法正确的是( )
A.点电荷一定在PQ上且处于轨迹内侧 B.带电粒子在M、N两点受力相同
C.M、N两点电势一定相同 D.带电粒子在A点的动能一定最大
带电粒子在点电荷电场中只受电场力作用,其运动轨迹具有对称性,且对称轴一定是过点电荷的直线,所以点电荷一定在PQ上,如果带电粒子与点电荷带同种电荷,根据受力情况,点电荷处于轨迹的外侧,如果是异种电荷,点电荷处于轨迹内侧,A错误;
B.带电粒子在M、N两点受力大小相等,但是方向不相同,B错误;
C.根据对称性,M、N两点到点电荷的距离相同,一定在同一等势面上,电势一定相同,C正确;
D.根据轨迹可以判断,带电粒子所受到的静电力方向指向轨迹内侧,所以带电粒子在经过A点前后的过程中,静电力先做负功再做正功,动能先减小再增大,所以D错误。
故选C。
分析电场中带电粒子运动轨迹类问题,要把握以下两点:
(1)“运动与力两线法”——画出“速度线”(运动轨迹在初始位置的切线)与“力线”(在初始位置电场线的切线方向),从二者的夹角情况来分析曲线运动的情况。
(2)“三不知时要假设”——电荷的正负、电场强度的方向(或等势面电势的高低)、电荷运动的方向,是题意中相互制约的三个方面。若已知其中的任一个,可顺次向下分析判定各待求量;若三个都不知(三不知),则要用“假设法”分别讨论各种情况。
电容器
(2021年淮南二模)如图所示,在水平放置的两平行金属板M、N之间的P点,有一个带电荷量为-q的点电荷恰好静止,两金属板通过电阻R接到恒压直流电源上,其中N板接地。保持其他条件不变,仅移动金属板M,下列判断正确的是( )
A.仅将M板向上移动一小段距离,P点的电势升高
B.仅将M板向下移动一小段距离,金属板M带电荷量减少
C.仅将M板向右移动一小段距离,该点电荷仍将保持静止
D.仅将M板向左移动一小段距离,该点电荷在P点的电势能变小
关键信息:两金属板接到恒压直流电源上 → 极板间电压U恒定
仅将M板上下移动 → 只改变极板间距离d
仅将M板左右移动 → 只改变极板正对面积S
解题思路:U恒定,d与S变化引起C变化,继而引起Q、E变化及P点的电势变化
根据电容的定义式、平行板电容器电容的决定式、匀强电场场强与电势差的关系式、电势的定义式进行综合判断
A.电容器和电源相连,电容器两端的电压不变,根据公式E=可知,将M板向上移动一小段距离,d增大,E减小,P点和N板间的电势差,不变,故P点和N板间的电势差减小,而N板的电势不变,故P点的电势降低,A项错误。
B.根据公式C=,将M板向下移动一小段距离,d减小,C变大。根据公式Q=CU可知,金属板M带电荷量增加,B项错误。
C.根据公式E=知,将M板向右移动一小段距离,d不变,E不变,所以该点电荷仍将保持静止,C项正确。
D.根据公式E=知,将M板向左移动一小段距离,d不变,E不变,所以P点和N板间的电势差不变,而N板的电势不变,故P点的电势不变,该点电荷在P点的电势能不变,D项错误。
故选C。
(智学精选)如图所示,一平行板电容器充电后与电源断开,负极板接地,两板间的P点固定一个带正电的检验电荷。用C表示电容器的电容,E表示两板间的电场强度的大小,φ表示P点的电势,Ep表示正电荷在P点的电势能。若正极板保持不动,将负极板缓慢向左平移一小段距离l0,上述各物理量与负极板移动距离x(x≤l0)的关系图像中正确的是( )
A. B.
C. D.
A、当负极板左移时,两板间的距离增加,由C=可知,C与x的图像不是一次函数图像,故A错误;
B、由U=可知:U=Q,则电场强度E==,E与d、x无关,故B错误;
C、因负极板接地,设P点开始距负极板的距离是d′,则P点的电势:φ=E(d′+x),故C正确;
D、正电荷在P点的电势能:Ep=qφ=qE(d′+x)=qEd′+qEx,所以Ep-x图像是一条倾斜的直线,故D错误。
故选:C。
电容器动态变化两类典型问题:
1.电容器始终与恒压电源相连,电容器两极板间的电势差U保持不变。
(1)根据先分析电容的变化,再由C=分析Q的变化。
(2)根据E=分析场强的变化。
(3)根据UAB=E·d=φA-φB分析某点电势变化。
2.电容器充电后与电源断开,电容器两极板所带的电荷量Q保持不变。
(1)根据先分析电容的变化,再由C=分析U的变化。
(2)根据分析场强变化。
电场中的图像问题
(智学精选)空间中存在一静电场,一电子仅在电场力作用下沿x轴正方向运动,其电势能随位置x的变化关系如图所示,则电子从x1向x3运动的过程中,下列说法正确的是( )
A.在x1处电子速度最大 B.在x2处电子加速度最大
C.在x3处电场强度最大 D.在x2处电势最高
关键信息:仅在电场力作用下 → ①只有电场力做功,电势能与动能相互转化,总量不变②电场力沿x轴方向,图线切线斜率表示该处电场力的大小
解题思路:根据可知,Ep-x图像的斜率绝对值代表静电力的大小,同时结合电场中的功能关系判断电子的动能、速度以及加速度的特征。
A.电子仅在电场力作用下运动,动能与电势能之和是恒定的,则电子从x1向x3运动的过程中,在x3处的电势能最小,则动能最大,速度最大,A错误;
B.根据可知,图象的斜率绝对值表示电子受到的电场力大小,在x2处图象的斜率为0,则电场力为0,故电子的加速度为0,B错误;
C.电子从x1向x3运动的过程中,x3处的图象斜率绝对值最大,则电场力最大,根据F=Eq可知,x3处的电场强度最大,C正确;
D.电子从x1向x3运动的过程中,电子在x2处电势能最大,但由于电子带负电,根据可知,x2处电势最低,D错误;
故选C。
(智学精选)两电荷量分别为q1和q2的点电荷放在x轴上的O、M两点,两点电荷连线上各点电势φ随x变化的关系如图所示,其中A、N两点的电势为零,ND段中C点电势最高,则( )
A.A点的电场强度大小为零
B.q1和q2带异种电荷,且q1的带电量大于q2的带电量
C.CD间的场强方向沿x轴负方向
D.将一负电荷沿x轴从N点移到D点,电势能先增大后减小
A.因为φ x图像的斜率的绝对值等于电场强度E的大小,根据图像可知,A点斜率不为零,场强不为零,故A错误;
B.由于沿着电场线方向电势降低,且A点电势为零,所以O点的电荷q1带正电,M点电荷q2带负电;由于C点合场强为零,根据公式可知,q1距离远,电荷量大,所以q1电荷量大于q2的电荷量,故B正确;
C.由图像可知从C到D电势逐渐降低,故CD间的场强方向沿x轴正方向,故C错误;
D.因为沿x轴从N点移到D点,电势先升高后降低,根据可知,负电荷从N点移到D点电势能先减小后增大,故D错误。
故选B。
电场中图像类问题的分析方法:
1.明确图像中的横轴与纵轴所代表的物理量,要区分图像中相关物理量的正负值的物理意义,要注意分析各段不同函数形式的图线所表征的物理过程;
2.要明确有关图线所包围的面积、斜率、截距所表示的物理意义,根据图像所描绘的物理过程,运用相应的物理规律计算求解;
3.同时解决此类问题要牢牢记住并理解几种常见图像的特点。
(1)φ-x图像中电场强度的大小等于φ-x图线的斜率大小,电场强度为零处,φ-x图线存在极值,其切线的斜率为零;
(2)E-x图像中图线与x轴围成的“面积”表示电势差,“面积”大小表示电势差大小,两点的电势高低根据电场方向判定;
(3)Ep-x图像中,只要粒子只受电场力作用,则,即Ep-x图像的斜率大小即为粒子所受电场力大小。
2
同课章节目录
