数学人教A版(2019)必修第一册4.4.1对数函数的概念 课件(共15张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.4.1对数函数的概念 课件(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-01 17:36:53 | ||
图片预览




文档简介
(共15张PPT)
对数函数的概念
衰减率问题
1个单位的C-13按固定年衰减率0.2衰减
1年后,衰减了多少? 保留了多少?
2年后,衰减了多少? 保留了多少?
3年后,衰减了多少? 保留了多少?
......
6.8年后,保留了多少?
0.2
0.86.8
0.83
0.8×0.2
0.82×0.2
0.82
0.8
数据验证
1.上述死亡年数和碳14含量的对应关系只针对部分数据成立吗?
2.若设生物死亡年数为n,死亡生物体内碳14含量为t,对于[0,+∞)内所有的n值和相应的t值都满足这个关系吗?
3.你能否通过计算[0,+∞)上所有的n对应的t值来验证?
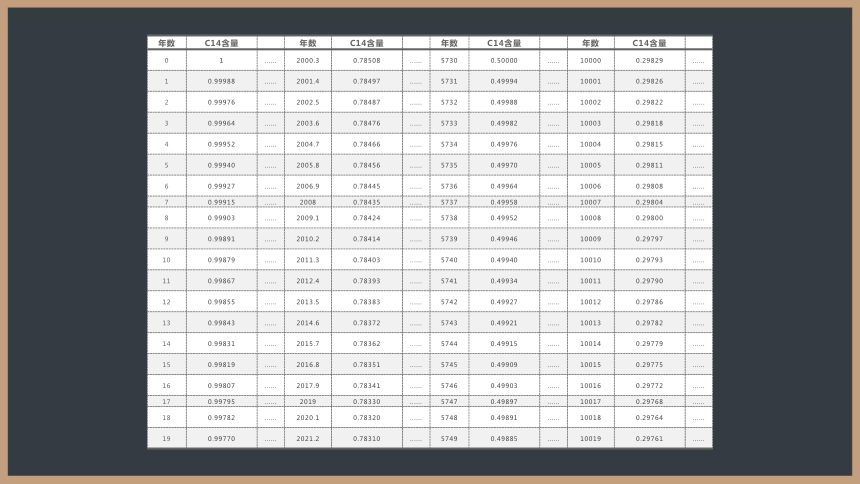
年数 C14含量 年数 C14含量 年数 C14含量 年数 C14含量
0 1 ...... 2000.3 0.78508 ...... 5730 0.50000 ...... 10000 0.29829 ......
1 0.99988 ...... 2001.4 0.78497 ...... 5731 0.49994 ...... 10001 0.29826 ......
2 0.99976 ...... 2002.5 0.78487 ...... 5732 0.49988 ...... 10002 0.29822 ......
3 0.99964 ...... 2003.6 0.78476 ...... 5733 0.49982 ...... 10003 0.29818 ......
4 0.99952 ...... 2004.7 0.78466 ...... 5734 0.49976 ...... 10004 0.29815 ......
5 0.99940 ...... 2005.8 0.78456 ...... 5735 0.49970 ...... 10005 0.29811 ......
6 0.99927 ...... 2006.9 0.78445 ...... 5736 0.49964 ...... 10006 0.29808 ......
7 0.99915 ...... 2008 0.78435 ...... 5737 0.49958 ...... 10007 0.29804 ......
8 0.99903 ...... 2009.1 0.78424 ...... 5738 0.49952 ...... 10008 0.29800 ......
9 0.99891 ...... 2010.2 0.78414 ...... 5739 0.49946 ...... 10009 0.29797 ......
10 0.99879 ...... 2011.3 0.78403 ...... 5740 0.49940 ...... 10010 0.29793 ......
11 0.99867 ...... 2012.4 0.78393 ...... 5741 0.49934 ...... 10011 0.29790 ......
12 0.99855 ...... 2013.5 0.78383 ...... 5742 0.49927 ...... 10012 0.29786 ......
13 0.99843 ...... 2014.6 0.78372 ...... 5743 0.49921 ...... 10013 0.29782 ......
14 0.99831 ...... 2015.7 0.78362 ...... 5744 0.49915 ...... 10014 0.29779 ......
15 0.99819 ...... 2016.8 0.78351 ...... 5745 0.49909 ...... 10015 0.29775 ......
16 0.99807 ...... 2017.9 0.78341 ...... 5746 0.49903 ...... 10016 0.29772 ......
17 0.99795 ...... 2019 0.78330 ...... 5747 0.49897 ...... 10017 0.29768 ......
18 0.99782 ...... 2020.1 0.78320 ...... 5748 0.49891 ...... 10018 0.29764 ......
19 0.99770 ...... 2021.2 0.78310 ...... 5749 0.49885 ...... 10019 0.29761 ......
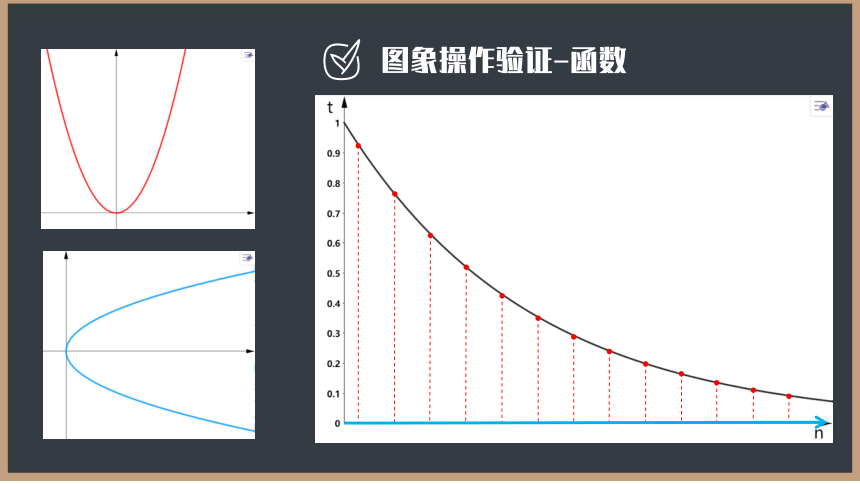
图象操作验证-函数
操作验证
1.剥离实际问题对集合A2的限制,从数学中使代数式有意义角度分析,如果将底数 换成其他不等于1的正数,集合A2和集合B2有什么变化?
2.t还是n的函数吗
操作验证
指数对数
在at=b(a>0且a≠1) 中
已知底数a和指数t求幂 指数幂运算 at
已知指数t和幂b求底数 开方运算
已知底数a和幂b求指数 对数运算 logab
数据验证
1.上述碳14含量和死亡年数的对应关系只针对部分数据成立吗?
2.若设死亡生物体内碳14含量为t,生物死亡年数为n,对于(0,1]内所有的t值和相应的n值都满足这个关系吗?3.你能否通过计算(0,1]上所有的t对应的n值来验证?
C14含量 年数 C14含量 年数 C14含量 年数 C14含量 年数
1 0 ...... 0.555 4867.293 ...... 0.355 8561.245 ...... 0.13 16865.776
0.9 870.978 ...... 0.544 5032.782 ...... 0.344 8821.447 ...... 0.129 16929.612
0.89 963.343 ...... 0.533 5201.651 ...... 0.333 9090.106 ...... 0.128 16993.944
0.88 1056.753 ...... 0.522 5374.043 ...... 0.322 9367.790 ...... 0.127 17058.781
0.87 1151.230 ...... 0.511 5550.106 ...... 0.311 9655.127 ...... 0.126 17124.130
0.86 1246.799 ...... 0.5 5730 ...... 0.3 9952.813 ...... 0.125 17190
0.85 1343.486 ...... 0.489 5913.896 ...... 0.289 10261.620 ...... 0.124 17256.399
0.84 1441.317 ...... 0.478 6101.977 ...... 0.278 10582.412 ...... 0.123 17323.336
0.83 1540.320 ...... 0.467 6294.437 ...... 0.267 10916.156 ...... 0.122 17390.819
0.82 1640.523 ...... 0.456 6491.484 ...... 0.256 11263.944 ...... 0.121 17458.858
0.81 1741.955 ...... 0.445 6693.343 ...... 0.245 11627.009 ...... 0.12 17527.461
0.8 1844.648 ...... 0.434 6900.255 ...... 0.234 12006.754 ...... 0.119 17596.638
0.79 1948.632 ...... 0.423 7112.480 ...... 0.223 12404.788 ...... 0.118 17666.399
0.78 2053.941 ...... 0.412 7330.296 ...... 0.212 12822.960 ...... 0.117 17736.754
0.77 2160.609 ...... 0.401 7554.007 ...... 0.201 13263.418 ...... 0.116 17807.713
0.76 2268.671 ...... 0.39 7783.941 ...... 0.19 13728.671 ...... 0.115 17879.286
0.75 2378.165 ...... 0.379 8020.454 ...... 0.179 14221.680 ...... 0.114 17951.484
0.74 2489.128 ...... 0.368 8263.934 ...... 0.168 14745.965 ...... 0.113 18024.318
0.73 2601.601 ...... 0.357 8514.803 ...... 0.157 15305.767 ...... 0.112 18097.800
0.72 2715.626 ...... 0.346 8773.524 ...... 0.146 15906.249 ...... 0.111 18171.941
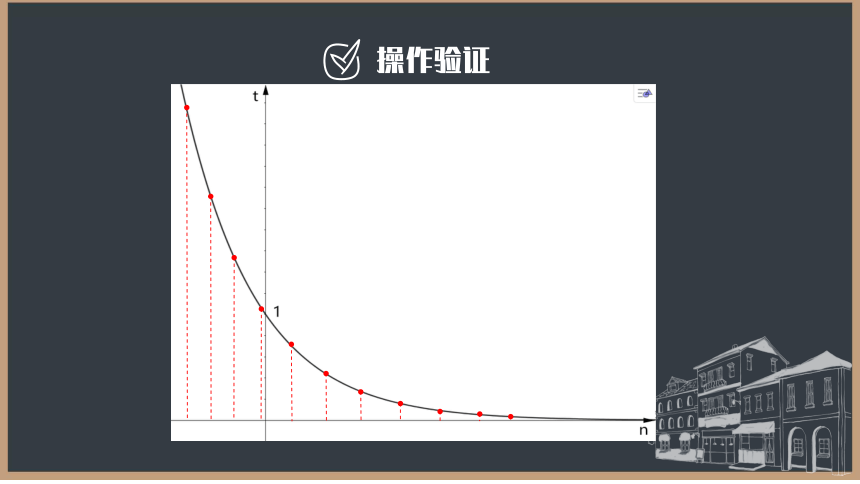
操作验证
操作验证
1.剥离实际问题对集合B3的限制,从数学的使代数式有意义角度分析,如果将底数 换成其他实数,底数有什么限制?集合B3和集合A3有什么变化?
2.n还是t的函数吗
操作验证
对数函数和指数函数关联
指数函数 对数函数
对应关系
定义域
值域
y=ax(a>0且a≠1)
R
(0,+∞)
y=logax(a>0且a≠1)
R
(0,+∞)
谢谢观看
对数函数的概念
衰减率问题
1个单位的C-13按固定年衰减率0.2衰减
1年后,衰减了多少? 保留了多少?
2年后,衰减了多少? 保留了多少?
3年后,衰减了多少? 保留了多少?
......
6.8年后,保留了多少?
0.2
0.86.8
0.83
0.8×0.2
0.82×0.2
0.82
0.8
数据验证
1.上述死亡年数和碳14含量的对应关系只针对部分数据成立吗?
2.若设生物死亡年数为n,死亡生物体内碳14含量为t,对于[0,+∞)内所有的n值和相应的t值都满足这个关系吗?
3.你能否通过计算[0,+∞)上所有的n对应的t值来验证?
年数 C14含量 年数 C14含量 年数 C14含量 年数 C14含量
0 1 ...... 2000.3 0.78508 ...... 5730 0.50000 ...... 10000 0.29829 ......
1 0.99988 ...... 2001.4 0.78497 ...... 5731 0.49994 ...... 10001 0.29826 ......
2 0.99976 ...... 2002.5 0.78487 ...... 5732 0.49988 ...... 10002 0.29822 ......
3 0.99964 ...... 2003.6 0.78476 ...... 5733 0.49982 ...... 10003 0.29818 ......
4 0.99952 ...... 2004.7 0.78466 ...... 5734 0.49976 ...... 10004 0.29815 ......
5 0.99940 ...... 2005.8 0.78456 ...... 5735 0.49970 ...... 10005 0.29811 ......
6 0.99927 ...... 2006.9 0.78445 ...... 5736 0.49964 ...... 10006 0.29808 ......
7 0.99915 ...... 2008 0.78435 ...... 5737 0.49958 ...... 10007 0.29804 ......
8 0.99903 ...... 2009.1 0.78424 ...... 5738 0.49952 ...... 10008 0.29800 ......
9 0.99891 ...... 2010.2 0.78414 ...... 5739 0.49946 ...... 10009 0.29797 ......
10 0.99879 ...... 2011.3 0.78403 ...... 5740 0.49940 ...... 10010 0.29793 ......
11 0.99867 ...... 2012.4 0.78393 ...... 5741 0.49934 ...... 10011 0.29790 ......
12 0.99855 ...... 2013.5 0.78383 ...... 5742 0.49927 ...... 10012 0.29786 ......
13 0.99843 ...... 2014.6 0.78372 ...... 5743 0.49921 ...... 10013 0.29782 ......
14 0.99831 ...... 2015.7 0.78362 ...... 5744 0.49915 ...... 10014 0.29779 ......
15 0.99819 ...... 2016.8 0.78351 ...... 5745 0.49909 ...... 10015 0.29775 ......
16 0.99807 ...... 2017.9 0.78341 ...... 5746 0.49903 ...... 10016 0.29772 ......
17 0.99795 ...... 2019 0.78330 ...... 5747 0.49897 ...... 10017 0.29768 ......
18 0.99782 ...... 2020.1 0.78320 ...... 5748 0.49891 ...... 10018 0.29764 ......
19 0.99770 ...... 2021.2 0.78310 ...... 5749 0.49885 ...... 10019 0.29761 ......
图象操作验证-函数
操作验证
1.剥离实际问题对集合A2的限制,从数学中使代数式有意义角度分析,如果将底数 换成其他不等于1的正数,集合A2和集合B2有什么变化?
2.t还是n的函数吗
操作验证
指数对数
在at=b(a>0且a≠1) 中
已知底数a和指数t求幂 指数幂运算 at
已知指数t和幂b求底数 开方运算
已知底数a和幂b求指数 对数运算 logab
数据验证
1.上述碳14含量和死亡年数的对应关系只针对部分数据成立吗?
2.若设死亡生物体内碳14含量为t,生物死亡年数为n,对于(0,1]内所有的t值和相应的n值都满足这个关系吗?3.你能否通过计算(0,1]上所有的t对应的n值来验证?
C14含量 年数 C14含量 年数 C14含量 年数 C14含量 年数
1 0 ...... 0.555 4867.293 ...... 0.355 8561.245 ...... 0.13 16865.776
0.9 870.978 ...... 0.544 5032.782 ...... 0.344 8821.447 ...... 0.129 16929.612
0.89 963.343 ...... 0.533 5201.651 ...... 0.333 9090.106 ...... 0.128 16993.944
0.88 1056.753 ...... 0.522 5374.043 ...... 0.322 9367.790 ...... 0.127 17058.781
0.87 1151.230 ...... 0.511 5550.106 ...... 0.311 9655.127 ...... 0.126 17124.130
0.86 1246.799 ...... 0.5 5730 ...... 0.3 9952.813 ...... 0.125 17190
0.85 1343.486 ...... 0.489 5913.896 ...... 0.289 10261.620 ...... 0.124 17256.399
0.84 1441.317 ...... 0.478 6101.977 ...... 0.278 10582.412 ...... 0.123 17323.336
0.83 1540.320 ...... 0.467 6294.437 ...... 0.267 10916.156 ...... 0.122 17390.819
0.82 1640.523 ...... 0.456 6491.484 ...... 0.256 11263.944 ...... 0.121 17458.858
0.81 1741.955 ...... 0.445 6693.343 ...... 0.245 11627.009 ...... 0.12 17527.461
0.8 1844.648 ...... 0.434 6900.255 ...... 0.234 12006.754 ...... 0.119 17596.638
0.79 1948.632 ...... 0.423 7112.480 ...... 0.223 12404.788 ...... 0.118 17666.399
0.78 2053.941 ...... 0.412 7330.296 ...... 0.212 12822.960 ...... 0.117 17736.754
0.77 2160.609 ...... 0.401 7554.007 ...... 0.201 13263.418 ...... 0.116 17807.713
0.76 2268.671 ...... 0.39 7783.941 ...... 0.19 13728.671 ...... 0.115 17879.286
0.75 2378.165 ...... 0.379 8020.454 ...... 0.179 14221.680 ...... 0.114 17951.484
0.74 2489.128 ...... 0.368 8263.934 ...... 0.168 14745.965 ...... 0.113 18024.318
0.73 2601.601 ...... 0.357 8514.803 ...... 0.157 15305.767 ...... 0.112 18097.800
0.72 2715.626 ...... 0.346 8773.524 ...... 0.146 15906.249 ...... 0.111 18171.941
操作验证
操作验证
1.剥离实际问题对集合B3的限制,从数学的使代数式有意义角度分析,如果将底数 换成其他实数,底数有什么限制?集合B3和集合A3有什么变化?
2.n还是t的函数吗
操作验证
对数函数和指数函数关联
指数函数 对数函数
对应关系
定义域
值域
y=ax(a>0且a≠1)
R
(0,+∞)
y=logax(a>0且a≠1)
R
(0,+∞)
谢谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
