鲁教版(五四学制)九年级数学上册第2章直角三角形的边角关系 单元综合达标测试题(含解析)
文档属性
| 名称 | 鲁教版(五四学制)九年级数学上册第2章直角三角形的边角关系 单元综合达标测试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 432.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-01 10:09:08 | ||
图片预览



文档简介
2022-2023学年鲁教版(五四学制)九年级数学上册《第2章直角三角形的边角关系》
单元综合达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanA的值为( )
A. B. C. D.
2.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为( )
A.6 B.6 C.12 D.8
3.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
4.王明同学遇到了这样一道题,,则锐角α的度数为( )
A.40° B.30° C.20° D.10°
5.已知AD是△ABC的中线,BC=6,且∠ADC=45°,∠B=30°,则AC=( )
A. B. C. D.6
6.如图,在4×4正方形网格中,点A,B,C为网格交点,AD⊥BC,垂足为D,则sin∠BAD的值为( )
A. B. C. D.
7.如图,在Rt△BAD中,延长斜边BD到点C,使,连接AC,若,则tan∠CAD的值( )
A. B. C. D.
8.一艘货轮B在灯塔A的南偏西60°方向,距离A点海里,货轮B沿北偏东15°航行一段距离后到达C地,此时AC距离海里,判断C在A的北偏西多少度( )
A.60° B.30° C.15° D.45°
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,则BC= .
10.在锐角△ABC中,若,则∠C的度数是 度.
11.如图,在矩形ABCD中,E为AD上的点,AE=AB,BE=DE,则tan∠BDE= .
12.如图,已知在△ABC中,∠BAC=45°,BC=4.若∠B=45°,则AB= ;
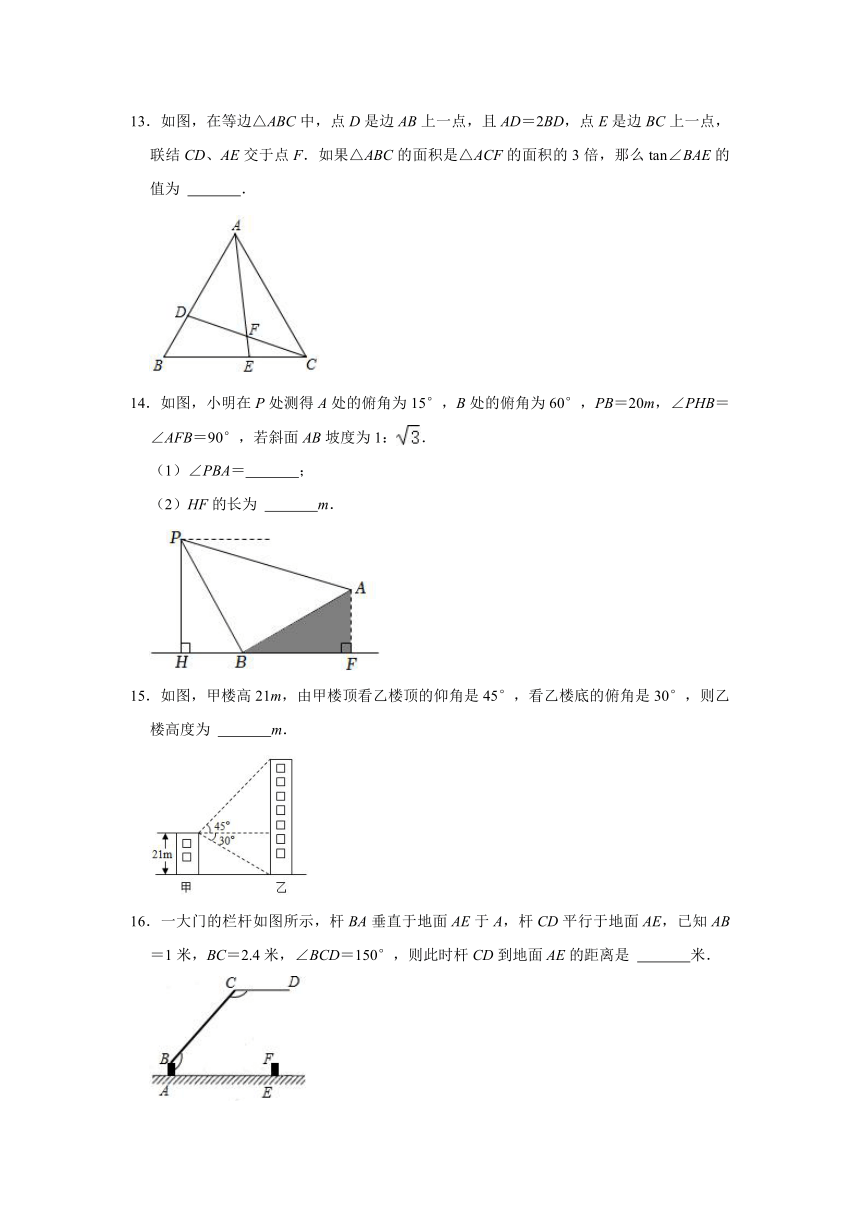
13.如图,在等边△ABC中,点D是边AB上一点,且AD=2BD,点E是边BC上一点,联结CD、AE交于点F.如果△ABC的面积是△ACF的面积的3倍,那么tan∠BAE的值为 .
14.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,PB=20m,∠PHB=∠AFB=90°,若斜面AB坡度为1:.
(1)∠PBA= ;
(2)HF的长为 m.
15.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度为 m.
16.一大门的栏杆如图所示,杆BA垂直于地面AE于A,杆CD平行于地面AE,已知AB=1米,BC=2.4米,∠BCD=150°,则此时杆CD到地面AE的距离是 米.
三.解答题(共6小题,满分40分)
17.如图,在Rt△ABC中,∠C=90°,AB=15,sin∠A=,求BC的长和tan∠B的值.
18.计算:﹣2cos30°+6sin245°.
19.如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且ED=BF,连接AF,CE,AC,EF,且AC与EF相交于点O.
(1)求证:四边形AFCE是平行四边形;
(2)若AC平分∠FAE,AC=8,tan∠DAC=,求四边形AFCE的面积.
20.如图,在Rt△ABC中,∠A=90°,点D,E、F分别为AB,AC,BC的中点,连接DF,EF.
(1)求证:四边形AEFD是矩形;
(2)连接BE,若AB=2,tanC=,求BE的长.
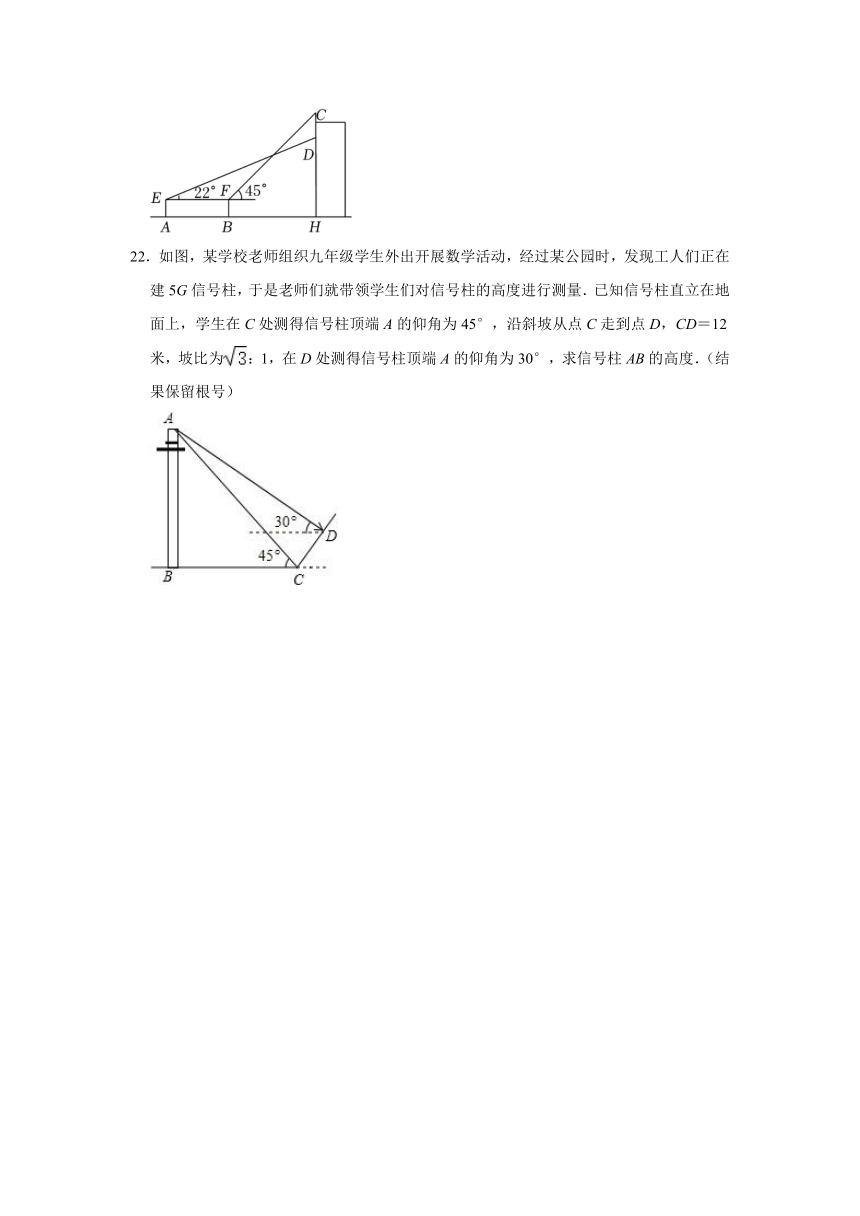
21.如图,某小区的物业楼上悬挂一块高为3m的广告牌,即CD=3m.小奇和小妙要测量广告牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小奇在E处测得广告牌底部点D的仰角为22°,小妙在F处测得广告牌顶部点C的仰角为45°,AB=9m,请根据相关测量信息,求出广告牌底部点D到地面的距离DH的长.(图中点A,B,C,D,E,F,H在同一平面内.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
22.如图,某学校老师组织九年级学生外出开展数学活动,经过某公园时,发现工人们正在建5G信号柱,于是老师们就带领学生们对信号柱的高度进行测量.已知信号柱直立在地面上,学生在C处测得信号柱顶端A的仰角为45°,沿斜坡从点C走到点D,CD=12米,坡比为:1,在D处测得信号柱顶端A的仰角为30°,求信号柱AB的高度.(结果保留根号)
参考答案
一.选择题(共8小题,满分40分)
1.解:在Rt△ABC中,∠C=90°,BC=12,AC=5,
∴tanA==.
故选:D.
2.解:∵点A的坐标为(0,3),
∴AO=3,
∵tan∠ABO=,
∴=,
∴=,
∴BO=,
∵△AOB是直角三角形,
∴AB====2,
∵菱形的四条边相等,
∴菱形ABCD的周长为2×4=8.
故选:D.
3.解:如图,过点P作PQ⊥x轴于点Q,
∵OP∥AB,
∴∠CAB=∠CPO,∠ABC=∠COP,
∴△OCP∽△BCA,
∴CP:AC=OC:BC=1:2,
∵∠AOC=∠AQP=90°,
∴CO∥PQ,
∴OQ:AO=CP:AC=1:2,
∵P(1,1),
∴PQ=OQ=1,
∴AO=2,
∴tan∠OAP===.
故选:C.
4.解:∵tan30°=,
∴tan30°=1,
∵tan(α+10°)=1,
∴α+10°=30°,
∴α=20°,
故选:C.
5.解:如图,过点A作AE⊥BC,垂足为E,
∵∠ADC=45°,∠B=30°,
∴AB=2AE,AE=ED,
∵BC=6,AD是△ABC的中线,
∴CD=BD=3,
设AE=DE=x,则AB=2x,
∴CE=x﹣3,BE=x+3,
在Rt△AEB中,根据勾股定理得,
(2x)2=x2+(x+3)2,
∴2x2﹣6x=9,
在Rt△AEC中,根据勾股定理得,
AC2=x2+(x﹣3)2,
∴AC2=2x2﹣6x+9,
∴AC2=18,
∴AC=3(负值舍去).
故选:B.
6.解:如图,连接AC,
在Rt△BEC中,BC==5,
∵AD⊥BC,
∴=8,
即,
解得AD=,
在Rt△ADB中,BD=,
∴sin∠BAD=.
故选:C.
7.解:过点C作CE垂直AD的延长线于E,
在Rt△BAD中,,
∴,
设AB=3a,AD=4a,
则BD==5a,
∵CE⊥AE,BA⊥AD,
∴△BAD∽△CED,
∴,
∵DC=BD,
∴DE=AD=2a,CE=AB=a,
∴在Rt△AEC中,tan∠CAD==.
故选:B.
8.解:如图,过A作AD⊥BC于D.
由题意可得∠GAB=60°,AB=30海里,∠EBC=15°,AC=20海里.
∵BE∥FG,
∴∠EBA=∠GAB=60°,
∴∠ABD=∠EBA﹣∠EBC=60°﹣15°=45°,
在Rt△ABD中,∠ADB=90°,
∴AD=BD=AB=30,∠DAB=45°,
∴∠DAH=∠DAB﹣∠HAB=45°﹣(90°﹣60°)=15°.
在Rt△ACD中,∠ADC=90°,
∴CD===10,
∴tan∠CAD===,
∴∠CAD=30°,
∴∠FAC=90°﹣∠CAD﹣∠DAH=90°﹣30°﹣15°=45°,
∴C在A的北偏西45度.
故选:D.
二.填空题(共8小题,满分40分)
9.解:在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,
∴BC=AC sinA=200×0.6=120,
故答案为:120.
10.解:∵,
∴sinA﹣=0,cosB﹣=0,
则sinA=,cosB=,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为:75.
11.解:∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=AE,
设AB=a,则AE=a,BE==a=ED,
∴AD=AE+DE=(+1)a,
在Rt△ABD中,tan∠BDE===﹣1,
故答案为:﹣1.
12.解:(1)∵∠BAC=45°,∠B=45°,
∴∠BAC=∠B=45°,
∴BC=AC=4,∠ACB=90°,
∴AB=,
故答案为:;
13.解:如图,取AD中点G,连接FG,过点F作FH⊥AB于点H,
设等边△ABC的边长为12a,则高为6a,
∴S△ABC=×12a×6a=36a2,
∵AB=AC=12a,
∴AD=8a,AG=4a,
∴S△ACD=×8a×6a=24a2,
∵△ABC的面积是△ACF的面积的3倍,
∴S△ACF=×36a2=12a2,
∴S△ADF=S△ACD﹣S△ACF=12a2,
∵S△ADF=×8a×HF,
∴×8a×HF=12a2,
∴HF=3a,
∴点F为CD中点,
∴FG为△ACD的中位线,
∴FG=6a,
在Rt△HFG中,由勾股定理可得:
HG=,
即HG==3a,
∴AH=AG+HG=7a,
∴tan∠BAE===,
故答案为:.
14.解:(1)如图:
由题意得:
∠CPB=60°,∠CPA=15°,PC∥HF,
∴∠CPB=∠PBH=60°,
∵斜面AB坡度为1:,
∴==,
在Rt△ABF中,tan∠ABF==,
∴∠ABF=30°,
∴∠PBA=180°﹣∠ABF﹣∠PBH=90°,
故答案为:90°;
(2)在Rt△PBH中,PB=20m,∠PBH=60°,
∴BH=PB cos60°=20×=10(m),
∵∠CPB=60°,∠CPA=15°,
∴∠APB=∠CPB﹣∠CPA=45°,
∵∠PBA=90°,
∴AB=PB tan45°=20(m),
在Rt△ABF中,∠ABF=30°,
∴BF=AB cos30°=20×=10(m),
∴HF=HB+BF=(10+10)m,
故答案为:(10+10).
15.解:如图:
由题意得:
AB=CE=21m,∠AEC=∠AED=90°,
在Rt△AEC中,∠CAE=30°,
∴AE===21(m),
在Rt△AED中,∠DAE=45°,
∴DE=AE tan45°=21(m),
∴DC=DE+CD=(21+21)m,
∴乙楼高度为(21+21)m,
故答案为:(21+21).
16.解:过点C作CG⊥AE于点G,过点B作BH⊥CG于点H,如图:
∵CG⊥AE,BH⊥CG,
∴∠AGC=90°,
∴∠BHC=90°,
∴∠AGC=∠BHC,
∴BH∥AE,
∵CD∥AE,
∴CD∥BH,
∴∠CBH+∠BCD=180°,
∵∠BCD=150°,
∴∠CBH=30°,
∴CH=BC,
∵BC=2.4米,
∴CH=1.2米,
∵BA⊥AE,CG⊥AE,BH⊥CG
∴四边形ABHG是矩形,
∴HG=AB=1米,
∴CG=CH+HG=1.2+12.2(米).
答:杆CD到地面AE的距离是2.2米.
故答案为:2.2.
三.解答题(共6小题,满分40分)
17.解:∵sin∠A=,
∴=,
∵AB=15,
∴BC=9;
∴AC==12,
∴tan∠B===.
18.解:原式=﹣2×+6×()2
=﹣+6×
=﹣1﹣+3
=2.
19.(1)证明:∵在平行四边形ABCD中,
AD=BC.AE∥FC,
∵ED=BF,
∴AD﹣ED=BC﹣BF,
∴AE=FC,
∴四边形AFCE是平行四边形;
(2)解:∵AE∥FC,
∴∠EAC=∠ACF,
∴∠EAC=∠FAC,
∴∠ACF=∠FAC,
∴AF=FC,
∵四边形AFCE是平行四边形,
∴平行四边形AFCE是菱形,
∴AO=AC=4,AC⊥EF,
在Rt△AOE中,AO=4,tan∠DAC=,
∴EO=3,
∴S△AEO=AO EO=6,
S菱形=4S△AEO=24.
20.(1)证明:∵点D,E、F分别为AB,AC,BC的中点,
∴DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∵∠A=90°,
∴四边形AEFD是矩形;
(2)解:∵∠A=90°,AB=2,tanC=,
∴=,
即=,
解得AC=4,
∵点E为AC的中点,
∴AE=2,
∴BE===2,
即BE的长是2.
21.解:延长EF交CH于N,
则EF=AB=9m,∠CNF=90°,
∵∠CFN=45°,
∴CN=NF,
设DN=xm,
∵CD=3m,
∴NF=CN=CD+DN=(x+3)m,
∴EN=EF+FN=9+(x+3)=(x+12)m,
在Rt△DNE中,∠DEN=22°,
∴DN=EN tan22°≈0.4(x+12),
∴0.4(x+12)=x,
解得:x=8,
∴DN=8m,
∴DH=DN+NH=8+1.2=9.2(m),
答:点D到地面的距离DH的长约为9.2m.
22.解:过点D作DE⊥BC,交BC的延长线于点E,过点D作DF⊥AB,垂足为F,
则BF=DE,DF=BE,
设BC=x米,
在Rt△ABC中,∠ACB=45°,
∴AB=BC tan45°=x(米),
∵斜坡CD的坡比为:1,
∴=,
在Rt△DCE中,tan∠DCE==,
∴∠DCE=60°,
∴DE=CD sin60°=12×=6(米),
CE=CD cos60°=12×=6(米),
∴DF=BE=BC+CE=(x+6)米,
AF=AB﹣BF=AB﹣DE=(x﹣6)米,
在Rt△ADF中,∠ADF=30°,
∴tan30°===,
∴x=12+12,
经检验:x=12+12是原方程的根,
∴AB=(12+12)米,
∴信号柱AB的高度为(12+12)米.
单元综合达标测试题(附答案)
一.选择题(共8小题,满分40分)
1.在Rt△ABC中,∠C=90°,BC=12,AC=5,则tanA的值为( )
A. B. C. D.
2.如图,在平面直角坐标系中,菱形ABCD的顶点A,B,C在坐标轴上,若点A的坐标为(0,3),tan∠ABO=,则菱形ABCD的周长为( )
A.6 B.6 C.12 D.8
3.如图,在平面直角坐标系中,点A,B分别在x轴负半轴和y轴正半轴上,点C在OB上,OC:BC=1:2,连接AC,过点O作OP∥AB交AC的延长线于P.若P(1,1),则tan∠OAP的值是( )
A. B. C. D.3
4.王明同学遇到了这样一道题,,则锐角α的度数为( )
A.40° B.30° C.20° D.10°
5.已知AD是△ABC的中线,BC=6,且∠ADC=45°,∠B=30°,则AC=( )
A. B. C. D.6
6.如图,在4×4正方形网格中,点A,B,C为网格交点,AD⊥BC,垂足为D,则sin∠BAD的值为( )
A. B. C. D.
7.如图,在Rt△BAD中,延长斜边BD到点C,使,连接AC,若,则tan∠CAD的值( )
A. B. C. D.
8.一艘货轮B在灯塔A的南偏西60°方向,距离A点海里,货轮B沿北偏东15°航行一段距离后到达C地,此时AC距离海里,判断C在A的北偏西多少度( )
A.60° B.30° C.15° D.45°
二.填空题(共8小题,满分40分)
9.在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,则BC= .
10.在锐角△ABC中,若,则∠C的度数是 度.
11.如图,在矩形ABCD中,E为AD上的点,AE=AB,BE=DE,则tan∠BDE= .
12.如图,已知在△ABC中,∠BAC=45°,BC=4.若∠B=45°,则AB= ;
13.如图,在等边△ABC中,点D是边AB上一点,且AD=2BD,点E是边BC上一点,联结CD、AE交于点F.如果△ABC的面积是△ACF的面积的3倍,那么tan∠BAE的值为 .
14.如图,小明在P处测得A处的俯角为15°,B处的俯角为60°,PB=20m,∠PHB=∠AFB=90°,若斜面AB坡度为1:.
(1)∠PBA= ;
(2)HF的长为 m.
15.如图,甲楼高21m,由甲楼顶看乙楼顶的仰角是45°,看乙楼底的俯角是30°,则乙楼高度为 m.
16.一大门的栏杆如图所示,杆BA垂直于地面AE于A,杆CD平行于地面AE,已知AB=1米,BC=2.4米,∠BCD=150°,则此时杆CD到地面AE的距离是 米.
三.解答题(共6小题,满分40分)
17.如图,在Rt△ABC中,∠C=90°,AB=15,sin∠A=,求BC的长和tan∠B的值.
18.计算:﹣2cos30°+6sin245°.
19.如图,在平行四边形ABCD中,点E,F分别在AD,BC上,且ED=BF,连接AF,CE,AC,EF,且AC与EF相交于点O.
(1)求证:四边形AFCE是平行四边形;
(2)若AC平分∠FAE,AC=8,tan∠DAC=,求四边形AFCE的面积.
20.如图,在Rt△ABC中,∠A=90°,点D,E、F分别为AB,AC,BC的中点,连接DF,EF.
(1)求证:四边形AEFD是矩形;
(2)连接BE,若AB=2,tanC=,求BE的长.
21.如图,某小区的物业楼上悬挂一块高为3m的广告牌,即CD=3m.小奇和小妙要测量广告牌的底部点D到地面的距离.测角仪支架高AE=BF=1.2m,小奇在E处测得广告牌底部点D的仰角为22°,小妙在F处测得广告牌顶部点C的仰角为45°,AB=9m,请根据相关测量信息,求出广告牌底部点D到地面的距离DH的长.(图中点A,B,C,D,E,F,H在同一平面内.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)
22.如图,某学校老师组织九年级学生外出开展数学活动,经过某公园时,发现工人们正在建5G信号柱,于是老师们就带领学生们对信号柱的高度进行测量.已知信号柱直立在地面上,学生在C处测得信号柱顶端A的仰角为45°,沿斜坡从点C走到点D,CD=12米,坡比为:1,在D处测得信号柱顶端A的仰角为30°,求信号柱AB的高度.(结果保留根号)
参考答案
一.选择题(共8小题,满分40分)
1.解:在Rt△ABC中,∠C=90°,BC=12,AC=5,
∴tanA==.
故选:D.
2.解:∵点A的坐标为(0,3),
∴AO=3,
∵tan∠ABO=,
∴=,
∴=,
∴BO=,
∵△AOB是直角三角形,
∴AB====2,
∵菱形的四条边相等,
∴菱形ABCD的周长为2×4=8.
故选:D.
3.解:如图,过点P作PQ⊥x轴于点Q,
∵OP∥AB,
∴∠CAB=∠CPO,∠ABC=∠COP,
∴△OCP∽△BCA,
∴CP:AC=OC:BC=1:2,
∵∠AOC=∠AQP=90°,
∴CO∥PQ,
∴OQ:AO=CP:AC=1:2,
∵P(1,1),
∴PQ=OQ=1,
∴AO=2,
∴tan∠OAP===.
故选:C.
4.解:∵tan30°=,
∴tan30°=1,
∵tan(α+10°)=1,
∴α+10°=30°,
∴α=20°,
故选:C.
5.解:如图,过点A作AE⊥BC,垂足为E,
∵∠ADC=45°,∠B=30°,
∴AB=2AE,AE=ED,
∵BC=6,AD是△ABC的中线,
∴CD=BD=3,
设AE=DE=x,则AB=2x,
∴CE=x﹣3,BE=x+3,
在Rt△AEB中,根据勾股定理得,
(2x)2=x2+(x+3)2,
∴2x2﹣6x=9,
在Rt△AEC中,根据勾股定理得,
AC2=x2+(x﹣3)2,
∴AC2=2x2﹣6x+9,
∴AC2=18,
∴AC=3(负值舍去).
故选:B.
6.解:如图,连接AC,
在Rt△BEC中,BC==5,
∵AD⊥BC,
∴=8,
即,
解得AD=,
在Rt△ADB中,BD=,
∴sin∠BAD=.
故选:C.
7.解:过点C作CE垂直AD的延长线于E,
在Rt△BAD中,,
∴,
设AB=3a,AD=4a,
则BD==5a,
∵CE⊥AE,BA⊥AD,
∴△BAD∽△CED,
∴,
∵DC=BD,
∴DE=AD=2a,CE=AB=a,
∴在Rt△AEC中,tan∠CAD==.
故选:B.
8.解:如图,过A作AD⊥BC于D.
由题意可得∠GAB=60°,AB=30海里,∠EBC=15°,AC=20海里.
∵BE∥FG,
∴∠EBA=∠GAB=60°,
∴∠ABD=∠EBA﹣∠EBC=60°﹣15°=45°,
在Rt△ABD中,∠ADB=90°,
∴AD=BD=AB=30,∠DAB=45°,
∴∠DAH=∠DAB﹣∠HAB=45°﹣(90°﹣60°)=15°.
在Rt△ACD中,∠ADC=90°,
∴CD===10,
∴tan∠CAD===,
∴∠CAD=30°,
∴∠FAC=90°﹣∠CAD﹣∠DAH=90°﹣30°﹣15°=45°,
∴C在A的北偏西45度.
故选:D.
二.填空题(共8小题,满分40分)
9.解:在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,
∴BC=AC sinA=200×0.6=120,
故答案为:120.
10.解:∵,
∴sinA﹣=0,cosB﹣=0,
则sinA=,cosB=,
∴∠A=60°,∠B=45°,
∴∠C=180°﹣60°﹣45°=75°.
故答案为:75.
11.解:∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=AE,
设AB=a,则AE=a,BE==a=ED,
∴AD=AE+DE=(+1)a,
在Rt△ABD中,tan∠BDE===﹣1,
故答案为:﹣1.
12.解:(1)∵∠BAC=45°,∠B=45°,
∴∠BAC=∠B=45°,
∴BC=AC=4,∠ACB=90°,
∴AB=,
故答案为:;
13.解:如图,取AD中点G,连接FG,过点F作FH⊥AB于点H,
设等边△ABC的边长为12a,则高为6a,
∴S△ABC=×12a×6a=36a2,
∵AB=AC=12a,
∴AD=8a,AG=4a,
∴S△ACD=×8a×6a=24a2,
∵△ABC的面积是△ACF的面积的3倍,
∴S△ACF=×36a2=12a2,
∴S△ADF=S△ACD﹣S△ACF=12a2,
∵S△ADF=×8a×HF,
∴×8a×HF=12a2,
∴HF=3a,
∴点F为CD中点,
∴FG为△ACD的中位线,
∴FG=6a,
在Rt△HFG中,由勾股定理可得:
HG=,
即HG==3a,
∴AH=AG+HG=7a,
∴tan∠BAE===,
故答案为:.
14.解:(1)如图:
由题意得:
∠CPB=60°,∠CPA=15°,PC∥HF,
∴∠CPB=∠PBH=60°,
∵斜面AB坡度为1:,
∴==,
在Rt△ABF中,tan∠ABF==,
∴∠ABF=30°,
∴∠PBA=180°﹣∠ABF﹣∠PBH=90°,
故答案为:90°;
(2)在Rt△PBH中,PB=20m,∠PBH=60°,
∴BH=PB cos60°=20×=10(m),
∵∠CPB=60°,∠CPA=15°,
∴∠APB=∠CPB﹣∠CPA=45°,
∵∠PBA=90°,
∴AB=PB tan45°=20(m),
在Rt△ABF中,∠ABF=30°,
∴BF=AB cos30°=20×=10(m),
∴HF=HB+BF=(10+10)m,
故答案为:(10+10).
15.解:如图:
由题意得:
AB=CE=21m,∠AEC=∠AED=90°,
在Rt△AEC中,∠CAE=30°,
∴AE===21(m),
在Rt△AED中,∠DAE=45°,
∴DE=AE tan45°=21(m),
∴DC=DE+CD=(21+21)m,
∴乙楼高度为(21+21)m,
故答案为:(21+21).
16.解:过点C作CG⊥AE于点G,过点B作BH⊥CG于点H,如图:
∵CG⊥AE,BH⊥CG,
∴∠AGC=90°,
∴∠BHC=90°,
∴∠AGC=∠BHC,
∴BH∥AE,
∵CD∥AE,
∴CD∥BH,
∴∠CBH+∠BCD=180°,
∵∠BCD=150°,
∴∠CBH=30°,
∴CH=BC,
∵BC=2.4米,
∴CH=1.2米,
∵BA⊥AE,CG⊥AE,BH⊥CG
∴四边形ABHG是矩形,
∴HG=AB=1米,
∴CG=CH+HG=1.2+12.2(米).
答:杆CD到地面AE的距离是2.2米.
故答案为:2.2.
三.解答题(共6小题,满分40分)
17.解:∵sin∠A=,
∴=,
∵AB=15,
∴BC=9;
∴AC==12,
∴tan∠B===.
18.解:原式=﹣2×+6×()2
=﹣+6×
=﹣1﹣+3
=2.
19.(1)证明:∵在平行四边形ABCD中,
AD=BC.AE∥FC,
∵ED=BF,
∴AD﹣ED=BC﹣BF,
∴AE=FC,
∴四边形AFCE是平行四边形;
(2)解:∵AE∥FC,
∴∠EAC=∠ACF,
∴∠EAC=∠FAC,
∴∠ACF=∠FAC,
∴AF=FC,
∵四边形AFCE是平行四边形,
∴平行四边形AFCE是菱形,
∴AO=AC=4,AC⊥EF,
在Rt△AOE中,AO=4,tan∠DAC=,
∴EO=3,
∴S△AEO=AO EO=6,
S菱形=4S△AEO=24.
20.(1)证明:∵点D,E、F分别为AB,AC,BC的中点,
∴DF∥AE,DF=AE,
∴四边形AEFD是平行四边形,
∵∠A=90°,
∴四边形AEFD是矩形;
(2)解:∵∠A=90°,AB=2,tanC=,
∴=,
即=,
解得AC=4,
∵点E为AC的中点,
∴AE=2,
∴BE===2,
即BE的长是2.
21.解:延长EF交CH于N,
则EF=AB=9m,∠CNF=90°,
∵∠CFN=45°,
∴CN=NF,
设DN=xm,
∵CD=3m,
∴NF=CN=CD+DN=(x+3)m,
∴EN=EF+FN=9+(x+3)=(x+12)m,
在Rt△DNE中,∠DEN=22°,
∴DN=EN tan22°≈0.4(x+12),
∴0.4(x+12)=x,
解得:x=8,
∴DN=8m,
∴DH=DN+NH=8+1.2=9.2(m),
答:点D到地面的距离DH的长约为9.2m.
22.解:过点D作DE⊥BC,交BC的延长线于点E,过点D作DF⊥AB,垂足为F,
则BF=DE,DF=BE,
设BC=x米,
在Rt△ABC中,∠ACB=45°,
∴AB=BC tan45°=x(米),
∵斜坡CD的坡比为:1,
∴=,
在Rt△DCE中,tan∠DCE==,
∴∠DCE=60°,
∴DE=CD sin60°=12×=6(米),
CE=CD cos60°=12×=6(米),
∴DF=BE=BC+CE=(x+6)米,
AF=AB﹣BF=AB﹣DE=(x﹣6)米,
在Rt△ADF中,∠ADF=30°,
∴tan30°===,
∴x=12+12,
经检验:x=12+12是原方程的根,
∴AB=(12+12)米,
∴信号柱AB的高度为(12+12)米.
