北师大版八年级数学下册第3章 图形的平移与旋转 检测题(含解析)
文档属性
| 名称 | 北师大版八年级数学下册第3章 图形的平移与旋转 检测题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 855.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-01 10:10:29 | ||
图片预览

文档简介
北师大版八下第3章 图形的平移与旋转 检测题
一、选择题(共10小题)
1. 下列图形中,能将其中一个图形平移得到另一个图形的是
A. B.
C. D.
2. 如图,紫荆花图案绕中心至少旋转 后能与原来的图案互相重合,则 的值为
A. B. C. D.
3. 下列图案是一些汽车的车标,可以看作由“基本图案”平移得到的是
A. B.
C. D.
4. 如图,若要使这个图案与自身重合,则至少绕它的中心旋转
A. B. C. D.
5. 如图,线段 经过平移得到线段 其中点 , 的对应点分别为点 ,,这四个点都在格点上.若线段 上有一个点 则点 在 上的对应点 的坐标为
A. B.
C. D.
6. 如图,已知 是 绕点 逆时针旋转所得,其中点 在射线 上,设旋转角为 ,直线 与直线 交于点 ,那么下列结论不正确的是
A. B. C. D.
7. 不等式组 的整数解共有
A. 个 B. 个 C. 个 D. 个
8. 如图,将 绕点 逆时针旋转 ,得到 ,若点 在线段 的延长线上,则 的大小为
A. B. C. D.
9. 如图,在 中,,将 绕点 顺时针旋转得到 ,使点 的对应点 恰好落在边 上,点 的对应点为 ,延长 交 于点 ,则下列结论一定正确的是
A. B. C. D.
10. 如图,在平面直角坐标系中,点 的坐标为 , 沿 轴向右平移后得到 ,点 的对应点 在直线 上,则点 与其对应点 间的距离为
A. B. C. D.
二、填空题(共8小题)
11. 如图, 和 关于点 中心对称,则 绕点 转了 度到达 ,且 .
12. 如图,直径为 的圆 平移 到圆 的位置,则图中阴影部分的面积为 .
13. 如图所示,在方格纸上建立的平面直角坐标系中,如果将 绕点 按顺时针方向旋转 ,得到 ,那么点 的对应点 的坐标是 .
14. 一副三角板如图放置,将三角板 绕点 逆时针旋转 (),使得三角板 的一边所在的直线与 垂直,则 的度数为 .
15. 在直角坐标平面内,点 向下平移 个单位后,所得的点的坐标是 .
16. 如图,在 中,,将 绕点 顺时针旋转 ,得到 ,连接 ,若 ,,则线段 的长为 .
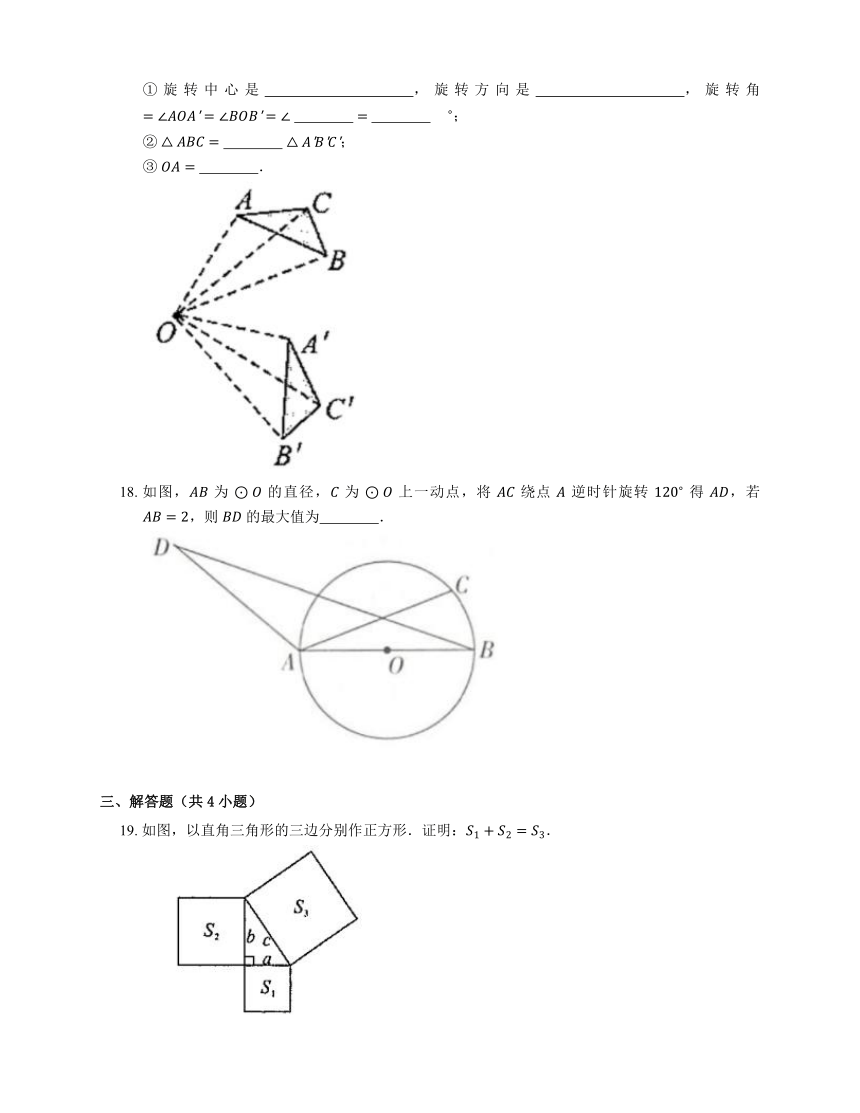
17. 如图, 绕点 旋转 到 ,则:
①旋转中心是 ,旋转方向是 ,旋转角 ;
② ;
③ .
18. 如图, 为 的直径, 为 上一动点,将 绕点 逆时针旋转 得 ,若 ,则 的最大值为 .
三、解答题(共4小题)
19. 如图,以直角三角形的三边分别作正方形.证明:.
20. 如图所示, 是边长为 的等边三角形,,,, 分别在边 , 上,且 ,求 的周长.
21. 如图,在四边形 中, 与 相交于点 , 为 上一点,且 ,.
(1)说明 与 全等的理由;
(2)说明 与 全等的理由.
22. 如图,在正方形 中,, 是对角线 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,求证:
(1) 是 的平分线;
(2).
答案
1. A 【解析】A、图形的形状和大小没有变化,符合平移的性质,属于平移得到;
B、图形由轴对称得到,不属于平移得到,不属于平移得到;
C、图形由旋转变换得到,不符合平移的性质,不属于平移得到;
D、图形的大小发生变化,不属于平移得到.
2. D
3. C
【解析】A、可以由一个“基本图案”旋转得到,不可以由一个“基本图案”平移得到,故本选项错误;
B、是轴对称图形,不是基本图案的组合图形,故本选项错误;
C、可以由一个“基本图案”平移得到,故把本选项正确;
D、不可以由一个“基本图案”平移得到,故把本选项错误.
4. A
5. A
【解析】本题考查图形的平移.由图形可知点 的坐标为 ,点 的坐标为 , 点 可看作点 先向左平移 个单位,再问上平移 个单位得到的, 点 的坐标为 ,点 的坐标为 .
6. D
【解析】 是由 旋转得到,
,,
,
,
故A,B,C正确.
7. C
8. D
【解析】连接 ,
将 绕点 逆时针旋转 ,得到 ,
,,,
,
.
9. D
【解析】由旋转的性质得 ,,,,
故A,B,C中结论不一定正确.
中,,
又 ,
,
,
.
10. C
【解析】如图,连接 ,,
点 的坐标为 , 沿 轴向右平移后得到 ,
点 的纵坐标是 .
又 点 的对应点 在直线 上,
,解得 ,
根据平移的性质知 ,
故选C.
11. ,
12.
13.
14. 或
15.
16.
【解析】由旋转的性质可知 ,,.
在 中,,,,由勾股定理得 .
.
在 中,,即 的长为 .
17. 点,顺时针,,,,
18.
【解析】如图,将 绕点 顺时针旋转 得 ,则 ,易知当 ,, 三点共线时、 最大,即 最大,
过 作 交 的延长线于点 ,
,,
,
中,,
,,
由勾股定理得 ,
,故 的最大值为 .
19. 由题知 ,,,
又 ,
.
20. 延长 至点 ,使 ,连接 .
是等边三角形,
.
,,
.
.
.
在 和 中,
,.,
.
,.
,,
.
.
在 和 中,
,,,
.
.
.
.
21. (1) 因为 (已知),
又因为 (邻补角的意义),
所以 (等式性质).
在 和 中,
所以 .
(2) 因为 ,
所以 (全等三角形对应边相等),(全等三角形对应角相等),
在 与 中,
所以 .
22. (1) 将 绕点 顺吋针旋转 后,得到 ,
,,,
,
,
,
.
在 和 中,
,
,
是 的平分线..
(2) 由()得 ,
,
由旋转知 ,
又 ,
,即 .
在 中,,
则 .
一、选择题(共10小题)
1. 下列图形中,能将其中一个图形平移得到另一个图形的是
A. B.
C. D.
2. 如图,紫荆花图案绕中心至少旋转 后能与原来的图案互相重合,则 的值为
A. B. C. D.
3. 下列图案是一些汽车的车标,可以看作由“基本图案”平移得到的是
A. B.
C. D.
4. 如图,若要使这个图案与自身重合,则至少绕它的中心旋转
A. B. C. D.
5. 如图,线段 经过平移得到线段 其中点 , 的对应点分别为点 ,,这四个点都在格点上.若线段 上有一个点 则点 在 上的对应点 的坐标为
A. B.
C. D.
6. 如图,已知 是 绕点 逆时针旋转所得,其中点 在射线 上,设旋转角为 ,直线 与直线 交于点 ,那么下列结论不正确的是
A. B. C. D.
7. 不等式组 的整数解共有
A. 个 B. 个 C. 个 D. 个
8. 如图,将 绕点 逆时针旋转 ,得到 ,若点 在线段 的延长线上,则 的大小为
A. B. C. D.
9. 如图,在 中,,将 绕点 顺时针旋转得到 ,使点 的对应点 恰好落在边 上,点 的对应点为 ,延长 交 于点 ,则下列结论一定正确的是
A. B. C. D.
10. 如图,在平面直角坐标系中,点 的坐标为 , 沿 轴向右平移后得到 ,点 的对应点 在直线 上,则点 与其对应点 间的距离为
A. B. C. D.
二、填空题(共8小题)
11. 如图, 和 关于点 中心对称,则 绕点 转了 度到达 ,且 .
12. 如图,直径为 的圆 平移 到圆 的位置,则图中阴影部分的面积为 .
13. 如图所示,在方格纸上建立的平面直角坐标系中,如果将 绕点 按顺时针方向旋转 ,得到 ,那么点 的对应点 的坐标是 .
14. 一副三角板如图放置,将三角板 绕点 逆时针旋转 (),使得三角板 的一边所在的直线与 垂直,则 的度数为 .
15. 在直角坐标平面内,点 向下平移 个单位后,所得的点的坐标是 .
16. 如图,在 中,,将 绕点 顺时针旋转 ,得到 ,连接 ,若 ,,则线段 的长为 .
17. 如图, 绕点 旋转 到 ,则:
①旋转中心是 ,旋转方向是 ,旋转角 ;
② ;
③ .
18. 如图, 为 的直径, 为 上一动点,将 绕点 逆时针旋转 得 ,若 ,则 的最大值为 .
三、解答题(共4小题)
19. 如图,以直角三角形的三边分别作正方形.证明:.
20. 如图所示, 是边长为 的等边三角形,,,, 分别在边 , 上,且 ,求 的周长.
21. 如图,在四边形 中, 与 相交于点 , 为 上一点,且 ,.
(1)说明 与 全等的理由;
(2)说明 与 全等的理由.
22. 如图,在正方形 中,, 是对角线 上两点,且 ,将 绕点 顺时针旋转 后,得到 ,连接 ,求证:
(1) 是 的平分线;
(2).
答案
1. A 【解析】A、图形的形状和大小没有变化,符合平移的性质,属于平移得到;
B、图形由轴对称得到,不属于平移得到,不属于平移得到;
C、图形由旋转变换得到,不符合平移的性质,不属于平移得到;
D、图形的大小发生变化,不属于平移得到.
2. D
3. C
【解析】A、可以由一个“基本图案”旋转得到,不可以由一个“基本图案”平移得到,故本选项错误;
B、是轴对称图形,不是基本图案的组合图形,故本选项错误;
C、可以由一个“基本图案”平移得到,故把本选项正确;
D、不可以由一个“基本图案”平移得到,故把本选项错误.
4. A
5. A
【解析】本题考查图形的平移.由图形可知点 的坐标为 ,点 的坐标为 , 点 可看作点 先向左平移 个单位,再问上平移 个单位得到的, 点 的坐标为 ,点 的坐标为 .
6. D
【解析】 是由 旋转得到,
,,
,
,
故A,B,C正确.
7. C
8. D
【解析】连接 ,
将 绕点 逆时针旋转 ,得到 ,
,,,
,
.
9. D
【解析】由旋转的性质得 ,,,,
故A,B,C中结论不一定正确.
中,,
又 ,
,
,
.
10. C
【解析】如图,连接 ,,
点 的坐标为 , 沿 轴向右平移后得到 ,
点 的纵坐标是 .
又 点 的对应点 在直线 上,
,解得 ,
根据平移的性质知 ,
故选C.
11. ,
12.
13.
14. 或
15.
16.
【解析】由旋转的性质可知 ,,.
在 中,,,,由勾股定理得 .
.
在 中,,即 的长为 .
17. 点,顺时针,,,,
18.
【解析】如图,将 绕点 顺时针旋转 得 ,则 ,易知当 ,, 三点共线时、 最大,即 最大,
过 作 交 的延长线于点 ,
,,
,
中,,
,,
由勾股定理得 ,
,故 的最大值为 .
19. 由题知 ,,,
又 ,
.
20. 延长 至点 ,使 ,连接 .
是等边三角形,
.
,,
.
.
.
在 和 中,
,.,
.
,.
,,
.
.
在 和 中,
,,,
.
.
.
.
21. (1) 因为 (已知),
又因为 (邻补角的意义),
所以 (等式性质).
在 和 中,
所以 .
(2) 因为 ,
所以 (全等三角形对应边相等),(全等三角形对应角相等),
在 与 中,
所以 .
22. (1) 将 绕点 顺吋针旋转 后,得到 ,
,,,
,
,
,
.
在 和 中,
,
,
是 的平分线..
(2) 由()得 ,
,
由旋转知 ,
又 ,
,即 .
在 中,,
则 .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
