2.2.3 二次函数y=a(x-h)2和y=a(x-h)2+k的图象与性质 课件(共28张PPT)
文档属性
| 名称 | 2.2.3 二次函数y=a(x-h)2和y=a(x-h)2+k的图象与性质 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-01 20:18:14 | ||
图片预览



文档简介
(共28张PPT)
2.2.3 二次函数y=a(x-h)2和y=a(x-h)2+k的图象与性质
北师大版 九年级 下册
教学目标
教学目标:1.利用描点法画出二次函数y=a图象.
2.理解抛物线y=a与抛物线y=ax2的相互关系.
3.掌握抛物线y=a与抛物线y=ax2的平移规律.
教学重点:通过图象,观察抛物线y=a的图象和性质.
教学难点:通过图象,观察抛物线y=a与抛物线y=ax2的平移规律.
新知讲解
合作学习
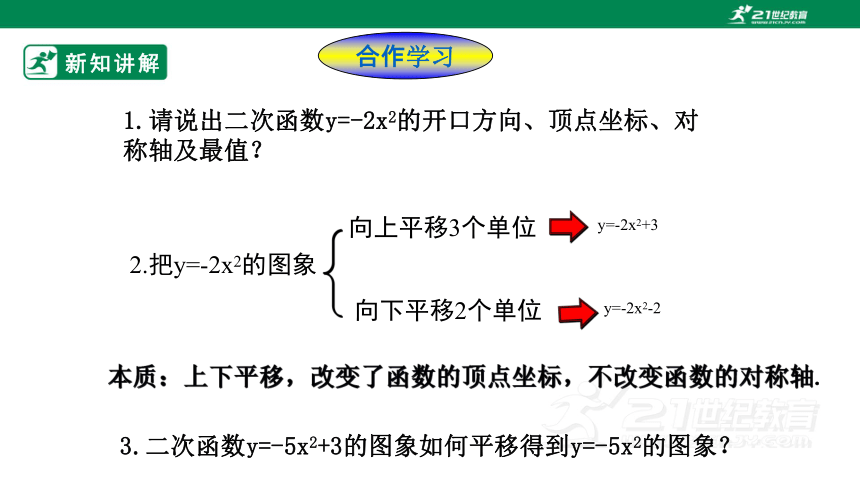
1.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值?
2.把y=-2x2的图象
向上平移3个单位
y=-2x2+3
向下平移2个单位
y=-2x2-2
3.二次函数y=-5x2+3的图象如何平移得到y=-5x2的图象?
本质:上下平移,改变了函数的顶点坐标,不改变函数的对称轴.
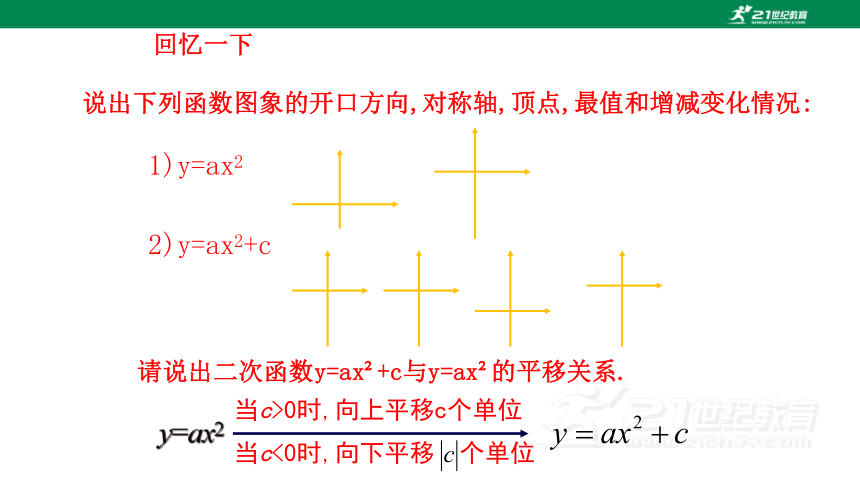
说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
1)y=ax2
2)y=ax2+c
请说出二次函数y=ax +c与y=ax 的平移关系.
y=ax2
当c>0时,向上平移c个单位
当c<0时,向下平移 个单位
回忆一下
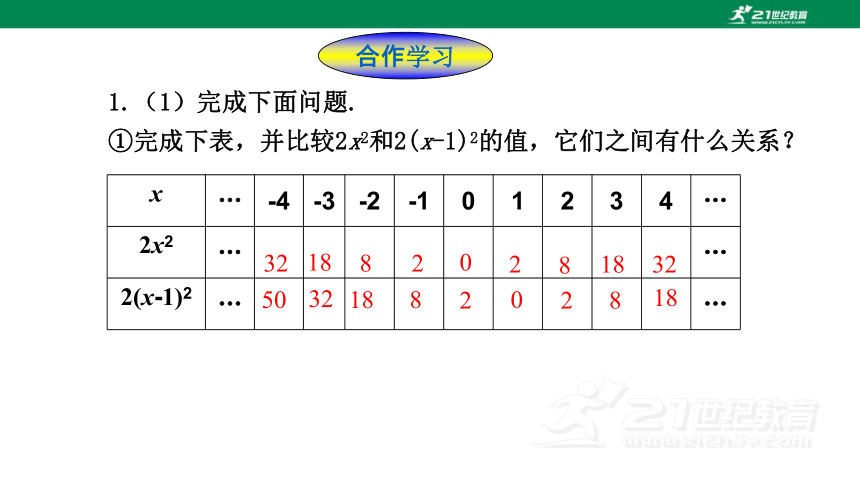
1.(1)完成下面问题.
①完成下表,并比较2x2和2(x-1)2的值,它们之间有什么关系?
x … -4 -3 -2 -1 0 1 2 3 4 …
2x2 … …
2(x-1)2 … …
32
18
8
2
0
2
8
18
32
50
32
18
8
2
0
2
8
18
合作学习
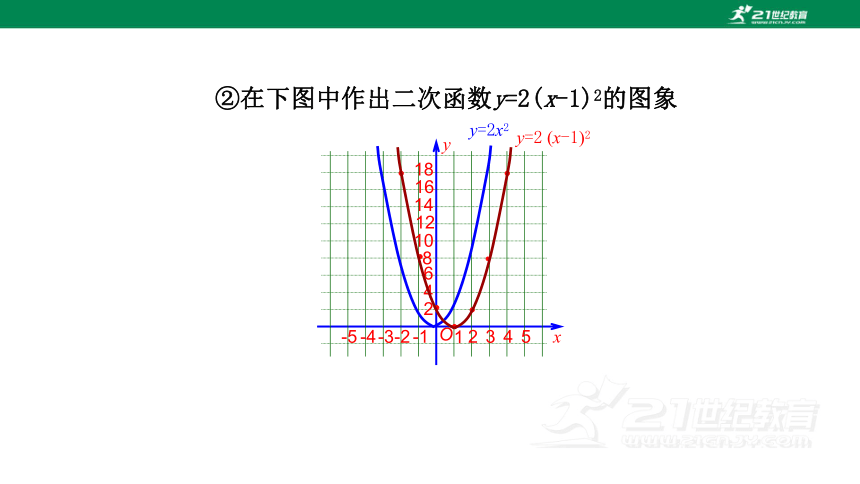
②在下图中作出二次函数y=2(x-1)2的图象
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
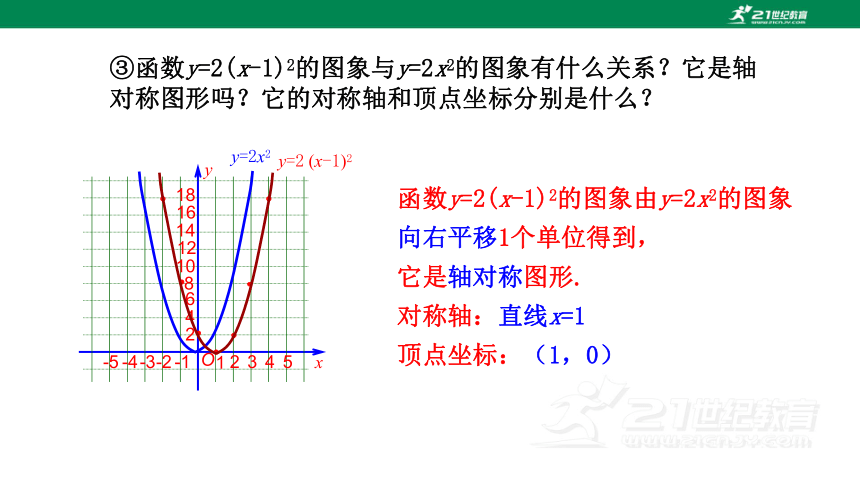
③函数y=2(x-1)2的图象与y=2x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
函数y=2(x-1)2的图象由y=2x2的图象
向右平移1个单位得到,
它是轴对称图形.
对称轴:直线x=1
顶点坐标:(1,0)
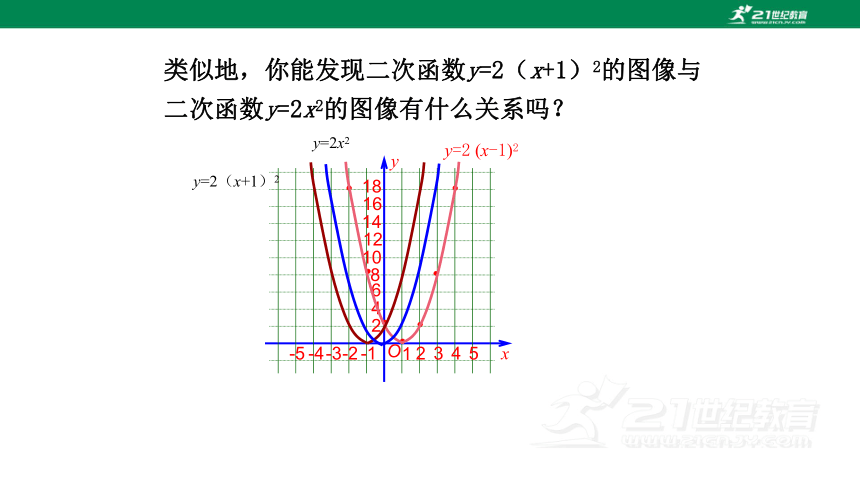
类似地,你能发现二次函数y=2(x+1)2的图像与二次函数y=2x2的图像有什么关系吗?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
y=2(x+1)2
探索与思考
-2
2
-2
-4
-6
4
-4
y
x
0
向左平移一个单位
向右平移一个单位
向右平移2个单位
向左平移2个单位
提炼概念
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
本质:左右平移,改变了函数的对称轴位置,
不改变函数的最值。
括号内左加右减;括号外不变.
④对于函数y=2(x-1)2和y=2(x+1)2,x取哪些值时, y值随x值的增大而增大? x取哪些值时, y值随x值的增大而减小?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
y=2(x+1)2
函数y=2(x-1)2(y=2x2或y=2(x+1)2)
当x>1 (x>0 或 x>-1)时,
y值随x值的增大而增大;
当x<1 (x<0 或 x<-1)时,
y值随x值的增大而减小.
基础函数y=2x2的所有与范围和位置有关的性质全部作对应的平移即可得到平移函数的对应的性质.
二次函数 y=a(x-h)2的性质
y=a(x-h)2 a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,0)
(h,0)
当x=h时,y最小值=0
当x=h时,y最大值=0
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
o
y
x
画出二次函数y=3(x-1)2+2的图象,并与二次函数y=3x2的图象进行比较,说明它们之间的关系.
探究二
函数 的图象
函数 的图象
函数 的图象
函数 的图象
向右
平移
1个
单位
向上平移
2个单位
向右
平移
1个
单位
向上平移
2个单位
的图象
向右平移h个
单位
的图象
向右平移h个
单位
的图象
向上平移 k 个
单位
的图象
向上平移 k 个
单位
对称轴:直线x= h
顶点: (h,k)
【规律方法】
(当k,h都大于0时)的图象特点.
典例精讲
例.将抛物线y=2(x+1)2-3向右平移1个单位长度,再向上平移3个单位长度,则所得抛物线的表达式为_____________.
答案:y=2x2
归纳概念
二次函数y=a(x-h)2+k的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂练习
1.抛物线y=4x2抛物线的相同点是( )
A.顶点相同 B.对称轴相同
C.开口方向相同 D.顶点都在x轴上
【详解】
解:抛物线y=4x2的开口向上,对称轴为y轴,顶点为(0,0),
抛物线y= 4(x+2)2的开口向下,对称轴为直线x= 2,顶点是( 2,0),
∴抛物线y=4x2与抛物线y= 4(x+2)2的相同点是顶点都在x轴上,
故选:D.
D
A
4.已知A(,y1),B(1,y2),C(4,y3)三点都在二次函数
y=﹣(x﹣2)2的图象上,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2
C.y3<y1<y2 D.y3<y2<y1
【详解】解:二次函数y=﹣(x﹣2)2的图象开口向下,对称轴为x=2,在对称轴左侧,y随x的增大而增大∴C(4,y3)关于对称轴的对称点为(0,y3),∵﹣<0<1<2,∴y1<y3<y2,
故选:B.
5.抛物线y=3(x-2)2的开口方向是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
【详解】
解:抛物线y=3(x-2)2的开口方向是向上,顶点坐标为(2,0),对称轴是直线x= 2.当x≥2时,y随x的增大而增大;当x=2时,y有最小值是0,它可以由抛物线y=3x2向右平移2个单位得到.
6.已知抛物线y=a(x-2)2+1与x轴有两个交点,把该抛物线向下平移m个单位长度得到新抛物线与x轴没有交点,则m的值可以是___________.(只填一个符合题意的值即可)
【答案】2(答案不唯一)
【分析】先根据抛物线y=a(x-2)2+1与x轴有两个交点,得出a<0,然后写出平移后的抛物线解析式为y=a(x-2)2+1-m,根据新抛物线与x轴没有交点,得出1-m<0,再求解即可.
7.在直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)当-3解 (1)∵二次函数的图象的顶点为A(1,-4),
当1∴0=a(3-1)2-4,∴a=1,∴y=(x-1)2-4.
∴该二次函数为y=a(x-1)2-4.
∵该二次函数的图象过点B(3,0),
(2)∵y=(x-1)2-4,
∴其对称轴是直线x=1,
∴当-3课堂总结
课堂总结
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.2.3 二次函数y=a(x-h)2和y=a(x-h)2+k的图象与性质
北师大版 九年级 下册
教学目标
教学目标:1.利用描点法画出二次函数y=a图象.
2.理解抛物线y=a与抛物线y=ax2的相互关系.
3.掌握抛物线y=a与抛物线y=ax2的平移规律.
教学重点:通过图象,观察抛物线y=a的图象和性质.
教学难点:通过图象,观察抛物线y=a与抛物线y=ax2的平移规律.
新知讲解
合作学习
1.请说出二次函数y=-2x2的开口方向、顶点坐标、对称轴及最值?
2.把y=-2x2的图象
向上平移3个单位
y=-2x2+3
向下平移2个单位
y=-2x2-2
3.二次函数y=-5x2+3的图象如何平移得到y=-5x2的图象?
本质:上下平移,改变了函数的顶点坐标,不改变函数的对称轴.
说出下列函数图象的开口方向,对称轴,顶点,最值和增减变化情况:
1)y=ax2
2)y=ax2+c
请说出二次函数y=ax +c与y=ax 的平移关系.
y=ax2
当c>0时,向上平移c个单位
当c<0时,向下平移 个单位
回忆一下
1.(1)完成下面问题.
①完成下表,并比较2x2和2(x-1)2的值,它们之间有什么关系?
x … -4 -3 -2 -1 0 1 2 3 4 …
2x2 … …
2(x-1)2 … …
32
18
8
2
0
2
8
18
32
50
32
18
8
2
0
2
8
18
合作学习
②在下图中作出二次函数y=2(x-1)2的图象
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
③函数y=2(x-1)2的图象与y=2x2的图象有什么关系?它是轴对称图形吗?它的对称轴和顶点坐标分别是什么?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
函数y=2(x-1)2的图象由y=2x2的图象
向右平移1个单位得到,
它是轴对称图形.
对称轴:直线x=1
顶点坐标:(1,0)
类似地,你能发现二次函数y=2(x+1)2的图像与二次函数y=2x2的图像有什么关系吗?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
y=2(x+1)2
探索与思考
-2
2
-2
-4
-6
4
-4
y
x
0
向左平移一个单位
向右平移一个单位
向右平移2个单位
向左平移2个单位
提炼概念
二次函数y=a(x-h)2的图象与y=ax2 的图象的关系
可以看作互相平移得到(h>0).
左右平移规律:
y=a(x-h)2
当向左平移 ︱h︱ 时
y=a(x+h)2
当向右平移 ︱h︱ 时
y=ax2
本质:左右平移,改变了函数的对称轴位置,
不改变函数的最值。
括号内左加右减;括号外不变.
④对于函数y=2(x-1)2和y=2(x+1)2,x取哪些值时, y值随x值的增大而增大? x取哪些值时, y值随x值的增大而减小?
1
2
3
4
5
x
2
4
6
8
10
12
14
16
18
y
O
-1
-2
-3
-4
-5
y=2 (x-1)2
y=2x2
y=2(x+1)2
函数y=2(x-1)2(y=2x2或y=2(x+1)2)
当x>1 (x>0 或 x>-1)时,
y值随x值的增大而增大;
当x<1 (x<0 或 x<-1)时,
y值随x值的增大而减小.
基础函数y=2x2的所有与范围和位置有关的性质全部作对应的平移即可得到平移函数的对应的性质.
二次函数 y=a(x-h)2的性质
y=a(x-h)2 a>0 a<0
开口方向
对称轴
顶点坐标
最值
增减性
要点归纳
向上
向下
直线x=h
直线x=h
(h,0)
(h,0)
当x=h时,y最小值=0
当x=h时,y最大值=0
当x<h时,y随x的增大而减小;x>h时,y随x的增大而增大.
当x>h时,y随x的增大而减小;x<h时,y随x的增大而增大.
o
y
x
画出二次函数y=3(x-1)2+2的图象,并与二次函数y=3x2的图象进行比较,说明它们之间的关系.
探究二
函数 的图象
函数 的图象
函数 的图象
函数 的图象
向右
平移
1个
单位
向上平移
2个单位
向右
平移
1个
单位
向上平移
2个单位
的图象
向右平移h个
单位
的图象
向右平移h个
单位
的图象
向上平移 k 个
单位
的图象
向上平移 k 个
单位
对称轴:直线x= h
顶点: (h,k)
【规律方法】
(当k,h都大于0时)的图象特点.
典例精讲
例.将抛物线y=2(x+1)2-3向右平移1个单位长度,再向上平移3个单位长度,则所得抛物线的表达式为_____________.
答案:y=2x2
归纳概念
二次函数y=a(x-h)2+k的图象和性质
抛物线
顶点坐标
对称轴
开口方向
增减性
最值
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
(h,k)
(h,k)
直线x=h
直线x=h
向上
向下
当x=h时,最小值为k.
当x=h时,最大值为k.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
课堂练习
1.抛物线y=4x2抛物线的相同点是( )
A.顶点相同 B.对称轴相同
C.开口方向相同 D.顶点都在x轴上
【详解】
解:抛物线y=4x2的开口向上,对称轴为y轴,顶点为(0,0),
抛物线y= 4(x+2)2的开口向下,对称轴为直线x= 2,顶点是( 2,0),
∴抛物线y=4x2与抛物线y= 4(x+2)2的相同点是顶点都在x轴上,
故选:D.
D
A
4.已知A(,y1),B(1,y2),C(4,y3)三点都在二次函数
y=﹣(x﹣2)2的图象上,则y1,y2,y3的大小关系为( )
A.y1<y2<y3 B.y1<y3<y2
C.y3<y1<y2 D.y3<y2<y1
【详解】解:二次函数y=﹣(x﹣2)2的图象开口向下,对称轴为x=2,在对称轴左侧,y随x的增大而增大∴C(4,y3)关于对称轴的对称点为(0,y3),∵﹣<0<1<2,∴y1<y3<y2,
故选:B.
5.抛物线y=3(x-2)2的开口方向是______,顶点坐标为______,对称轴是______.当x______时,y随x的增大而增大;当x=______时,y有最______值是______,它可以由抛物线y=3x2向______平移______个单位得到.
【详解】
解:抛物线y=3(x-2)2的开口方向是向上,顶点坐标为(2,0),对称轴是直线x= 2.当x≥2时,y随x的增大而增大;当x=2时,y有最小值是0,它可以由抛物线y=3x2向右平移2个单位得到.
6.已知抛物线y=a(x-2)2+1与x轴有两个交点,把该抛物线向下平移m个单位长度得到新抛物线与x轴没有交点,则m的值可以是___________.(只填一个符合题意的值即可)
【答案】2(答案不唯一)
【分析】先根据抛物线y=a(x-2)2+1与x轴有两个交点,得出a<0,然后写出平移后的抛物线解析式为y=a(x-2)2+1-m,根据新抛物线与x轴没有交点,得出1-m<0,再求解即可.
7.在直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)当-3
当1
∴该二次函数为y=a(x-1)2-4.
∵该二次函数的图象过点B(3,0),
(2)∵y=(x-1)2-4,
∴其对称轴是直线x=1,
∴当-3
课堂总结
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
