北师大版九年级上册数学 2.3.2一元二次方程的根的判别式 课件(共18张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 2.3.2一元二次方程的根的判别式 课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 793.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 20:44:56 | ||
图片预览




文档简介
(共18张PPT)
一元二次方程根的判别式
1. 感悟一元二次方程根的判别式的产生的过程,体会模型思想
2. 能运用根的判别式,判别方程根的情况和进行有关的推理论证
3. 会运用根的判别式求一元二次方程中字母系数的取值范围
4. 培养学生的探索、创新精神, 加深师生间的交流,增进师生的情感,培养学生的协作精神
学习目标
环节
1
学习内容
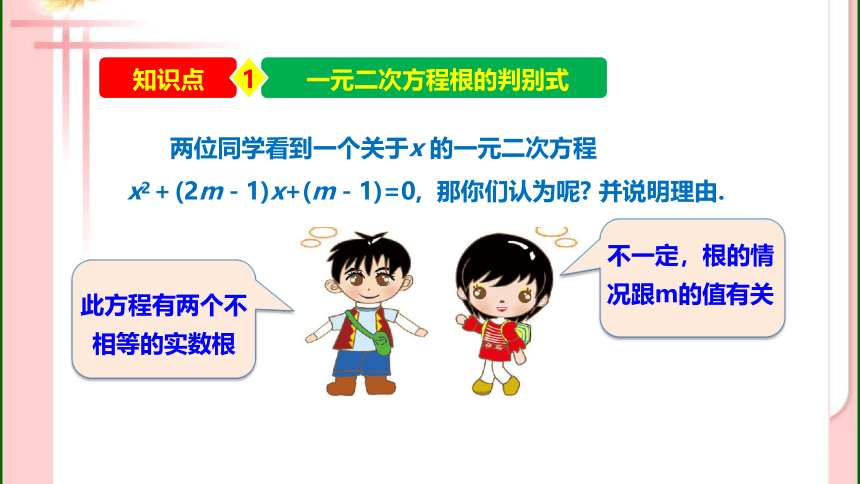
两位同学看到一个关于x 的一元二次方程
x2+(2m-1)x+(m-1)=0, 那你们认为呢 并说明理由.
此方程有两个不相等的实数根
不一定,根的情况跟m的值有关
知识点
1
一元二次方程根的判别式
请一位同学利用配方法求出一元二次方程ax2+bx+c=0(a不为0)的根
课前热身
探索一元二次方程根的判别式
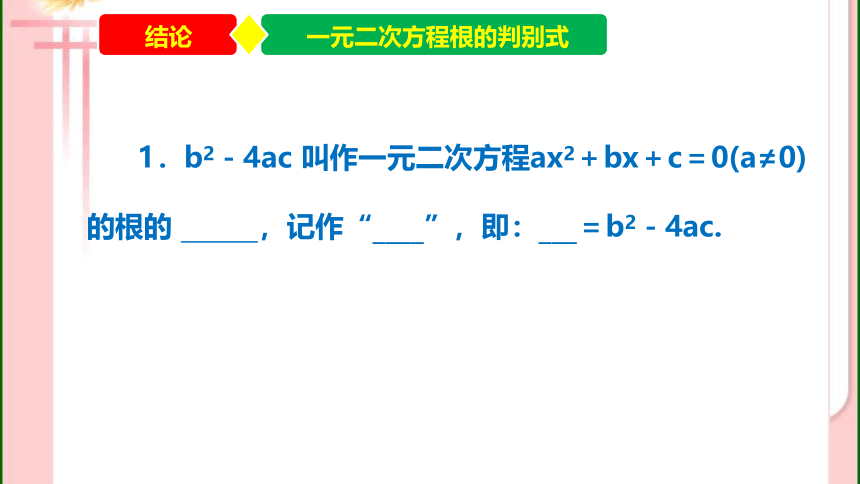
1.b2-4ac 叫作一元二次方程ax2+bx+c=0(a≠0)的根的 ,记作“____”,即:___=b2-4ac.
结论
一元二次方程根的判别式
2. 一元二次方程ax2+bx+c=0(a≠0)的根的情况可由Δ=b2-4ac 来判断:
知识点
2
一元二次方程根的判别式的类别
方程4x2+x=5化为一般形式ax2+bx+c=0后,a,b,c 的值为( )
小练习
1
一元二次方程根的判别式
求一元二次方程的根的判别式时应注意两点:
一是将方程化成一般形式后才能确定a,b,c 的值;
二是确定a,b,c 的值时不要漏掉符号.
课堂小结
1
一元二次方程根的判别式
下面各数值是某个一元二次方程根的判别式的值,其中能使该方程有两个不相等的实数根的有:
知识点
3
一元二次方程根的判别式的应用
a、c异号
b=0且a、c同号
b、c均为0
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
知识点
3
一元二次方程根的判别式的应用
连线题将对应项用直线连起来
不解方程,判别下列方程根的情况:
(1) x2+3x+2=0;
(2) x2-4x+4=0;
(3) 2x2-4x+5=0.
知识点
3
一元二次方程根的判别式的应用
若b<0,关于x的一元二次方程(x-1)2=b的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.不确定
知识点
3
一元二次方程根的判别式的应用
已知关于x的方程x2+x+m=0有两个不相等的实数根,则m的最大整数值是______.
知识点
3
一元二次方程根的判别式的应用
关于x的一元二次方程(a+1)x2-4x-1=0有两个不相等的实数根,求a的取值范围。
知识点
3
一元二次方程根的判别式的应用
两位同学看到一个关于x 的一元二次方程
x2+(2m-1)x+(m-1)=0, 那你们认为呢 并说明理由.
此方程有两个不相等的实数根
不一定,根的情况跟m的值有关
回头看
一元二次方程根的判别式的应用
一元二次方程根的判别式的应用:
1. 直用:不解方程,判断方程根的情况
2. 逆用:由方程根的情况,求字母系数的取值范围
注意:一元二次方程有实数根,包含有两个相等的实数根和有两个不相等的实数根两种情况
课堂总结
一元二次方程根的判别式
课堂总结
一元二次方程根的判别式
一元二次方程根的判别式
1. 感悟一元二次方程根的判别式的产生的过程,体会模型思想
2. 能运用根的判别式,判别方程根的情况和进行有关的推理论证
3. 会运用根的判别式求一元二次方程中字母系数的取值范围
4. 培养学生的探索、创新精神, 加深师生间的交流,增进师生的情感,培养学生的协作精神
学习目标
环节
1
学习内容
两位同学看到一个关于x 的一元二次方程
x2+(2m-1)x+(m-1)=0, 那你们认为呢 并说明理由.
此方程有两个不相等的实数根
不一定,根的情况跟m的值有关
知识点
1
一元二次方程根的判别式
请一位同学利用配方法求出一元二次方程ax2+bx+c=0(a不为0)的根
课前热身
探索一元二次方程根的判别式
1.b2-4ac 叫作一元二次方程ax2+bx+c=0(a≠0)的根的 ,记作“____”,即:___=b2-4ac.
结论
一元二次方程根的判别式
2. 一元二次方程ax2+bx+c=0(a≠0)的根的情况可由Δ=b2-4ac 来判断:
知识点
2
一元二次方程根的判别式的类别
方程4x2+x=5化为一般形式ax2+bx+c=0后,a,b,c 的值为( )
小练习
1
一元二次方程根的判别式
求一元二次方程的根的判别式时应注意两点:
一是将方程化成一般形式后才能确定a,b,c 的值;
二是确定a,b,c 的值时不要漏掉符号.
课堂小结
1
一元二次方程根的判别式
下面各数值是某个一元二次方程根的判别式的值,其中能使该方程有两个不相等的实数根的有:
知识点
3
一元二次方程根的判别式的应用
a、c异号
b=0且a、c同号
b、c均为0
方程有两个不相等的实数根
方程有两个相等的实数根
方程没有实数根
知识点
3
一元二次方程根的判别式的应用
连线题将对应项用直线连起来
不解方程,判别下列方程根的情况:
(1) x2+3x+2=0;
(2) x2-4x+4=0;
(3) 2x2-4x+5=0.
知识点
3
一元二次方程根的判别式的应用
若b<0,关于x的一元二次方程(x-1)2=b的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.不确定
知识点
3
一元二次方程根的判别式的应用
已知关于x的方程x2+x+m=0有两个不相等的实数根,则m的最大整数值是______.
知识点
3
一元二次方程根的判别式的应用
关于x的一元二次方程(a+1)x2-4x-1=0有两个不相等的实数根,求a的取值范围。
知识点
3
一元二次方程根的判别式的应用
两位同学看到一个关于x 的一元二次方程
x2+(2m-1)x+(m-1)=0, 那你们认为呢 并说明理由.
此方程有两个不相等的实数根
不一定,根的情况跟m的值有关
回头看
一元二次方程根的判别式的应用
一元二次方程根的判别式的应用:
1. 直用:不解方程,判断方程根的情况
2. 逆用:由方程根的情况,求字母系数的取值范围
注意:一元二次方程有实数根,包含有两个相等的实数根和有两个不相等的实数根两种情况
课堂总结
一元二次方程根的判别式
课堂总结
一元二次方程根的判别式
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
