北师大版九年级上册数学 2.6.2建立一元二次方程解决销售问题 课件(共14张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 2.6.2建立一元二次方程解决销售问题 课件(共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 20:45:46 | ||
图片预览




文档简介
(共14张PPT)
2.6 应用一元二次方程
解决几何问题
为迎接本年度的赛马活动,我县准备在赛马场附近开辟一块面积为600平方米的长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少米
情境引入
2.如图,在这块长30 m,宽20 m的长方形绿地上修建同样宽的两条垂直小路, 使得剩余绿地面积和为504 m2,则小路的宽应为多少?
30
20
(面积问题)
解:设小路宽为 m,则绿地的长 m,宽 m,由题意得:
答:小路宽应为2米。
合作交流一
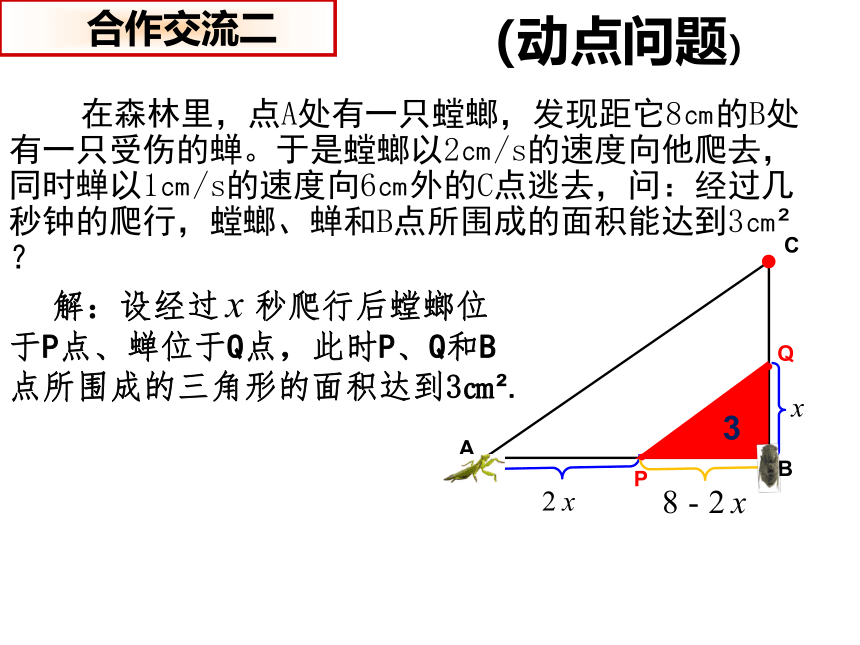
在森林里,点A处有一只螳螂,发现距它8㎝的B处有一只受伤的蝉。于是螳螂以2㎝/s的速度向他爬去,同时蝉以1㎝/s的速度向6㎝外的C点逃去,问:经过几秒钟的爬行,螳螂、蝉和B点所围成的面积能达到3㎝ ?
C
A
B
P
Q
3
合作交流二
解:设经过 秒爬行后螳螂位于P点、蝉位于Q点,此时P、Q和B点所围成的三角形的面积达到3㎝ .
(动点问题)
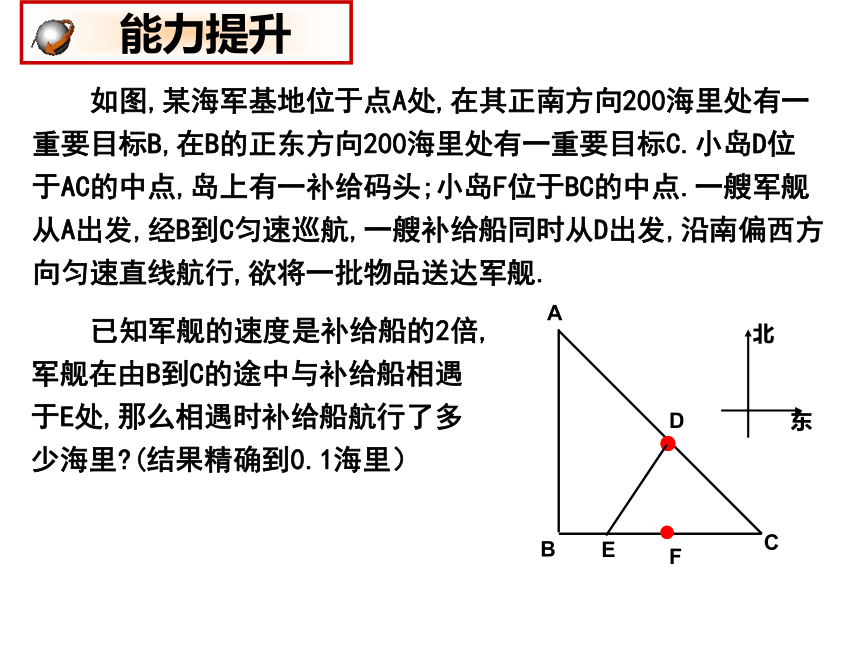
如图,某海军基地位于点A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
能力提升
A
B
D
C
E
F
北
东
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里)
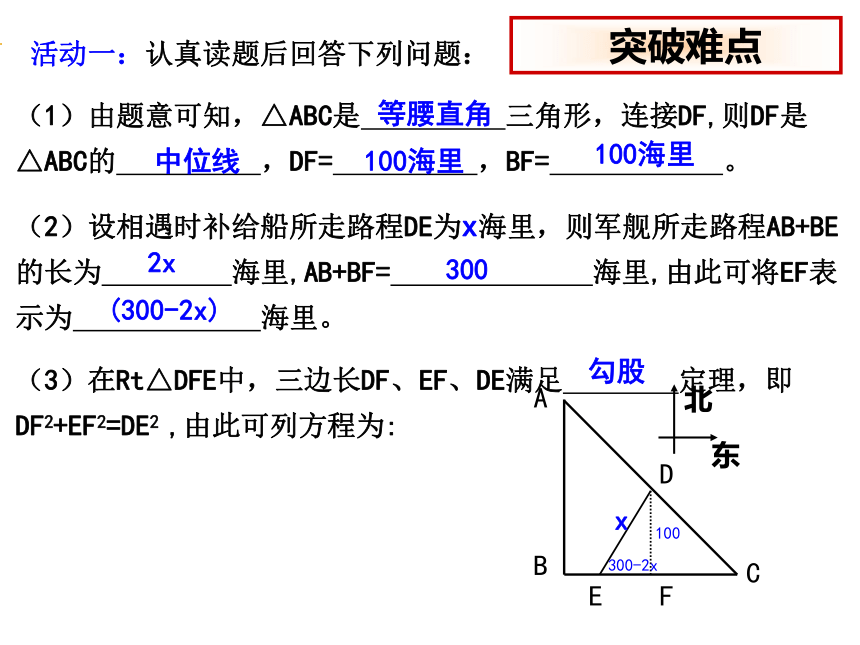
活动一:认真读题后回答下列问题:
(1)由题意可知,△ABC是 三角形,连接DF,则DF是△ABC的 ,DF= ,BF= 。
(2)设相遇时补给船所走路程DE为x海里,则军舰所走路程AB+BE的长为 海里,AB+BF= 海里,由此可将EF表示为 海里。
(3)在Rt△DFE中,三边长DF、EF、DE满足 定理,即DF2+EF2=DE2 ,由此可列方程为:
北
东
A
B
C
D
E
F
2x
勾股
中位线
100海里
等腰直角
100海里
300
300-2x
x
100
(300-2x)
突破难点
解题过程
A
北
东
B
D
C
E
F
图 2-8
x
100
若设相遇时补给船的行程DE为x海里
连接DF.
∵AD=CD,BF=CF
∴DF是 ABC的中位线
∴DF∥AB,且DF= AB
∵AB⊥BC,AB=BC=200海里
∵DF⊥BC,DF=100海里,BF=100海里
∴EF=AB+BF-(AB+BE)=(300- 2x)海里 。
在Rt DEF中,根据勾股定理可得方程:
整理,得:
(舍去)
所以,相遇是补给船大约航行了118.4海里
解:
那么 DE= 海里,AB+BE= 海里
x
2x
应用方程解决实际问题的一般步骤:
知识点小结
审
设
列
解
验
答
关键:寻找等量关系
思想方法: 方程思想 转化思想
数形结合思想
如图,在Rt△ABC中,∠C=90°, AC=30cm, BC=25cm, 动点P从点C出发,沿CA方向运动,速度是2cm/s;同时,动点Q从B出发,沿BC方向运动,速度是1cm/s,几秒后P、Q两点相距25cm
解:设x秒后,P、Q两点相距25cm.
在Rt△CPQ中,由勾股定理得
答:10秒后,P、Q两点相距25cm。
A
Q
P
C
B
学以致用
课堂小结
本节课选取了一些几何和现实生活中的题材,让同学们经历列一元二次方程解决问题的过程.当我们在建构方程数学模型,刻画现实世界、解决实际问题时,应注意哪些重要环节
整体地、系统地审清问题
把握问题中的等量关系,列出方程
正确求解方程并检验解的合理性
谈谈这节课你收获了什么
备选习题2
备选习题1
建立数学模型
突破难点
A
B
D
C
E
F
北
东
200
A
100
分析:
200
V军=2V补
T军=T补
300
BF=100 海里
能力提升
C
B
A
5 ?
D
E
在上述问题中,螳螂、蝉和B点围成的三角形面积能达到5㎝ 吗?若能,请求出爬行时间;若不能,请说明理由。
解:设经过 秒爬行后螳螂位于D点、蝉位于E点,此时D、E和B点所围成的三角形的面积达到5㎝ .
返回
在螳螂和蝉的问题中,请问:在爬行过程中何时它们三个围成的面积最大,最大值是多少?
能力拓展
C
B
A
最大
D
E
返回
2.6 应用一元二次方程
解决几何问题
为迎接本年度的赛马活动,我县准备在赛马场附近开辟一块面积为600平方米的长方形绿地,并且长比宽多10米,那么绿地的长和宽各为多少米
情境引入
2.如图,在这块长30 m,宽20 m的长方形绿地上修建同样宽的两条垂直小路, 使得剩余绿地面积和为504 m2,则小路的宽应为多少?
30
20
(面积问题)
解:设小路宽为 m,则绿地的长 m,宽 m,由题意得:
答:小路宽应为2米。
合作交流一
在森林里,点A处有一只螳螂,发现距它8㎝的B处有一只受伤的蝉。于是螳螂以2㎝/s的速度向他爬去,同时蝉以1㎝/s的速度向6㎝外的C点逃去,问:经过几秒钟的爬行,螳螂、蝉和B点所围成的面积能达到3㎝ ?
C
A
B
P
Q
3
合作交流二
解:设经过 秒爬行后螳螂位于P点、蝉位于Q点,此时P、Q和B点所围成的三角形的面积达到3㎝ .
(动点问题)
如图,某海军基地位于点A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C.小岛D位于AC的中点,岛上有一补给码头;小岛F位于BC的中点.一艘军舰从A出发,经B到C匀速巡航,一艘补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
能力提升
A
B
D
C
E
F
北
东
已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里 (结果精确到0.1海里)
活动一:认真读题后回答下列问题:
(1)由题意可知,△ABC是 三角形,连接DF,则DF是△ABC的 ,DF= ,BF= 。
(2)设相遇时补给船所走路程DE为x海里,则军舰所走路程AB+BE的长为 海里,AB+BF= 海里,由此可将EF表示为 海里。
(3)在Rt△DFE中,三边长DF、EF、DE满足 定理,即DF2+EF2=DE2 ,由此可列方程为:
北
东
A
B
C
D
E
F
2x
勾股
中位线
100海里
等腰直角
100海里
300
300-2x
x
100
(300-2x)
突破难点
解题过程
A
北
东
B
D
C
E
F
图 2-8
x
100
若设相遇时补给船的行程DE为x海里
连接DF.
∵AD=CD,BF=CF
∴DF是 ABC的中位线
∴DF∥AB,且DF= AB
∵AB⊥BC,AB=BC=200海里
∵DF⊥BC,DF=100海里,BF=100海里
∴EF=AB+BF-(AB+BE)=(300- 2x)海里 。
在Rt DEF中,根据勾股定理可得方程:
整理,得:
(舍去)
所以,相遇是补给船大约航行了118.4海里
解:
那么 DE= 海里,AB+BE= 海里
x
2x
应用方程解决实际问题的一般步骤:
知识点小结
审
设
列
解
验
答
关键:寻找等量关系
思想方法: 方程思想 转化思想
数形结合思想
如图,在Rt△ABC中,∠C=90°, AC=30cm, BC=25cm, 动点P从点C出发,沿CA方向运动,速度是2cm/s;同时,动点Q从B出发,沿BC方向运动,速度是1cm/s,几秒后P、Q两点相距25cm
解:设x秒后,P、Q两点相距25cm.
在Rt△CPQ中,由勾股定理得
答:10秒后,P、Q两点相距25cm。
A
Q
P
C
B
学以致用
课堂小结
本节课选取了一些几何和现实生活中的题材,让同学们经历列一元二次方程解决问题的过程.当我们在建构方程数学模型,刻画现实世界、解决实际问题时,应注意哪些重要环节
整体地、系统地审清问题
把握问题中的等量关系,列出方程
正确求解方程并检验解的合理性
谈谈这节课你收获了什么
备选习题2
备选习题1
建立数学模型
突破难点
A
B
D
C
E
F
北
东
200
A
100
分析:
200
V军=2V补
T军=T补
300
BF=100 海里
能力提升
C
B
A
5 ?
D
E
在上述问题中,螳螂、蝉和B点围成的三角形面积能达到5㎝ 吗?若能,请求出爬行时间;若不能,请说明理由。
解:设经过 秒爬行后螳螂位于D点、蝉位于E点,此时D、E和B点所围成的三角形的面积达到5㎝ .
返回
在螳螂和蝉的问题中,请问:在爬行过程中何时它们三个围成的面积最大,最大值是多少?
能力拓展
C
B
A
最大
D
E
返回
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
