北师大版九年级上册数学 3.2用频率估计概率 课件(共17张PPT)
文档属性
| 名称 | 北师大版九年级上册数学 3.2用频率估计概率 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 20:46:40 | ||
图片预览





文档简介
(共17张PPT)
用频率估计概率
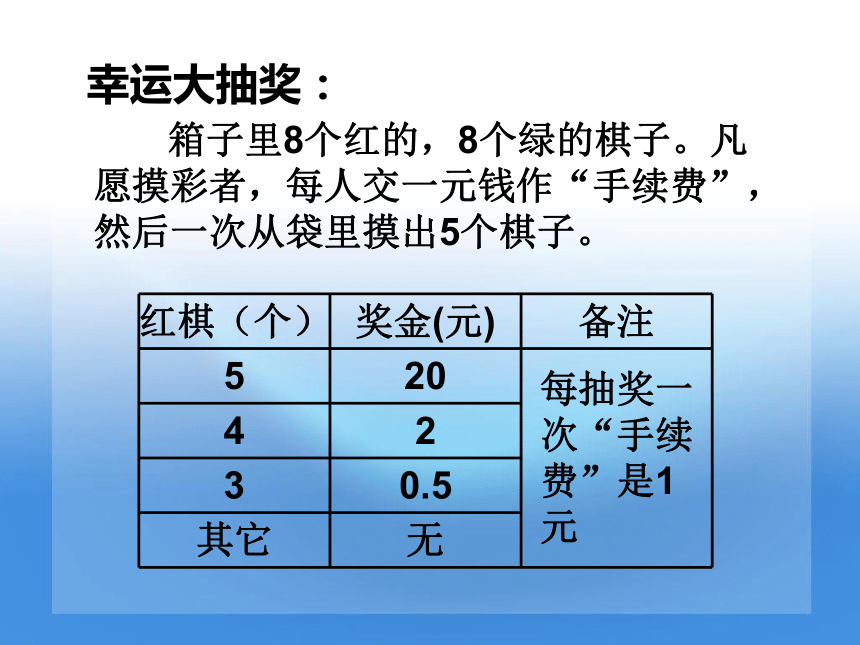
幸运大抽奖:
箱子里8个红的,8个绿的棋子。凡愿摸彩者,每人交一元钱作“手续费”,然后一次从袋里摸出5个棋子。
红棋(个) 奖金(元) 备注
5 20 每抽奖一次“手续费”是1元
4 2
3 0.5
其它 无
次数 红棋 奖金 次数 红棋 奖金
5 20 6
4 2 7
3 0.5 8
其它 无 9
1 10
2 11
3 12
4 13
5 14
随机现象:在一定条件下,具有多种可能的
结果,而事先又不能确定会出现
哪种结果。
随机事件:在一定条件下,可能发生也可能
不发生的事件(用A,B,C …表示)
必然事件:在一定条件下,必然发生的事件
不可能事件:在一定条件下,不可能发生的
事件(用“ ”表示 )。
(用“Ω”表示 )。
例1 设有8个红子8个绿子的“抽奖”中,
A={随机摸出5个棋子,有3个红子};
B={随机摸出10个棋子,有9个红子};
C={随机摸出10个棋子,有红子};
解:依题可知,A是随机事件;
B是不可能事件;
C是必然事件。
例题讲解
(1)掷一颗骰子,记录掷出的点数。
(2)掷一枚硬币,出现正面。
(3)一天某一时刻,某个人的体温。
(4)如果2x-4=0,那么,x=2。
(5)手电筒的电池没电,灯泡发亮。
巩固练习:
1、指出下列事件是必然事件,不可能事件,还是随机事件。
(6)江门地区2011年6月1日会下雨。
(7)幸运大抽奖摸中五颗红棋子。
(随机事件)
(必然事件)
(不可能事件)
(随机事件)
(随机事件)
(随机事件)
(随机事件)
2、请同学们说说我们日常生活遇到的随机事件、必然事件、不可能事件。
数学实验:
将一枚硬币抛掷10 次或更多,观察正面出现的次数。
次数 正/反 次数 正/反
1 7
2 8
3 9
4 10
5 ……
6
根据实验分别回答下列问题:
(1)在实验中出现了几种实验结果?还有其它实验结果吗?
(2)这些实验结果正面出现的频数是多少?正面出现的频率是多少?
(3)如果允许你做大量重复试验,你认为正面出现的概率是多少?
设在n次重复试验中,事件A发生了m次(0≤m≤n ),m叫事件A发生的频数,事件A的频数在试验的总次数中所占的比例 叫做事件A发生的频率。
一般地,当试验次数充分大时,事件A发生的频率 总在某个常数附近摆动,就把这个常数叫做事件A发生的概率,记作P(A) 。
概率:Probability
构建概念
实验者
德.摩根
蒲丰
K.皮尔逊
K.皮尔逊
2048
1061
0.5181
4040
2048
0.5069
12000
6019
0.5016
24000
12012
0.5005
这种试验历史上曾有不少统计学家做过
0.5
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做
7 遍, 观察正面出现的次数及频率.
试验
序号
1 2 3 4 5 6 7
2
3
1 5 1 2 4
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, m/n值呈现出稳定性
m
m
m
例2:将一枚硬币抛掷10 次,观察正面出现的次数为4次,正面出现频数是多少?正面出现的频率是多少?
解:依题可知n=10,m=4
则正面出现的频数是4
频率= = = 0.4
则正面出现的频率是0.4
任何事件的概率都在0-1之间,必然事件的概率为1,不可能事件的概率为0,随机事件的概率为0≤P(A)≤1。
(3)对任一事件A, P(A)= ,因为0≤m≤n,
所以0≤P(A)≤1;
概率的性质
(1)对于必然事件Ω ,P(Ω)=1;
(2)对于不可能事件 ,P( )=0;
例3、某种新药在使用的患者中进行调查的结果如下表:
调查患者
人数(n) 100 200 500 1000 2000
用药有效
人数(m) 85 180 435 884 1761
有效频率 ( )
请填写表中有效频率一栏,并指出该药的有效概率是多少?(答案: )
0.85
0.90
0. 87
0. 884
0. 8805
0.88
按摸1000次统计,应用概率知识,可知
摸到5个白棋子的概率约为0.0128;
摸到4个白棋子的概率约为0.1282;
摸到3个白棋子的概率约为0.359。
按照1000次摸彩来计算:
收入:1000元;
支出:20×13+128×2+0.5×359=695.5(元)
即每1000次摸彩,可赚300元以上。
游戏大揭秘:
例:12个同类产品中有10个正品,2个次品,从12个产品中任意抽出3个
(1)3个都是正品的事件是________事件.
(2)至少有一个次品的事件是_______ 事件.
(3)3个都是次品的事件是__________事件.
(4)恰有1个正品的事件是__________事件.
(5)至少1个正品的事件是__________事件.
(随机)
(不可能)
(随机)
(必然)
(随机)
用频率估计概率
幸运大抽奖:
箱子里8个红的,8个绿的棋子。凡愿摸彩者,每人交一元钱作“手续费”,然后一次从袋里摸出5个棋子。
红棋(个) 奖金(元) 备注
5 20 每抽奖一次“手续费”是1元
4 2
3 0.5
其它 无
次数 红棋 奖金 次数 红棋 奖金
5 20 6
4 2 7
3 0.5 8
其它 无 9
1 10
2 11
3 12
4 13
5 14
随机现象:在一定条件下,具有多种可能的
结果,而事先又不能确定会出现
哪种结果。
随机事件:在一定条件下,可能发生也可能
不发生的事件(用A,B,C …表示)
必然事件:在一定条件下,必然发生的事件
不可能事件:在一定条件下,不可能发生的
事件(用“ ”表示 )。
(用“Ω”表示 )。
例1 设有8个红子8个绿子的“抽奖”中,
A={随机摸出5个棋子,有3个红子};
B={随机摸出10个棋子,有9个红子};
C={随机摸出10个棋子,有红子};
解:依题可知,A是随机事件;
B是不可能事件;
C是必然事件。
例题讲解
(1)掷一颗骰子,记录掷出的点数。
(2)掷一枚硬币,出现正面。
(3)一天某一时刻,某个人的体温。
(4)如果2x-4=0,那么,x=2。
(5)手电筒的电池没电,灯泡发亮。
巩固练习:
1、指出下列事件是必然事件,不可能事件,还是随机事件。
(6)江门地区2011年6月1日会下雨。
(7)幸运大抽奖摸中五颗红棋子。
(随机事件)
(必然事件)
(不可能事件)
(随机事件)
(随机事件)
(随机事件)
(随机事件)
2、请同学们说说我们日常生活遇到的随机事件、必然事件、不可能事件。
数学实验:
将一枚硬币抛掷10 次或更多,观察正面出现的次数。
次数 正/反 次数 正/反
1 7
2 8
3 9
4 10
5 ……
6
根据实验分别回答下列问题:
(1)在实验中出现了几种实验结果?还有其它实验结果吗?
(2)这些实验结果正面出现的频数是多少?正面出现的频率是多少?
(3)如果允许你做大量重复试验,你认为正面出现的概率是多少?
设在n次重复试验中,事件A发生了m次(0≤m≤n ),m叫事件A发生的频数,事件A的频数在试验的总次数中所占的比例 叫做事件A发生的频率。
一般地,当试验次数充分大时,事件A发生的频率 总在某个常数附近摆动,就把这个常数叫做事件A发生的概率,记作P(A) 。
概率:Probability
构建概念
实验者
德.摩根
蒲丰
K.皮尔逊
K.皮尔逊
2048
1061
0.5181
4040
2048
0.5069
12000
6019
0.5016
24000
12012
0.5005
这种试验历史上曾有不少统计学家做过
0.5
实例 将一枚硬币抛掷 5 次、50 次、500 次, 各做
7 遍, 观察正面出现的次数及频率.
试验
序号
1 2 3 4 5 6 7
2
3
1 5 1 2 4
22
25
21
25
24
18
27
251
249
256
247
251
262
258
0.4
0.6
0.2
1.0
0.2
0.4
0.8
0.44
0.50
0.42
0.48
0.36
0.54
0.502
0.498
0.512
0.494
0.524
0.516
0.50
0.502
波动最小
随n的增大, m/n值呈现出稳定性
m
m
m
例2:将一枚硬币抛掷10 次,观察正面出现的次数为4次,正面出现频数是多少?正面出现的频率是多少?
解:依题可知n=10,m=4
则正面出现的频数是4
频率= = = 0.4
则正面出现的频率是0.4
任何事件的概率都在0-1之间,必然事件的概率为1,不可能事件的概率为0,随机事件的概率为0≤P(A)≤1。
(3)对任一事件A, P(A)= ,因为0≤m≤n,
所以0≤P(A)≤1;
概率的性质
(1)对于必然事件Ω ,P(Ω)=1;
(2)对于不可能事件 ,P( )=0;
例3、某种新药在使用的患者中进行调查的结果如下表:
调查患者
人数(n) 100 200 500 1000 2000
用药有效
人数(m) 85 180 435 884 1761
有效频率 ( )
请填写表中有效频率一栏,并指出该药的有效概率是多少?(答案: )
0.85
0.90
0. 87
0. 884
0. 8805
0.88
按摸1000次统计,应用概率知识,可知
摸到5个白棋子的概率约为0.0128;
摸到4个白棋子的概率约为0.1282;
摸到3个白棋子的概率约为0.359。
按照1000次摸彩来计算:
收入:1000元;
支出:20×13+128×2+0.5×359=695.5(元)
即每1000次摸彩,可赚300元以上。
游戏大揭秘:
例:12个同类产品中有10个正品,2个次品,从12个产品中任意抽出3个
(1)3个都是正品的事件是________事件.
(2)至少有一个次品的事件是_______ 事件.
(3)3个都是次品的事件是__________事件.
(4)恰有1个正品的事件是__________事件.
(5)至少1个正品的事件是__________事件.
(随机)
(不可能)
(随机)
(必然)
(随机)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
