5.3.1平行线的性质 精品课件(共27张PPT)
文档属性
| 名称 | 5.3.1平行线的性质 精品课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第五章
相交线与平行线
5.3.1平行线的性质
教学目标/Teaching aims
1
掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;
2
能够根据平行线的性质进行简单的推理.
复习回顾
平行线的判定方法
简单可以说成:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
判定方法1:
同位角相等,两条直线平行。
复习回顾
平行线的判定方法
简单可以说成:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
判定方法2:
内错角相等,两条直线平行。
复习回顾
简单可以说成:
两条直线被第三条直线所截,如果同旁内角,那么这两条直线平行。
判定方法3:
同旁内角互补,两条直线平行。
平行线的判定方法
新课导入
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
新知探究
平行线的性质
活动 如图5.3-1画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
如图5.3-1
新知探究
平行线的性质
∠1、∠2……中哪些是同位角?
思考:
∠1与∠5、∠2与∠6、∠3与∠7、∠4与∠8
它们的度数之间有什么数量关系?
∠1=∠5、∠2=∠6、∠3=∠7、∠4=∠8
你发现了什么?
两条平行线被第三条直线所截,同位角相等。
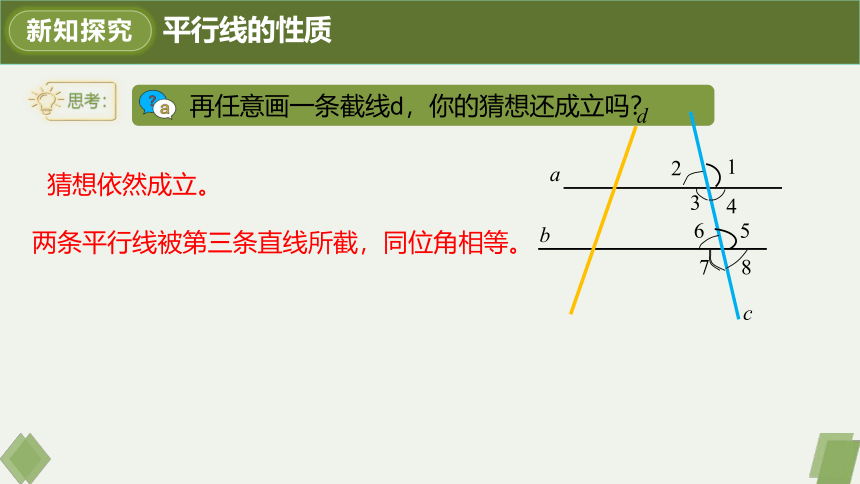
再任意画一条截线d,你的猜想还成立吗?
新知探究
平行线的性质
b
1
2
a
c
5
6
7
8
3
4
d
思考:
猜想依然成立。
两条平行线被第三条直线所截,同位角相等。
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,同位角相等。
性质1:
两直线平行,同位角相等。
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
b
1
2
a
c
新知探究
平行线的性质
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
新知探究
平行线的性质
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,内错角相等。
性质2:
两直线平行,内错角相等。
应用格式:
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
b
1
2
a
c
3
新知探究
平行线的性质
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2
(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角的性质),
∴ 2+ 4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,同旁内角互补。
性质3:
两直线平行,同旁内角互补。
应用格式:
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
巩固练习
1.如图,直线AB、CD被直线EF所截,AB∥CD,∠1=110°,则∠2
等于( )
A.65° B.70° C.75° D.80°
B
巩固练习
2.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3
的度数为( )
A.110° B.115° C.120° D.130°
A
巩固练习
3.已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,
并在括号内注明理由.
(1)∵DE∥AB,( )
∴∠2=______.(_____________,_____________)
(2)∵DE∥AB,( )
∴∠3=______.(_______________,_________________)
(3)∵DE∥AB( )
∴∠1+______=180°.(________________,________________)
已知
∠5
两直线平行
内错角相等
已知
∠B
两直线平行
同位角相等
已知
∠2
两直线平行
同旁内角互补
巩固练习
4.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,
且∠1=∠2=30°,∠3=84°,求∠4的度数.
解:∵CD⊥AB,FE⊥AB,
∴∠BEF=∠BDC=90°,
∴FE∥CD,
∴∠2=∠BCD,
∵∠1=∠2=30°,
∴∠1=∠BCD=30°,
∴DG∥BC,
∴∠3=∠ACB=∠4+∠BCD,
∴∠4=84°﹣30°=54°.
课堂练习
1.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40 ° B.50° C.70° D.80°
C
课堂练习
2.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30 ° B.60° C.80° D.120°
A
课堂练习
3.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
4.如图,已知AB∥CD,∠1=130°,则∠2= .
50°
课堂练习
5.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A、G、H、D,且∠1=∠2,∠B=∠C,求证:∠A=∠D.
证明:∵∠1=∠2,
∴CE∥BF,
∴∠B=∠AEC,
又∵∠B=∠C,
∴∠AEC=∠C,
∴AB∥CD,
∴∠A=∠D.
课堂练习
6.如图,一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°,第二次拐弯时∠C是多少度?为什么?
解:∠C=142°.
两直线平行,内错角相等.
B
C
课堂练习
思维拓展:如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
课堂总结
平行线的性质
性质1:
两直线平行,同位角相等。
性质2:
两直线平行,内错角相等。
性质3:
两直线平行,同旁内角互补。
5.3.1平行线的性质
谢谢观看
相交线与平行线
第五章
相交线与平行线
5.3.1平行线的性质
教学目标/Teaching aims
1
掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补;
2
能够根据平行线的性质进行简单的推理.
复习回顾
平行线的判定方法
简单可以说成:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
判定方法1:
同位角相等,两条直线平行。
复习回顾
平行线的判定方法
简单可以说成:
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
判定方法2:
内错角相等,两条直线平行。
复习回顾
简单可以说成:
两条直线被第三条直线所截,如果同旁内角,那么这两条直线平行。
判定方法3:
同旁内角互补,两条直线平行。
平行线的判定方法
新课导入
思考 反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
新知探究
平行线的性质
活动 如图5.3-1画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
如图5.3-1
新知探究
平行线的性质
∠1、∠2……中哪些是同位角?
思考:
∠1与∠5、∠2与∠6、∠3与∠7、∠4与∠8
它们的度数之间有什么数量关系?
∠1=∠5、∠2=∠6、∠3=∠7、∠4=∠8
你发现了什么?
两条平行线被第三条直线所截,同位角相等。
再任意画一条截线d,你的猜想还成立吗?
新知探究
平行线的性质
b
1
2
a
c
5
6
7
8
3
4
d
思考:
猜想依然成立。
两条平行线被第三条直线所截,同位角相等。
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,同位角相等。
性质1:
两直线平行,同位角相等。
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
b
1
2
a
c
新知探究
平行线的性质
思考:在上一节中,我们利用“同位角相等,两直线平行线”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等, 能否得到内错角之间的数量关系?
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
新知探究
平行线的性质
解 ∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,内错角相等。
性质2:
两直线平行,内错角相等。
应用格式:
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
b
1
2
a
c
3
新知探究
平行线的性质
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2
(两直线平行,同位角相等).
∵ 1+ 4=180°
(邻补角的性质),
∴ 2+ 4=180°
(等量代换).
思考:类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
归纳小结
平行线的性质
平行线的性质
简单可以说成:
两条平行线被第三条直线所截,同旁内角互补。
性质3:
两直线平行,同旁内角互补。
应用格式:
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补)
∵a∥b(已知)
巩固练习
1.如图,直线AB、CD被直线EF所截,AB∥CD,∠1=110°,则∠2
等于( )
A.65° B.70° C.75° D.80°
B
巩固练习
2.如图,直线a、b被c所截,若a∥b,∠1=45°,∠2=65°,则∠3
的度数为( )
A.110° B.115° C.120° D.130°
A
巩固练习
3.已知:如图,DE∥AB.请根据已知条件进行推理,分别得出结论,
并在括号内注明理由.
(1)∵DE∥AB,( )
∴∠2=______.(_____________,_____________)
(2)∵DE∥AB,( )
∴∠3=______.(_______________,_________________)
(3)∵DE∥AB( )
∴∠1+______=180°.(________________,________________)
已知
∠5
两直线平行
内错角相等
已知
∠B
两直线平行
同位角相等
已知
∠2
两直线平行
同旁内角互补
巩固练习
4.如图,已知CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,
且∠1=∠2=30°,∠3=84°,求∠4的度数.
解:∵CD⊥AB,FE⊥AB,
∴∠BEF=∠BDC=90°,
∴FE∥CD,
∴∠2=∠BCD,
∵∠1=∠2=30°,
∴∠1=∠BCD=30°,
∴DG∥BC,
∴∠3=∠ACB=∠4+∠BCD,
∴∠4=84°﹣30°=54°.
课堂练习
1.如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
A.40 ° B.50° C.70° D.80°
C
课堂练习
2.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C为( )
A.30 ° B.60° C.80° D.120°
A
课堂练习
3.如图,直线AB,CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3= 80 度.
4.如图,已知AB∥CD,∠1=130°,则∠2= .
50°
课堂练习
5.如图,一条直线分别与直线BE、直线CE、直线BF、直线CF相交于点A、G、H、D,且∠1=∠2,∠B=∠C,求证:∠A=∠D.
证明:∵∠1=∠2,
∴CE∥BF,
∴∠B=∠AEC,
又∵∠B=∠C,
∴∠AEC=∠C,
∴AB∥CD,
∴∠A=∠D.
课堂练习
6.如图,一条公路两次拐弯的前后两条路互相平行.第一次拐弯时∠B是142°,第二次拐弯时∠C是多少度?为什么?
解:∠C=142°.
两直线平行,内错角相等.
B
C
课堂练习
思维拓展:如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?
解:∠2=∠3.
两直线行,内错角相等;
∵∠1=∠2=∠3=∠4,
∴ ∠5=∠6,
∴进入潜望镜的光线和
离开潜望镜的光线平行.
课堂总结
平行线的性质
性质1:
两直线平行,同位角相等。
性质2:
两直线平行,内错角相等。
性质3:
两直线平行,同旁内角互补。
5.3.1平行线的性质
谢谢观看
相交线与平行线
