6.1平方根 第2课时 精品课件(共20张PPT)
文档属性
| 名称 | 6.1平方根 第2课时 精品课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第6.1平方根第2课时
人教版数学七年级下册
学习目标
1.会用计算器求一个数的算术平方根.
2.能用夹值法求一个数的算术平方根的近似值.
3.理解无限不循环小数的概念.
复习引入
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
0的算术平方根是 .
算术平方根:
中的双重非负性:
a≥0
0
互动新授
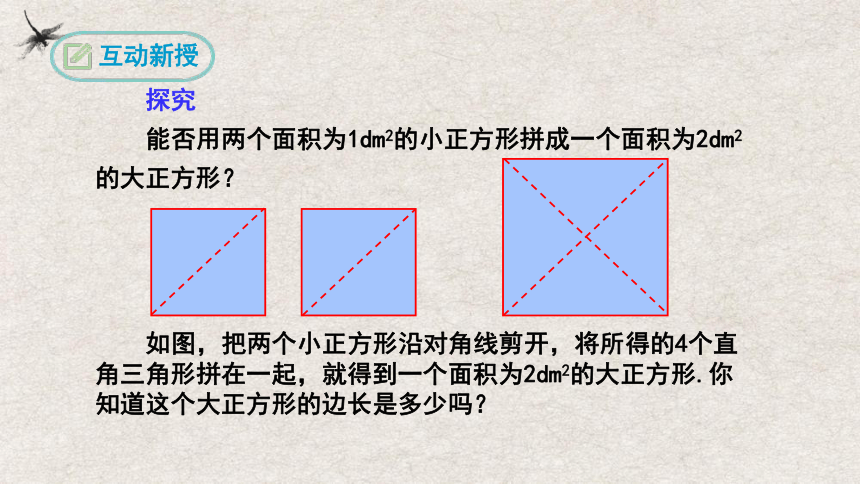
探究
能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2dm2的大正方形.你知道这个大正方形的边长是多少吗?
互动新授
解: 设大正方形的边长为xdm,则
由算术平方根的定义可知
所以大正方形的边长是 dm.
探究
有多大呢?
互动新授
∵12=1,22=4,
∴1< <2;
∵1.42=1.96,1.52=2.25,
∴1.4< <1.5;
∵1.412=1.9881,1.422=2.0164,
∴1.41< <1.42;
∵1.4142=1.999396,1.4152=2.002225,
∴114< <1.415;
.......
互动新授
如此下去,可以得到 的更精确的近似值.事实上
=1.414 213 562 373……,它是一个无限不循环小数.
实际上,许多正有理数的算术平方根(例如 , ,
等)都是无限不循环小数.
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根(或其近视值).
互动新授
例2 用计算器求下列各式的值:
解:(1)依次按键 3136 ,
显示:56.
∴
(2)依次按键 2 ,
显示:1.414213562.
∴
=
=
… …
… …
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
探究 (1)利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
互动新授
2
1
2
1
探究(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出,, 的近似值,你能根据 的值说出是多少吗?
不能
互动新授
典例精析
例3 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3∶2. 她不知能否裁得出来,正在发愁. 小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?
400cm2
300cm2
解:
设长方形的长为3xcm,则宽为2xcm.
∴长方形纸片的长为
∴小丽不能裁出符合要求的纸片.
典例精析
∵ ,
∴正方形纸片的边长只有20cm,
1.估算13的算术平方根在( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
2.面积为19m2的正方形,它的边长介于( )
A.2m与3m之间 B.3m与4m之间
C.4m与5m之间 D.5m与6m之间
C
小试牛刀
1.估计的值在( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
2.已知:≈44.91,=14.0,则的值约为( )
A.32.41 B.1.40
C.3.241 D.4.491
C
D
课堂检测
4.若已知,,那么 .
3.若那么
.
11.18
0.3535
74500
课堂检测
1.比较大小:与0.5.
解:∵ 7>4,
∴
∴,
∴ 0.5 .
拓展训练
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
算术平方根的规律
无限不循环小数
被开方数的小数点向右每移动2位,它的算术平方根的小数点就向右移动1位;
被开方数的小数点向左每移动2位,它的算术平方根的小数点就向左移动1位.
课堂小结
1.设n为正整数,且,则n的值为( )
A.5 B.6 C.7 D.8
D
2.若2<<3,则a的值可以是( )
A.﹣7 B. C. D.12
C
课后作业
3.设n为正整数,且n<A.5 B.6 C.7 D.8
4.与最接近的整数是 ( )
A.7 B.8 C.9 D.10
C
C
课后作业
谢谢聆听
第6.1平方根第2课时
人教版数学七年级下册
学习目标
1.会用计算器求一个数的算术平方根.
2.能用夹值法求一个数的算术平方根的近似值.
3.理解无限不循环小数的概念.
复习引入
一般地,如一个正数x的平方等于a,即x2=a ,那么这个正数x就叫做a的算术平方根.
0的算术平方根是 .
算术平方根:
中的双重非负性:
a≥0
0
互动新授
探究
能否用两个面积为1dm2的小正方形拼成一个面积为2dm2的大正方形?
如图,把两个小正方形沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2dm2的大正方形.你知道这个大正方形的边长是多少吗?
互动新授
解: 设大正方形的边长为xdm,则
由算术平方根的定义可知
所以大正方形的边长是 dm.
探究
有多大呢?
互动新授
∵12=1,22=4,
∴1< <2;
∵1.42=1.96,1.52=2.25,
∴1.4< <1.5;
∵1.412=1.9881,1.422=2.0164,
∴1.41< <1.42;
∵1.4142=1.999396,1.4152=2.002225,
∴114< <1.415;
.......
互动新授
如此下去,可以得到 的更精确的近似值.事实上
=1.414 213 562 373……,它是一个无限不循环小数.
实际上,许多正有理数的算术平方根(例如 , ,
等)都是无限不循环小数.
大多数计算器都有 键,用它可以求出一个正有理数的算术平方根(或其近视值).
互动新授
例2 用计算器求下列各式的值:
解:(1)依次按键 3136 ,
显示:56.
∴
(2)依次按键 2 ,
显示:1.414213562.
∴
=
=
… …
… …
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
探究 (1)利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
互动新授
2
1
2
1
探究(2)用计算器计算 (精确到0.001),并利用你在(1)中发现的规律说出,, 的近似值,你能根据 的值说出是多少吗?
不能
互动新授
典例精析
例3 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3∶2. 她不知能否裁得出来,正在发愁. 小明见了说“别发愁,一定能用一块面积大的纸片裁出一块面积小的纸片”,你同意小明的说法吗? 小丽能用这块纸片裁出符合要求的纸片吗?
400cm2
300cm2
解:
设长方形的长为3xcm,则宽为2xcm.
∴长方形纸片的长为
∴小丽不能裁出符合要求的纸片.
典例精析
∵ ,
∴正方形纸片的边长只有20cm,
1.估算13的算术平方根在( )
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
B
2.面积为19m2的正方形,它的边长介于( )
A.2m与3m之间 B.3m与4m之间
C.4m与5m之间 D.5m与6m之间
C
小试牛刀
1.估计的值在( )
A.1到2之间 B.2到3之间 C.3到4之间 D.4到5之间
2.已知:≈44.91,=14.0,则的值约为( )
A.32.41 B.1.40
C.3.241 D.4.491
C
D
课堂检测
4.若已知,,那么 .
3.若那么
.
11.18
0.3535
74500
课堂检测
1.比较大小:与0.5.
解:∵ 7>4,
∴
∴,
∴ 0.5 .
拓展训练
小数位数无限,且小数部分不循环的小数称为无限不循环小数.
算术平方根的规律
无限不循环小数
被开方数的小数点向右每移动2位,它的算术平方根的小数点就向右移动1位;
被开方数的小数点向左每移动2位,它的算术平方根的小数点就向左移动1位.
课堂小结
1.设n为正整数,且,则n的值为( )
A.5 B.6 C.7 D.8
D
2.若2<<3,则a的值可以是( )
A.﹣7 B. C. D.12
C
课后作业
3.设n为正整数,且n<
4.与最接近的整数是 ( )
A.7 B.8 C.9 D.10
C
C
课后作业
谢谢聆听
