17.1勾股定理 第1课时 课件(共18张PPT)
文档属性
| 名称 | 17.1勾股定理 第1课时 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 23:49:23 | ||
图片预览


文档简介
(共18张PPT)
第17.1 勾股定理
第1课时
人教版数学八年级下册
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
2.会用勾股定理进行简单的计算 .
情境引入
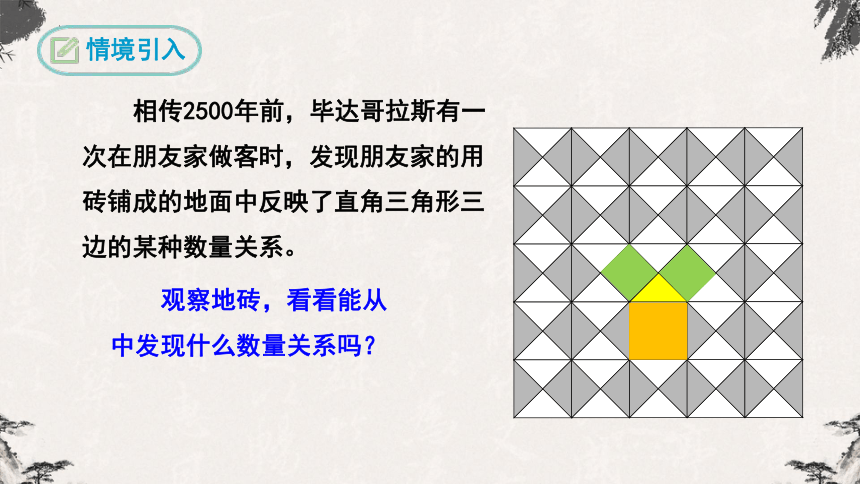
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
观察地砖,看看能从中发现什么数量关系吗?
互动新授
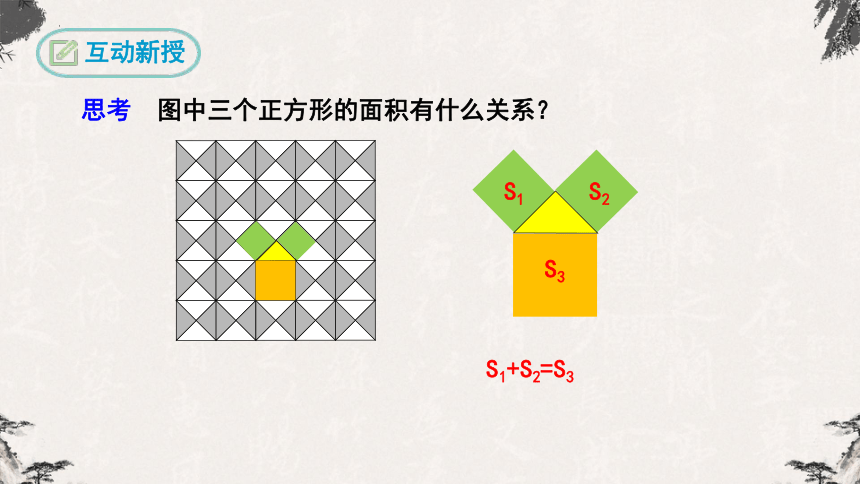
思考 图中三个正方形的面积有什么关系?
S1
S2
S3
S1+S2=S3
互动新授
S1
S2
S3
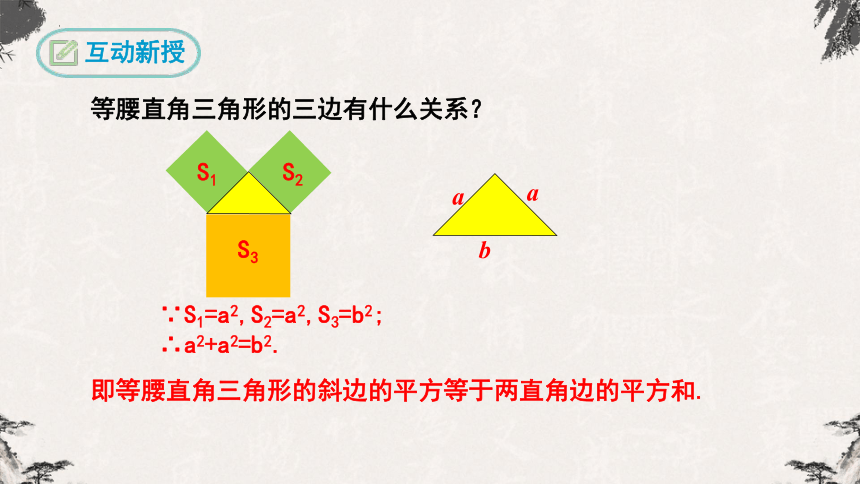
等腰直角三角形的三边有什么关系?
a
a
b
∵S1=a2,S2=a2,S3=b2;
∴a2+a2=b2.
即等腰直角三角形的斜边的平方等于两直角边的平方和.
互动新授
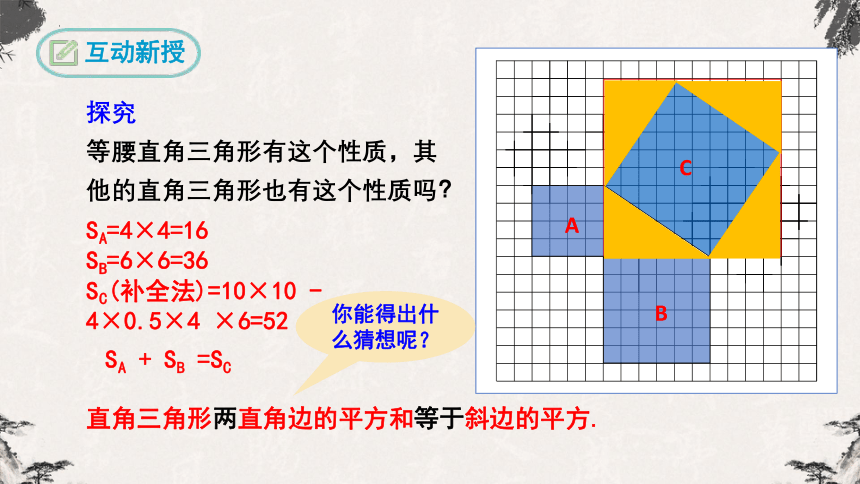
探究
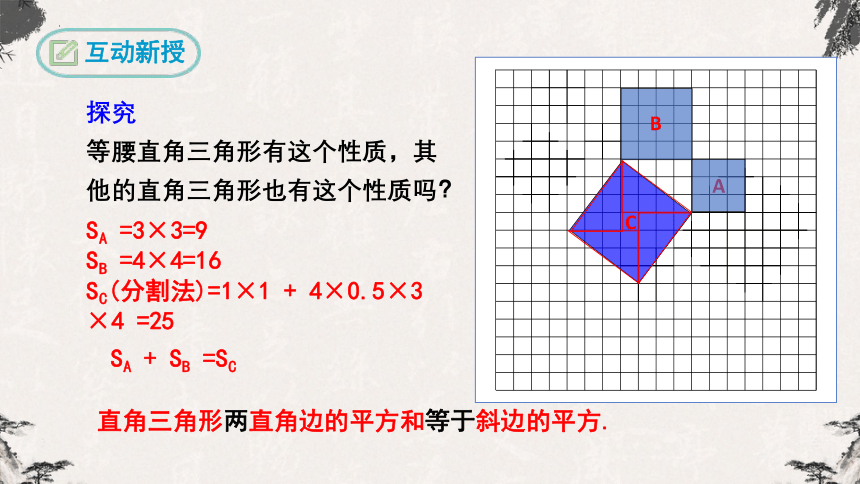
等腰直角三角形有这个性质,其他的直角三角形也有这个性质吗?
A
B
C
SA =3×3=9
SB =4×4=16
SC(分割法)=1×1 + 4×0.5×3 ×4 =25
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方.
互动新授
探究
等腰直角三角形有这个性质,其他的直角三角形也有这个性质吗?
A
B
C
SA=4×4=16
SB=6×6=36
SC(补全法)=10×10 - 4×0.5×4 ×6=52
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方.
你能得出什么猜想呢?
互动新授
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c .
那该如何推理证明呢?
证明命题1的方法有很多,下面介绍我国古人赵爽的证法.
互动新授
基本思路如下:
b
a
c
a+b
a
b
c
c
c
c
a
b
c
c
可以得到:a +b =c .
互动新授
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c .
上面我们证实了命题1的正确性.
命题1与直角三角形的边有关,我国把它称为勾股定理.
2.在R中,,如果,,那么的长是( )
A. B. C. D.或
C
1.在中,,,,则( )
A.4 B.3 C.2 D.1
A
小试牛刀
1.“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为,较短的直角边长为,若,大正方形的面积为,则小正方形的面积为__________.
5
课堂检测
2.以a,b,c为边的三角形是直角三角形的是( )
A.a=2,b=3,c=4 B.a=1,b= ,c=2
C.a=4,b=5,c=6 D.a=2,b=2,c=
B
课堂检测
3.如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
课堂检测
1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
拓展训练
勾股定理:
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意:
前提是在直角三角形中.
课堂小结
1.下列说法中,正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36cm
课后作业
谢谢聆听
第17.1 勾股定理
第1课时
人教版数学八年级下册
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理的一些文化历史背景,会用面积法来证明勾股定理,体会数形结合的思想.
2.会用勾股定理进行简单的计算 .
情境引入
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。
观察地砖,看看能从中发现什么数量关系吗?
互动新授
思考 图中三个正方形的面积有什么关系?
S1
S2
S3
S1+S2=S3
互动新授
S1
S2
S3
等腰直角三角形的三边有什么关系?
a
a
b
∵S1=a2,S2=a2,S3=b2;
∴a2+a2=b2.
即等腰直角三角形的斜边的平方等于两直角边的平方和.
互动新授
探究
等腰直角三角形有这个性质,其他的直角三角形也有这个性质吗?
A
B
C
SA =3×3=9
SB =4×4=16
SC(分割法)=1×1 + 4×0.5×3 ×4 =25
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方.
互动新授
探究
等腰直角三角形有这个性质,其他的直角三角形也有这个性质吗?
A
B
C
SA=4×4=16
SB=6×6=36
SC(补全法)=10×10 - 4×0.5×4 ×6=52
SA + SB =SC
直角三角形两直角边的平方和等于斜边的平方.
你能得出什么猜想呢?
互动新授
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c .
那该如何推理证明呢?
证明命题1的方法有很多,下面介绍我国古人赵爽的证法.
互动新授
基本思路如下:
b
a
c
a+b
a
b
c
c
c
c
a
b
c
c
可以得到:a +b =c .
互动新授
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a +b =c .
上面我们证实了命题1的正确性.
命题1与直角三角形的边有关,我国把它称为勾股定理.
2.在R中,,如果,,那么的长是( )
A. B. C. D.或
C
1.在中,,,,则( )
A.4 B.3 C.2 D.1
A
小试牛刀
1.“赵爽弦图”巧妙的利用面积关系证明了勾股定理,是我国古代数学的骄傲,如下图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长的直角边长为,较短的直角边长为,若,大正方形的面积为,则小正方形的面积为__________.
5
课堂检测
2.以a,b,c为边的三角形是直角三角形的是( )
A.a=2,b=3,c=4 B.a=1,b= ,c=2
C.a=4,b=5,c=6 D.a=2,b=2,c=
B
课堂检测
3.如图,在Rt△ABC中, ∠C=90°.
(1)若a=b=5,求c;
(2)若a=1,c=2,求b.
解:
(1)据勾股定理得
(2)据勾股定理得
C
A
B
课堂检测
1.在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图 ,
当BC为斜边时,如图 ,
4
3
A
C
B
4
3
C
A
B
拓展训练
勾股定理:
在Rt△ABC中, ∠C=90°,a,b为直角边,c为斜边,则有a2+b2=c2.
注意:
前提是在直角三角形中.
课堂小结
1.下列说法中,正确的是( )
A.已知a,b,c是三角形的三边,则a2+b2=c2
B.在直角三角形中两边和的平方等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以a2+b2=c2
D.在Rt△ABC中,∠B=90°,所以a2+b2=c2
C
2.图中阴影部分是一个正方形,则此正方形的面积为 .
8 cm
10 cm
36cm
课后作业
谢谢聆听
