17.1勾股定理 第2课时 课件(共19张PPT)
文档属性
| 名称 | 17.1勾股定理 第2课时 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-02 23:52:57 | ||
图片预览





文档简介
(共19张PPT)
第17.1 勾股定理
第2课时
人教版数学八年级下册
学习目标
1.能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长之间的联系,并进一步求出未知边的长度.
2.会运用勾股定理确定数轴上表示实数的点及解决网格问题.
3.会运用勾股定理解决简单的实际问题.
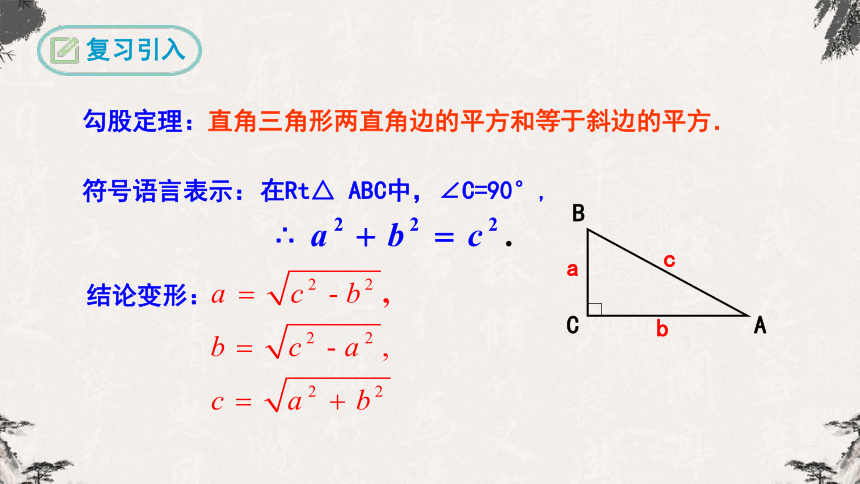
复习引入
直角三角形两直角边的平方和等于斜边的平方.
a
b
c
A
B
C
在Rt△ ABC中,∠C=90°,
∴
结论变形:
勾股定理:
符号语言表示:
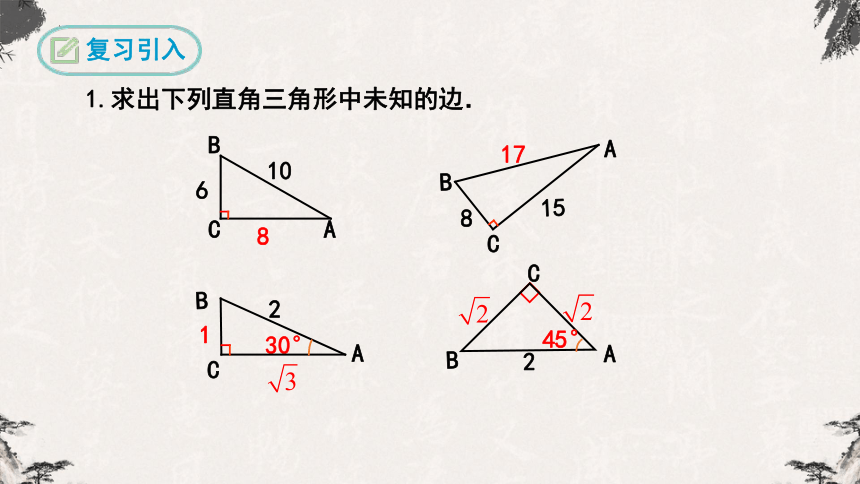
1.求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
A
C
B
A
C
B
8
17
1
复习引入
典例精析
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
分析:
1、由题干内容可知,门的高是2米,宽1米,木板 或
都不能通过,只能试试 能否通过.
2、门框对角线DB是斜着的最大长度,只要计算出 的长度,再与木板的 比较,只要_______,就知道能否通过.
横着
竖着
AC
宽
AC>2.2
斜着
典例精析
解:连接AC,
在Rt△ABD中,根据勾股定理,
得AC2=AB2+BC2=12+22=5.
AC= ≈2.24>2.2.
所以木板能从门框内通过.
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
典例精析
例2 如图,一架2.6m长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
分析:
1、梯子在下滑的过程中,_______不变,即________.
2、根据题干问题和图像,本题要求________,而______=______-______.
梯子的长
AB=CD
BD的长
BD
OD
OB
解:在Rt△AOB中,根据勾股定理,
得OB2=AB2-AO2=2.62-2.42=1,即OB=1
在Rt△COD中,根据勾股定理,
得OD2=CD2-CO2=CD2-(AO-AC)2
=2.62-1.92=3.15,即OD≈1.77
BD=OD-OB=1.77-1=0.77≠0.5
所以当梯子顶端A下滑0.5米时,梯子底端外移约0.77米
典例精析
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
互动新授
证明:在Rt△ABC 和Rt△A′B′C′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
互动新授
探究 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
互动新授
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
互动新授
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A.50米 B.120米
C.100米 D.130米
A
B
C
130
120
A
2.从电杆上离地面5m的C处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离是( )
A.24m B.12m
C. m D. cm
D
小试牛刀
1.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.8㎝,问吸管要做多长?
解:如图,杯内的吸管部分长为AC,
杯高AB=12cm,杯底直径BC=5cm;
Rt△ABC中,AB=12cm,BC=5cm;
由勾股定理得:
故吸管的长度最少要:13+4.8=17.8cm.
课堂检测
2.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
解:∵AC⊥BC,∴∠ACB=90°
根据勾股定理,得
∴BD=BC+CD=12+2=14(米)
答:发生火灾的住户窗口距离地面14米.
课堂检测
1.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
A
C
B
解:根据题意可以构建一直角三角形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
∴这棵树在折断之前的高度是10+6=16(米).
拓展训练
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
基本思路:
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
课堂小结
1.如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
课后作业
谢谢聆听
第17.1 勾股定理
第2课时
人教版数学八年级下册
学习目标
1.能从实际问题中抽象出直角三角形这一几何模型,利用勾股定理建立已知边与未知边长之间的联系,并进一步求出未知边的长度.
2.会运用勾股定理确定数轴上表示实数的点及解决网格问题.
3.会运用勾股定理解决简单的实际问题.
复习引入
直角三角形两直角边的平方和等于斜边的平方.
a
b
c
A
B
C
在Rt△ ABC中,∠C=90°,
∴
结论变形:
勾股定理:
符号语言表示:
1.求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
A
C
B
A
C
B
8
17
1
复习引入
典例精析
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
分析:
1、由题干内容可知,门的高是2米,宽1米,木板 或
都不能通过,只能试试 能否通过.
2、门框对角线DB是斜着的最大长度,只要计算出 的长度,再与木板的 比较,只要_______,就知道能否通过.
横着
竖着
AC
宽
AC>2.2
斜着
典例精析
解:连接AC,
在Rt△ABD中,根据勾股定理,
得AC2=AB2+BC2=12+22=5.
AC= ≈2.24>2.2.
所以木板能从门框内通过.
例1 一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
典例精析
例2 如图,一架2.6m长的梯子AB 斜靠在一竖直的墙AO上,这时AO 为2.4米.如果梯子的顶端A沿墙下滑0.5米,那么梯子底端B也外移0.5米吗?
分析:
1、梯子在下滑的过程中,_______不变,即________.
2、根据题干问题和图像,本题要求________,而______=______-______.
梯子的长
AB=CD
BD的长
BD
OD
OB
解:在Rt△AOB中,根据勾股定理,
得OB2=AB2-AO2=2.62-2.42=1,即OB=1
在Rt△COD中,根据勾股定理,
得OD2=CD2-CO2=CD2-(AO-AC)2
=2.62-1.92=3.15,即OD≈1.77
BD=OD-OB=1.77-1=0.77≠0.5
所以当梯子顶端A下滑0.5米时,梯子底端外移约0.77米
典例精析
思考 在八年级上册中,我们曾经通过画图得到结论:斜边和一条直角边分别相等的两个直角三角形全等.学习了勾股定理后,你能证明这一结论吗?
已知:如图,在Rt△ABC 和Rt△A′B′C′中,∠C=∠C′=90°,AB=A′B′,AC=A′C′.
求证:△ABC≌△A ′B ′C′ .
A
B
C
A
B
C′
′
′
互动新授
证明:在Rt△ABC 和Rt△A′B′C′中,
∠C=∠C′=90°,
根据勾股定理得
A
B
C
A
B
C′
′
′
互动新授
探究 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
互动新授
步骤:
1.在数轴上找到点A,使OA=3;
2.作直线l⊥OA,在l上取一点B,使AB=2;
3.以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点.
0
1
2
3
4
l
A
B
C
O
“数学海螺”
类似地,利用勾股定理可以作出长为 线段.
1
1
互动新授
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为 ( )
A.50米 B.120米
C.100米 D.130米
A
B
C
130
120
A
2.从电杆上离地面5m的C处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离是( )
A.24m B.12m
C. m D. cm
D
小试牛刀
1.一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.8㎝,问吸管要做多长?
解:如图,杯内的吸管部分长为AC,
杯高AB=12cm,杯底直径BC=5cm;
Rt△ABC中,AB=12cm,BC=5cm;
由勾股定理得:
故吸管的长度最少要:13+4.8=17.8cm.
课堂检测
2.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面2米,问:发生火灾的住户窗口距离地面多高?
解:∵AC⊥BC,∴∠ACB=90°
根据勾股定理,得
∴BD=BC+CD=12+2=14(米)
答:发生火灾的住户窗口距离地面14米.
课堂检测
1.在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
A
C
B
解:根据题意可以构建一直角三角形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
∴这棵树在折断之前的高度是10+6=16(米).
拓展训练
利用勾股定理解决实际问题的一般步骤:
(1)读懂题意,分析已知、未知间的关系;
(2)构造直角三角形;
(3)利用勾股定理等列方程;
(4)解决实际问题.
基本思路:
数学问题
直角三角形
勾股定理
实际问题
转化
构建
利用
决解
课堂小结
1.如图,有两棵树,一棵高8米,另一棵2米,两棵对相距8米.一只鸟从一棵树的树梢飞到另一棵的树梢,问小鸟至少飞行多少?
A
B
C
解:如图,过点A作AC⊥BC于点C.
由题意得AC=8米,BC=8-2=6(米),
答:小鸟至少飞行10米.
课后作业
谢谢聆听
