7.4 宇宙航行(共25张PPT)
文档属性
| 名称 | 7.4 宇宙航行(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-01-02 12:44:26 | ||
图片预览








文档简介
(共25张PPT)
7.4 宇宙航行
学习目标
1 宇宙速度
1.第一宇宙速度
(1)第一宇宙速度(环绕速度):
(2)第一宇宙速度的推导
方法一:地球对卫星的万有引力提供卫星做匀速圆周运动的向心力.G=m,v=当 h 增大时,v减小,所以在地球表面附近卫星的速度是它做圆周运动的最大速度. R >> h ,所以v==m/s=7.9km/s
方法二:在地面附近物体的重力近似等于地球对物体的万有引力,重力大小等于卫星做匀速圆周运动的向心力大小.
mg=m。R> > h ,所以=m/s=7.9km/s
v 1=7.9km/ s ,是人造地球卫星的最小发射速度,也是人造卫星绕地球做匀速圆周运动的最大速度.
思考:月球绕着地球转动要受到地球对它的吸引力,但是为什么月亮不会落到地面上来?
分析:由于月球在绕地球沿近似圆周的轨道运转,此时月球受到的地球对它的万有引力全部提供绕地球运转的向心力,即=m=m()2r,故月球不会落到地面上来.
1 宇宙速度
(3)注意事项
1)宇宙速度均指发射速度,卫星的环绕速度一定不大于其发射速度.
2)第一宇宙速度的其他三种叫法:最小发射速度、最大环绕速度、近地绕行速度.
3)不同天体有各自的第一宇宙速度.如果卫星的发射速度小于第一宇宙速度,卫星将落回天体表面.
4)地球的第一宇宙速度是卫星绕地球做速圆周运动的最大速度.若卫星的发射速度等于这个速度,卫星刚好能在地球表面附近做匀速圆周运动.
1 宇宙速度
2.第二宇宙速度
(1)第二宇宙速度:v2=11.2 km / s ,是使卫星挣脱地球引力束缚的最小发射速度.
(2)在地面附近发射飞行器,如果速度大于7.9 km / s ,而小于11.2 km / s ,它将沿椭圆轨道绕地球运行,地心就成为椭圆轨道的一个焦点.如果速度继续增大,达到或超过11.2 km / s 时(但需小于第三宇宙速度),它就会克服地球的引力,离开地球,成为绕太阳运动的一颗人造行星.
3.第三宇宙速度
第三宇宙速度:v3=16.7km/ s ,是使卫星挣脱太阳引力束缚而飞到太阳系外的最小发射速度.
第一、第二、第三宇宙速度的关系
1 宇宙速度
4.三种宇宙速度与运动情况的关系
(1)当 v < v 1时,被发射物体最终将落回地面;
(2)当v1≤v<2时,被发射物体将绕地球运动,成为地球卫星;
(3)当v2≤ v(4)当 v ≥ v3 时,被发射物体将挣脱太阳引力的束缚,飞出太阳系.
2 人造地球卫星
1.人造地球卫星的概念
环绕地球在空间轨道上运行的无人航天器.
2.人造地球卫星的特点
人造卫星绕地球运行时,地球对卫星的万有引力提供其做圆周运动的向心力.由G=m得v=,其中 M 为地球质量,为人造卫星的轨道半径.
3.人造地球卫星的轨道
所有卫星都在以地心为圆心的圆轨道或以地心为一个焦点的椭圆轨道上,人造地球卫星的轨道一般有三种,如图所示。
(1)赤道轨道:卫星轨道在赤道平面内,卫星始终处于赤道上方.
(2)极地轨道:卫星轨道平面与赤道平面垂直,卫星经过两极上空.
(3)其他轨道:卫星轨道和赤道平面成一定角度(不为90度).
2 人造地球卫星
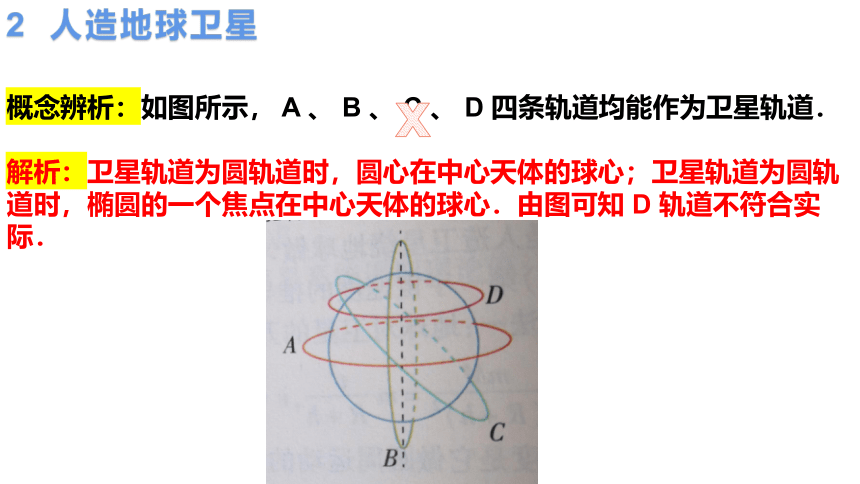
概念辨析:如图所示, A 、 B 、 C 、 D 四条轨道均能作为卫星轨道.
解析:卫星轨道为圆轨道时,圆心在中心天体的球心;卫星轨道为圆轨道时,椭圆的一个焦点在中心天体的球心.由图可知 D 轨道不符合实际.
x
2 人造地球卫星
现学现卖:如图所示为人造地球卫星的轨道示意图, LEO 是近地轨道,MEO是中轨道,GEO是地球同步轨道, GTO 是地球同步转移轨道,已知地球的半径 R =6400km,该图中ME0轨道上卫星的周期约为 (图中数据为卫星近地点、远地点离地面的高度)
A .3 h B .8 h C .15 h D .20h
A
3 人造地球卫星的运行规律
(1)将各种卫星绕地球的运动都近似看成速圆周运动,轨道半径r= R + h ,R 为地球半径, h 为卫星距地面的高度,卫星环绕线速度、角速度、周期、向心加速度与轨道半径的关系如下
(1)由G=m得v=, h 越大,轨道半径越大,线速度越小.
(2)由G=mω2(R+h)得,ω=,h 越大,轨道半径越大,角速
(3)由G=m 得T=, h 越大,轨道半径越大,周期越大。
(4)由 G=ma得a=, h 越大,轨道半径越大,向心加速度越小
3 人造地球卫星的运行规律
(2)结论:
卫星绕地球运行的线速度、角速度、周期及向心加速度与卫星质量无关.离地面越高(轨道半径越大)的卫星,向心加速度越小,运行速度(线速度、角速度)越小,周期越大,从地面发射时需要的初速度越大.
思考:既然卫星离地面越远,速率越小,为什么发射高空卫星反而不易?
发射人造地球卫星时,地球的引力为阻力,卫星上升得越高,需要克服地球引力做功越多.因而离地面越远,发射卫星所需的能量就越多。
3 人造地球卫星的运行规律
3 四个重要结论
设质量为m的天体绕另一质量为 M 的中心天体做半径为r的匀速圆周运动,则有如表所示的结论
3 人造地球卫星的运行规律
运动常量 基本公式F万=Fn 近地绕行(r=R,mg=G=Fn) 远地绕行
(r>R,F万=G=Fn)
v G=m v== v=
ω G=mω2r ω== ω=
T G=m T==2π T=
an G=man an==g an=
由以上表格可知,r越大, T 越大,v、 ω 、an越小。
由此可以看出环绕天体绕中心天体做匀速圆周运动的线速度、角速度、周期及向心加速度等均与环绕天体的质量无关,只与中心天体的质量 M 和轨道半径 r 有关
4 近地卫星与地球同步卫星
1.近地卫星
近地卫星的轨道半径r可以近似地认为等于地球半径 R ,其线速度大小为v1=7.9 km / s ;由v=可得其周期T≈84min
由之前讨论可知,7.9 km / s 和84 min 分别是绕地球做匀速圆周运动的人造卫星的最大线速度和最小周期
结论:在所有人造地球卫星中,近地卫星的线速度、角速度、向心加速度最大,周期最小.
4 近地卫星与地球同步卫星
2.地球同步卫星
(1)"同步"的含义就是和地球保持相对静止,所以其周期等于地球自转周期.
(2)特点
①定周期:所有同步卫星周期 T ≈24h.
②定点:相对地面静止且在赤道上的某点的正上方。
③定轨道:同步卫星轨道必须在地球赤道的正上方,运转方向必须跟地球自转方向一致,即由西向东
④定高度:由G=m=m(R+h)可得,同步卫星离地面高度h=-R≈3.58x107m≈6R
4 近地卫星与地球同步卫星
2.地球同步卫星
(2)特点
⑤定速度:由于同步卫星高度确定,则其轨道半径确定,因此线速度、角速度小均不变,
⑥定加速度:由于同步卫星高度确定,则其轨道半径确定,因此向心加速度大也不变
注意
如果仅与地球自转周期相同而不定点于赤道上空,该卫星就不能与地球保持相对静止.
4 近地卫星与地球同步卫星
现学现卖:关于地球同步卫星,下列说法正确的是
A .它处于平衡状态且具有一定的高度
B .它的向心加速度等于9.8 m /s2
C .它的周期是24h,且轨道平面与赤道平面重合
D .它绕行的速度大于7.9 km / s
C
课后练习
课后练习
BC
课后练习
课后练习
AB
课后练习
A
课后练习
BD
课后练习
A
谢谢
7.4 宇宙航行
学习目标
1 宇宙速度
1.第一宇宙速度
(1)第一宇宙速度(环绕速度):
(2)第一宇宙速度的推导
方法一:地球对卫星的万有引力提供卫星做匀速圆周运动的向心力.G=m,v=当 h 增大时,v减小,所以在地球表面附近卫星的速度是它做圆周运动的最大速度. R >> h ,所以v==m/s=7.9km/s
方法二:在地面附近物体的重力近似等于地球对物体的万有引力,重力大小等于卫星做匀速圆周运动的向心力大小.
mg=m。R> > h ,所以=m/s=7.9km/s
v 1=7.9km/ s ,是人造地球卫星的最小发射速度,也是人造卫星绕地球做匀速圆周运动的最大速度.
思考:月球绕着地球转动要受到地球对它的吸引力,但是为什么月亮不会落到地面上来?
分析:由于月球在绕地球沿近似圆周的轨道运转,此时月球受到的地球对它的万有引力全部提供绕地球运转的向心力,即=m=m()2r,故月球不会落到地面上来.
1 宇宙速度
(3)注意事项
1)宇宙速度均指发射速度,卫星的环绕速度一定不大于其发射速度.
2)第一宇宙速度的其他三种叫法:最小发射速度、最大环绕速度、近地绕行速度.
3)不同天体有各自的第一宇宙速度.如果卫星的发射速度小于第一宇宙速度,卫星将落回天体表面.
4)地球的第一宇宙速度是卫星绕地球做速圆周运动的最大速度.若卫星的发射速度等于这个速度,卫星刚好能在地球表面附近做匀速圆周运动.
1 宇宙速度
2.第二宇宙速度
(1)第二宇宙速度:v2=11.2 km / s ,是使卫星挣脱地球引力束缚的最小发射速度.
(2)在地面附近发射飞行器,如果速度大于7.9 km / s ,而小于11.2 km / s ,它将沿椭圆轨道绕地球运行,地心就成为椭圆轨道的一个焦点.如果速度继续增大,达到或超过11.2 km / s 时(但需小于第三宇宙速度),它就会克服地球的引力,离开地球,成为绕太阳运动的一颗人造行星.
3.第三宇宙速度
第三宇宙速度:v3=16.7km/ s ,是使卫星挣脱太阳引力束缚而飞到太阳系外的最小发射速度.
第一、第二、第三宇宙速度的关系
1 宇宙速度
4.三种宇宙速度与运动情况的关系
(1)当 v < v 1时,被发射物体最终将落回地面;
(2)当v1≤v<2时,被发射物体将绕地球运动,成为地球卫星;
(3)当v2≤ v
2 人造地球卫星
1.人造地球卫星的概念
环绕地球在空间轨道上运行的无人航天器.
2.人造地球卫星的特点
人造卫星绕地球运行时,地球对卫星的万有引力提供其做圆周运动的向心力.由G=m得v=,其中 M 为地球质量,为人造卫星的轨道半径.
3.人造地球卫星的轨道
所有卫星都在以地心为圆心的圆轨道或以地心为一个焦点的椭圆轨道上,人造地球卫星的轨道一般有三种,如图所示。
(1)赤道轨道:卫星轨道在赤道平面内,卫星始终处于赤道上方.
(2)极地轨道:卫星轨道平面与赤道平面垂直,卫星经过两极上空.
(3)其他轨道:卫星轨道和赤道平面成一定角度(不为90度).
2 人造地球卫星
概念辨析:如图所示, A 、 B 、 C 、 D 四条轨道均能作为卫星轨道.
解析:卫星轨道为圆轨道时,圆心在中心天体的球心;卫星轨道为圆轨道时,椭圆的一个焦点在中心天体的球心.由图可知 D 轨道不符合实际.
x
2 人造地球卫星
现学现卖:如图所示为人造地球卫星的轨道示意图, LEO 是近地轨道,MEO是中轨道,GEO是地球同步轨道, GTO 是地球同步转移轨道,已知地球的半径 R =6400km,该图中ME0轨道上卫星的周期约为 (图中数据为卫星近地点、远地点离地面的高度)
A .3 h B .8 h C .15 h D .20h
A
3 人造地球卫星的运行规律
(1)将各种卫星绕地球的运动都近似看成速圆周运动,轨道半径r= R + h ,R 为地球半径, h 为卫星距地面的高度,卫星环绕线速度、角速度、周期、向心加速度与轨道半径的关系如下
(1)由G=m得v=, h 越大,轨道半径越大,线速度越小.
(2)由G=mω2(R+h)得,ω=,h 越大,轨道半径越大,角速
(3)由G=m 得T=, h 越大,轨道半径越大,周期越大。
(4)由 G=ma得a=, h 越大,轨道半径越大,向心加速度越小
3 人造地球卫星的运行规律
(2)结论:
卫星绕地球运行的线速度、角速度、周期及向心加速度与卫星质量无关.离地面越高(轨道半径越大)的卫星,向心加速度越小,运行速度(线速度、角速度)越小,周期越大,从地面发射时需要的初速度越大.
思考:既然卫星离地面越远,速率越小,为什么发射高空卫星反而不易?
发射人造地球卫星时,地球的引力为阻力,卫星上升得越高,需要克服地球引力做功越多.因而离地面越远,发射卫星所需的能量就越多。
3 人造地球卫星的运行规律
3 四个重要结论
设质量为m的天体绕另一质量为 M 的中心天体做半径为r的匀速圆周运动,则有如表所示的结论
3 人造地球卫星的运行规律
运动常量 基本公式F万=Fn 近地绕行(r=R,mg=G=Fn) 远地绕行
(r>R,F万=G=Fn)
v G=m v== v=
ω G=mω2r ω== ω=
T G=m T==2π T=
an G=man an==g an=
由以上表格可知,r越大, T 越大,v、 ω 、an越小。
由此可以看出环绕天体绕中心天体做匀速圆周运动的线速度、角速度、周期及向心加速度等均与环绕天体的质量无关,只与中心天体的质量 M 和轨道半径 r 有关
4 近地卫星与地球同步卫星
1.近地卫星
近地卫星的轨道半径r可以近似地认为等于地球半径 R ,其线速度大小为v1=7.9 km / s ;由v=可得其周期T≈84min
由之前讨论可知,7.9 km / s 和84 min 分别是绕地球做匀速圆周运动的人造卫星的最大线速度和最小周期
结论:在所有人造地球卫星中,近地卫星的线速度、角速度、向心加速度最大,周期最小.
4 近地卫星与地球同步卫星
2.地球同步卫星
(1)"同步"的含义就是和地球保持相对静止,所以其周期等于地球自转周期.
(2)特点
①定周期:所有同步卫星周期 T ≈24h.
②定点:相对地面静止且在赤道上的某点的正上方。
③定轨道:同步卫星轨道必须在地球赤道的正上方,运转方向必须跟地球自转方向一致,即由西向东
④定高度:由G=m=m(R+h)可得,同步卫星离地面高度h=-R≈3.58x107m≈6R
4 近地卫星与地球同步卫星
2.地球同步卫星
(2)特点
⑤定速度:由于同步卫星高度确定,则其轨道半径确定,因此线速度、角速度小均不变,
⑥定加速度:由于同步卫星高度确定,则其轨道半径确定,因此向心加速度大也不变
注意
如果仅与地球自转周期相同而不定点于赤道上空,该卫星就不能与地球保持相对静止.
4 近地卫星与地球同步卫星
现学现卖:关于地球同步卫星,下列说法正确的是
A .它处于平衡状态且具有一定的高度
B .它的向心加速度等于9.8 m /s2
C .它的周期是24h,且轨道平面与赤道平面重合
D .它绕行的速度大于7.9 km / s
C
课后练习
课后练习
BC
课后练习
课后练习
AB
课后练习
A
课后练习
BD
课后练习
A
谢谢
