2022-2023学年山东省青岛市城阳区七年级(上)期末数学试卷(pdf、含解析)
文档属性
| 名称 | 2022-2023学年山东省青岛市城阳区七年级(上)期末数学试卷(pdf、含解析) | 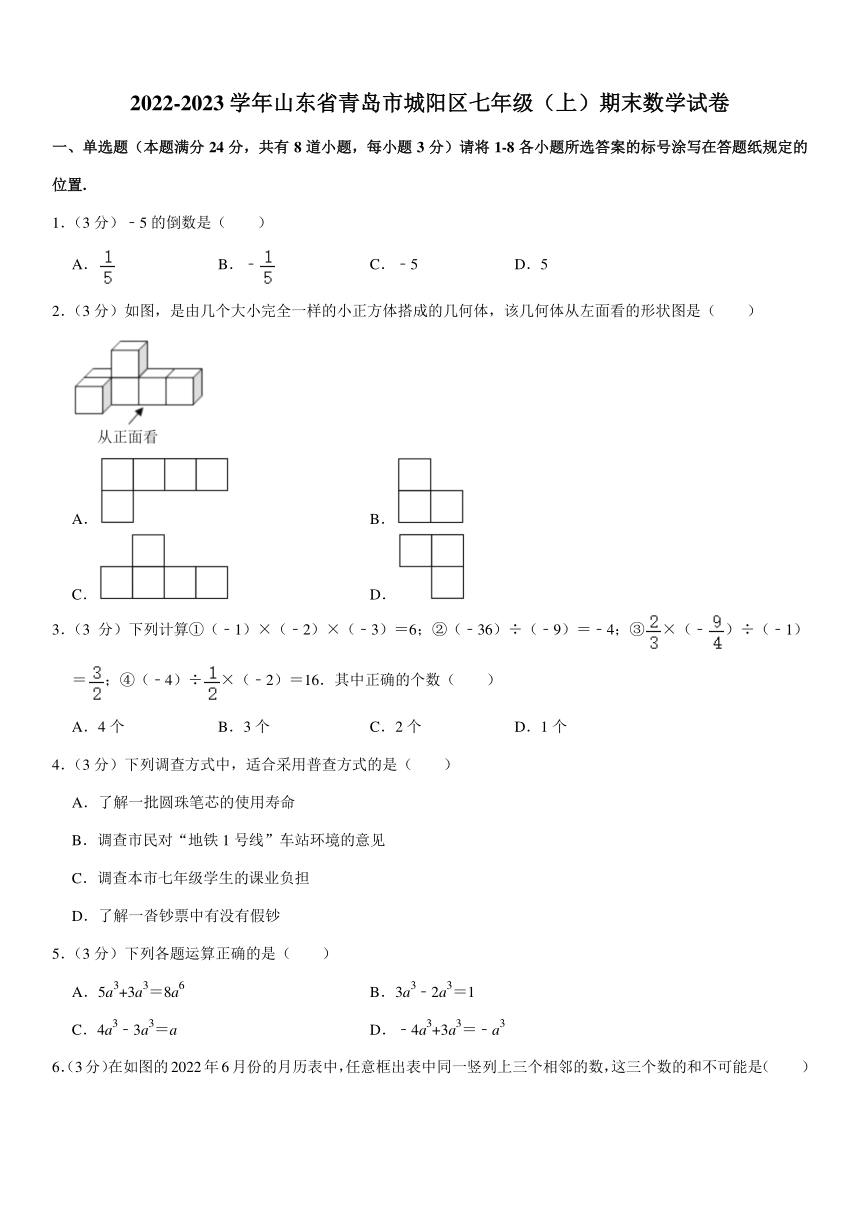 | |
| 格式 | zip | ||
| 文件大小 | 553.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-03 10:17:37 | ||
图片预览




文档简介
2022-2023 学年山东省青岛市城阳区七年级(上)期末数学试卷
一、单选题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 1-8 各小题所选答案的标号涂写在答题纸规定的
位置.
1.(3 分)﹣5 的倒数是( )
A. B.﹣ C.﹣5 D.5
2.(3 分)如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
3.(3 分)下列计算①(﹣1)×(﹣2)×(﹣3)=6;②(﹣36)÷(﹣9)=﹣4;③ ×(﹣ )÷(﹣1)
= ;④(﹣4)÷ ×(﹣2)=16.其中正确的个数( )
A.4 个 B.3 个 C.2 个 D.1 个
4.(3 分)下列调查方式中,适合采用普查方式的是( )
A.了解一批圆珠笔芯的使用寿命
B.调查市民对“地铁 1 号线”车站环境的意见
C.调查本市七年级学生的课业负担
D.了解一沓钞票中有没有假钞
5.(3 分)下列各题运算正确的是( )
3 3 6 3 3
A.5a +3a =8a B.3a ﹣2a =1
3 3 3 3 3
C.4a ﹣3a =a D.﹣4a +3a =﹣a
6.(3分)在如图的 2022年 6月份的月历表中,任意框出表中同一竖列上三个相邻的数,这三个数的和不可能是( )
A.27 B.51 C.75 D.69
7.(3 分)有理数 a、b、c 在数轴上的对应点如图所示,化简代数式:|a﹣b|+|a+b|﹣3|c﹣a|=( )
A.﹣3c B.a﹣3c C.﹣2a﹣2b﹣3c D.﹣4a+3c
8.(3 分)为使全国人民都过上幸福的小康生活,近年来各地扶贫办致力于帮扶当地区特色产品走进市民的菜篮子,
助力更多优质农产品走出地区、走向全国.已知有一扶贫农产品去年和今年两年的销售总额为 180 万元,其中该
扶贫农产品去年的价格为 15 元/千克,今年的价格为 12 元/千克,今年的销售产量比去年增长了 25%.今年该扶
贫农产品销售( )千克.
A.60000 B.75000 C.6000 D.7500
二、填空题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 9-16 各小题的答案填写在答题纸规定的位置.
9.(3 分) 的系数是 .
10.(3 分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地
位,其星载原子钟的精度,已经提升到了每 3000000 年误差 1 秒.数 3000000 用科学记数法表示为 .
a+2 2 5 b b
11.(3 分)如果单项式 x y 与 2x y 是同类项,那么 a = .
3 2 3
12.(3 分)化简:(6a ﹣a ﹣4a﹣3)﹣(3a ﹣2a+1)= .
13.(3 分)如图,∠AOB 是直角,∠BOC=36°,OD 平分∠AOC,则∠BOD= °.
14.(3 分)一个两位数,十位数字是个位数字的 3 倍,将两个数字对调后得到的新两位数比原来的两位数小 36,
原来两位数是 .
15.(3 分)将一个底面直径是 10 厘米、高为 60 厘米的圆柱锻压成底面直径为 30 厘米的圆柱,则锻压后圆柱的高
为 厘米.
16.(3 分)卡塔尔世界杯吸引了很多球迷的观看.某观看大厅观众区分为三部分,中间部分为固定座位数,每排
13 座,两边成扇形,第一排两边都为 5 座,第二排两边都为 7 座,第三排两边都为 9 座,往后按照此规律依次
类推 若此演出大厅共有 15 排座位,则能同时容纳 人观看.
三、作图题(本题满分 4 分)尺规作图,不写作法,保留作图痕迹.
17.(4 分)已知:线段 a、b,求作:线段 AB,使 AB=3b﹣a.
四、解答题(本题共有 8 道小题,满分 68 分)
18.(12 分)计算与化简求值
(1) ;
3 2
(2) ﹣[(﹣3 )﹣4 ];
3 2 3 2
(3)先化简再求值:﹣ (3x +6x +18)+ (x ﹣4x +4),其中 x=﹣ .
19.(8 分)解方程
(1) x=﹣1;
(2) =3(x﹣4).
20.(6 分)已知:线段 AB=20cm,点 C、D 为线段 AB 上两点,且 BC= AB,AD= AB,点 M 和点 N 分别是
线段 AC 和 BD 的中点.求:线段 MN 的长.
21.(6 分)已知:∠COD 在∠AOB 的内部,且∠AOB=160°,∠COD= ∠AOB,射线 OE 平分∠AOD,∠COE
=18°.
求:(1)∠AOD 的度数;
(2)∠BOC 的度数.
22.(8 分)我区某学校组织开展了疫情防控知识的培训.为了解学生们对疫情防控知识的学习情况,学校准备采用
以下调查方式中的一种进行调查:
①从七年级一班随机选取 20 名学生作为调查对象进行调查;
②从八年级中随机选取 300 名学生作为调查对象进行调查;
③从全校学生学籍档案中随机抽取 300 名学生作为调查对象进行调查.
按照一种比较合理的调查方式所得到的数据后,学校按成绩分成五个等级,并绘制了如下不完整的统计图
等级 成绩
A 50≤x<
60
B 60≤x<
70
C 70≤x<
80
D 80≤x<
90
E 90≤x≤
100
(1)在上述调查方式中,你认为比较合理的一个是 (填序号);
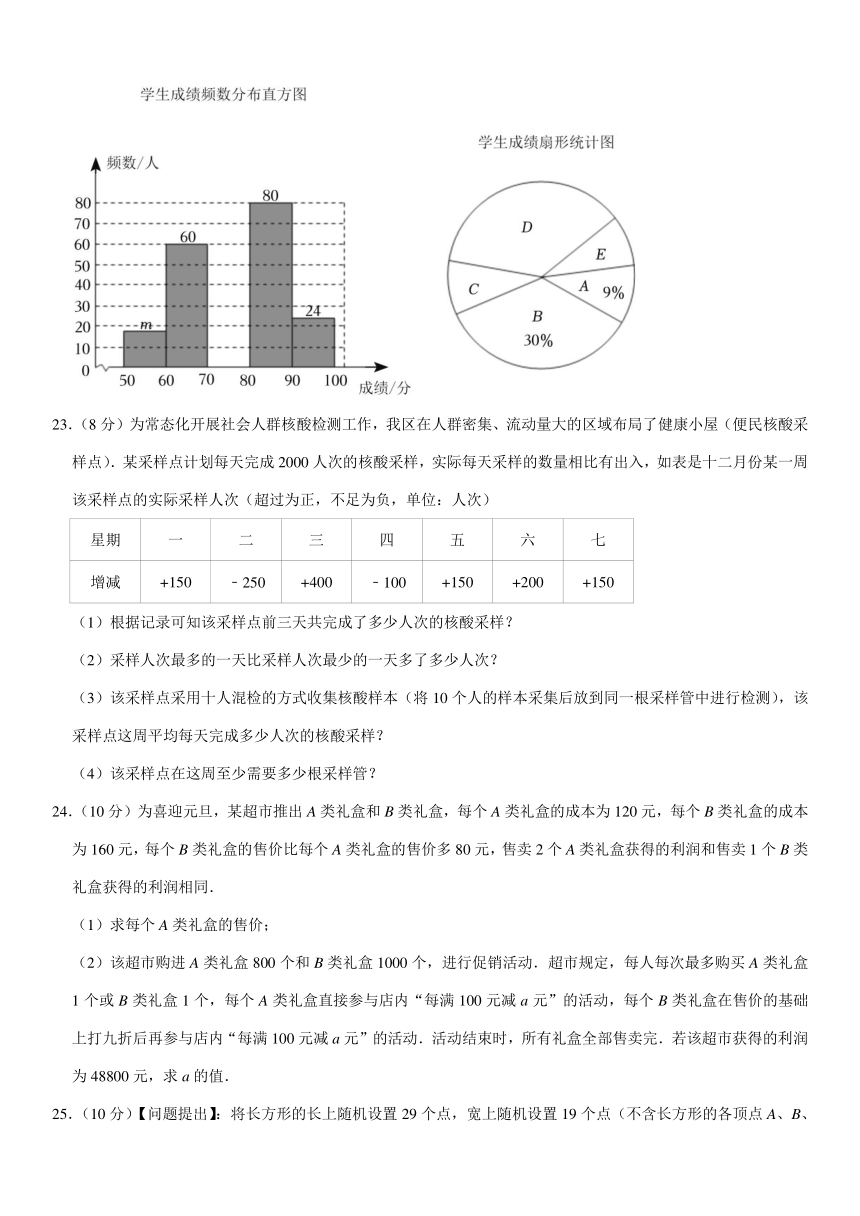
(2)在学生成绩频数分布直方图中 m 的值为 人;
(3)在学生成绩扇形统计图中,D 项所在的圆心角的度数为 °;
(4)若成绩在 80 分及以上为优秀,全校共有 1800 名学生,估计成绩优秀的学生有多少人?
23.(8 分)为常态化开展社会人群核酸检测工作,我区在人群密集、流动量大的区域布局了健康小屋(便民核酸采
样点).某采样点计划每天完成 2000 人次的核酸采样,实际每天采样的数量相比有出入,如表是十二月份某一周
该采样点的实际采样人次(超过为正,不足为负,单位:人次)
星期 一 二 三 四 五 六 七
增减 +150 ﹣250 +400 ﹣100 +150 +200 +150
(1)根据记录可知该采样点前三天共完成了多少人次的核酸采样?
(2)采样人次最多的一天比采样人次最少的一天多了多少人次?
(3)该采样点采用十人混检的方式收集核酸样本(将 10 个人的样本采集后放到同一根采样管中进行检测),该
采样点这周平均每天完成多少人次的核酸采样?
(4)该采样点在这周至少需要多少根采样管?
24.(10 分)为喜迎元旦,某超市推出 A 类礼盒和 B 类礼盒,每个 A 类礼盒的成本为 120 元,每个 B 类礼盒的成本
为 160 元,每个 B 类礼盒的售价比每个 A 类礼盒的售价多 80 元,售卖 2 个 A 类礼盒获得的利润和售卖 1 个 B 类
礼盒获得的利润相同.
(1)求每个 A 类礼盒的售价;
(2)该超市购进 A 类礼盒 800 个和 B 类礼盒 1000 个,进行促销活动.超市规定,每人每次最多购买 A 类礼盒
1 个或 B 类礼盒 1 个,每个 A 类礼盒直接参与店内“每满 100 元减 a 元”的活动,每个 B 类礼盒在售价的基础
上打九折后再参与店内“每满 100 元减 a 元”的活动.活动结束时,所有礼盒全部售卖完.若该超市获得的利润
为 48800 元,求 a 的值.
25.(10 分)【问题提出】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、
C、D,且相对的边点的位置相同),如图连接各边对应的点,则图中一共有多少个长方形(包括正方形)?
【问题探究】:为解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:
(1)探究一:将一条线段上随机设置 n 个点,图中一共可以形成多少条线段?
如图 1,当 n=0 时,图中线段有:线段 AB,共 1 条线段;
如图 2,当 n=1 时,以 A 为端点的线段有:线段 AC 和线段 AB,共 2 条线段;以 C 为端点的有:线段 CB,共
1 条线段,故图中共有 2+1=3 条线段;
如图 3,当 n=2 时,以 A 为端点的线段有:线段 AC,线段 AD 和线段 AB,共 3 条线段;以 C 为端点的有:线
段 CD 和线段 CB,共 2 条线段;以 D 为端点的有:线段 DB,共 1 条线段,故图中共有 3+2+1=6 条线段;
小结:当随机设置了 n 个点后,一共可以形成 条线段.(用含 n 的代数式表示)
(2)探究二:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,则一共有多少个长方形(包括正方形)?
首先我们先探究宽上不设置点的情况.
如图 4﹣1,当 m=0,n=0 时,图中一共有 1 个长方形.
如图 4﹣2,当 m=1,n=0 时,图中一共有 3 个长方形.
如图 4﹣3,当 m=2,n=0 时,图中一共有 6 个长方形.
小结:当长方形的长上随机设置 m 个点,宽上不设置点,一共有 个长方形.(用含 m 的代数式表示)
同理,当长方形的长上不设置点,宽上随机设置 n 个点,一共有 个长方形.(用含 n 的代数式表示)
如图 5﹣1,当 m=1,n=1 时,长上共形成 3 条线段,宽上共形成 3 条线段,图中一共有 9 个长方形(包括正方
形).
如图 5﹣2,当 m=1,n=2 时,长上共形成 3 条线段,宽上共形成 6 条线段,图中一共有 18 个长方形(包括正
方形).
如图 5﹣3,当 m=2,n=1 时,长上共形成 6 条线段,宽上共形成 3 条线段,图中一共有 18 个长方形(包括正
方形).
如图 5﹣4,当 m=2,n=2 时,长上共形成 6 条线段,宽上共形成 6 条线段,图中一共有 36 个长方形(包括正
方形).
小结:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,连接各边对应的点,则图中一共有 个
长方形(包括正方形).(用含 m、n 的代数式表示)
【问题解决】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、C、D,
且相对的边点的位置相同),如图连接各边对应的点,则图中一共有 个长方形(包括正方形).(直接写
出最后计算结果)
2022-2023 学年山东省青岛市城阳区七年级(上)期末数学试卷
参考答案与试题解析
一、单选题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 1-8 各小题所选答案的标号涂写在答题纸规定的
位置.
1.【解答】解:∵(﹣5)×(﹣ )=1,
∴﹣5 的倒数是﹣ .
故选:B.
2.【解答】解:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:B.
3.【解答】解:①(﹣1)×(﹣2)×(﹣3)=﹣6,故原题计算错误;
②(﹣36)÷(﹣9)=4,故原题计算错误;
③ ×(﹣ )÷(﹣1)= ,故原题计算正确;
④(﹣4)÷ ×(﹣2)=16,故原题计算正确,
正确的计算有 2 个,
故选:C.
4.【解答】解:A、了解一批圆珠笔芯的使用寿命,适合采用抽样调查方式,不符合题意;
B、调查市民对“地铁 1 号线”车站环境的意见,适合采用抽样调查方式,不符合题意;
C、调查本市七年级学生的课业负担,适合采用抽样调查方式,不符合题意;
D、了解一沓钞票中有没有假钞,适合采用普查方式,符合题意;
故选:D.
3 3 3
5.【解答】解:A、5a +3a =8a ,原计算错误,故此选项不符合题意;
3 3 3
B、3a ﹣2a =2a ,原计算错误,故此选项不符合题意;
3 3 3
C、4a ﹣3a =a ,原计算错误,故此选项不符合题意;
3 3 3
D、﹣4a +3a =﹣a ,原计算正确,故此选项符合题意.
故选:D.
6.【解答】解:设框出的最小数是 x,则另外两个数是 x+7,x+14,
这三个数的和是 x+x+7+x+14=3x+21,
若 3x+21=27,则 x=2,框出的三个数是 2,9,16,故 A 不符合题意;
若 3x+21=51,则 x=10,框出的三个数是 10,17,24,故 B 不符合题意;
若 3x+21=75,则 x=18,框出的三个数是 18,25,32,
从图可知不能框出 18,25,32,故 C 符合题意;
若 3x+21=69,则 x=16,框出的三个数是 16,23,30,故 D 不符合题意;
故选:C.
7.【解答】解:根据数轴上点的位置得:a<b<0<c,
∴a﹣b<0,a+b<0,c﹣a>0,
则原式=b﹣a﹣a﹣b﹣3c+3a=a﹣3c,
故选:B.
8.【解答】解:设去年该扶贫农产品销售 x 千克,则今年该扶贫农产品销售(1+25%)x 千克,
根据题意得:15x+12×(1+25%)x=1800000,
解得 x=60000,
∴(1+25%)x=75000,
∴今年该扶贫农产品销售 75000 千克,
故选:B.
二、填空题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 9-16 各小题的答案填写在答题纸规定的位置.
9.【解答】解: 的系数是﹣ .
故答案为:﹣ .
6
10.【解答】解:数 3000000 用科学记数法表示为 3×10 ,
6
故答案为:3×10 .
a+2 2 5 b
11.【解答】解:∵单项式 x y 与 2x y 是同类项,
∴a+2=5,b=2,
∴a=3,
b 2
∴a =3 =9.
故答案为:9.
3 2 3
12.【解答】解:(6a ﹣a ﹣4a﹣3)﹣(3a ﹣2a+1)
3 2 3
=6a ﹣a ﹣4a﹣3﹣3a +2a﹣1
3 2
=3a ﹣a ﹣2a﹣4,
3 2
故答案为:3a ﹣a ﹣2a﹣4.
13.【解答】解:∵∠AOB 是直角,∠BOC=36°,
∴∠AOC=90°+36°=126°,
∵OD 平分∠AOC,
∴∠COD= ∠AOC=63°,
∴∠BOD=∠COD﹣∠BOC=63°﹣36°=27°,
故答案为:27.
14.【解答】解:设原来两位数的个位数字是 x,则它的十位数字是 3x,
根据题意得 10×3x+x﹣(10x+3x)=36,
解得 x=2,
所以 3x=6,
所以原来的两位是 62,
故答案为:62.
15.【解答】解:设锻压后圆柱的高为 x 厘米,由题意得:
2 2
π( ) x=π( ) ×60,
解得:x= .
答:锻压后圆柱的高为 厘米.
故答案为: .
16.【解答】解:根据题意有,
5+(15﹣1)×2=5+28=33
两边部分的座位数为:2×(5+7+9+...+33)=2× =570(座),
中间部分的座位数为:13×15=195(座),
195+570=765(座),
∴能同时容纳 765 人观看.
故答案为:765
三、作图题(本题满分 4 分)尺规作图,不写作法,保留作图痕迹.
17.【解答】解:如图:
AB 即为所求.
四、解答题(本题共有 8 道小题,满分 68 分)
18.【解答】解:(1)原式=﹣8×(﹣2+ ﹣ )
=﹣2×(﹣8)+ ×(﹣8)﹣ ×(﹣8)
=16﹣4+1
=12+1
=13.
(2)原式=5÷(﹣ )﹣(﹣27﹣16)
=﹣60﹣(﹣43)
=﹣60+43
=﹣17.
3 2 3 2
(3)原式=﹣ x ﹣x ﹣3+ x ﹣2x +2
2
=﹣3x ﹣1,
当 x=﹣ 时,
原式=﹣3× ﹣1
=﹣ ﹣1
= .
19.【解答】解:(1)去分母得:4(x﹣5)﹣3x=﹣12,
去括号得:4x﹣20﹣3x=﹣12,
解得:x=8;
(2)去括号得:x﹣2x﹣1=3x﹣12,
移项得:x﹣2x﹣3x=﹣12+1,
合并得:﹣4x=﹣11,
解得:x= .
20.【解答】解:∵AB=20cm,BC= AB,AD= AB,
∴BC=4cm,AD=5cm,
∴AC=AB﹣BC=16cm,BD=AB﹣AD=15cm,
∵M、N 分别是线段 AC、BD 的中点,
∴AM=CM= AC=8cm,BN=DN= BD= cm,
∴MN=AB﹣AM﹣BN=20cm﹣8cm﹣ cm= cm.
21.【解答】解:(1)∵∠AOB=160°,∠COE=18°,
∴∠COD= ∠AOB ×160°=40°,
∴∠EOD=∠EOC+∠COD=18°+40°=58°,
∵射线 OE 平分∠AOD,
∴∠AOE=∠EOD= ∠AOD,
∴∠AOD=2∠EOD=2×58°=116°;
∴∠AOD 的度数为 116°;
(2)由(1)得∠AOE=∠EOD=58°,
∵∠COE=18°,∠AOB=160°,
∴∠AOC=∠AOE+∠COE=58°+18°=76°,
∴∠BOC=∠AOB﹣∠AOC=160°﹣76°=84°.
∴∠BOC 的度数为 84°.
22.【解答】解:(1)由题意可得,从全校学生学籍档案中随机抽取 300 名学生作为调查对象进行调查,比较合理,
故答案为:③;
(2)60÷30%=200(人),
m=200×9%=18,
故答案为:18;
(3)360°× =144°,
故答案为:144;
(4)1800× =936(人),
答:估计成绩优秀的学生有 936 人.
23.【解答】解:(1)[+100+(﹣250)+(+400)]+2000×3
=250+6000
=6250(人次),
答:该采样点前三天共完成了 6250 人次的核酸采样;
(2)+400﹣(﹣250)=400+250=650(人次),
答:采样人次最多的一天比采样人次最少的一天多了 650 人次;
(3)(100﹣250+400﹣250﹣100+350+150)+2000×7
=500+14000
=14500(人次),
答:该采样点这周平均每天完成 14500 人次的核酸采样;
(4)14500÷10=1450(根),
答:该采样点在这周至少需要 1450 根采样管.
24.【解答】解:(1)设每个 A 类礼盒的售价为 x 元,每个 B 类礼盒的售价为 y 元,
根据题意得: ,
解得: .
答:每个 A 类礼盒的售价为 160 元.
(2)∵240×0.9=216(元),216>200,
∴每个 B 类礼盒的活动价为(216﹣2a)元.
根据题意得:(160﹣a﹣120)×800+(216﹣2a﹣160)×1000=48800,
解得:a=14.
答:a 的值为 14.
25.【解答】解:(1)探究一:
如图 1,当 n=0 时,图中线段有 1 条,
如图 2,当 n=1 时,图中线段有 2+1=3 条,
如图 3,当 n=2 时,图中线段有 3+2+1=6 条,
同理,当 n=3 时,图中线段有 4+3+2+1=10 条,
,
当随机设置了 n 个点后,一共有 n+1+n+n﹣1+ +3+2+1= 条线段,
故答案为: ;
(2)探究二:
如图 4﹣1,当 m=0,n=0 时,图中一共有 1 个长方形,
如图 4﹣2,当 m=1,n=0 时,图中一共有 2+1=3 个长方形,
如图 4﹣3,当 m=2,n=0 时,图中一共有 3+2+1=6 个长方形,
同理,当 m=3,n=0 时,图中共有 4+3+2+1=10 个长方形,
,
小结:当长方形的长上随机设置 m 个点,宽上不设置点,一共有 个长方形,
同理,当长方形的长上不设置点,宽上随机设置 n 个点,一共 个长方形;
故答案为: ; ;
如图 5﹣1,当 m=1,n=1 时,长上共形成 3 条线段,宽上共形成 3 条线段,图中一共有 3×3=9 个长方形(包
括正方形),
如图 5﹣2,当 m=1,n=2 时,长上共形成 3 条线段,宽上共形成 6 条线段,图中一共有 3×6=18 个长方形(包
括正方形),
如图 5﹣3,当 m=2,n=1 时,长上共形成 6 条线段,宽上共形成 3 条线段,图中一共有 6×3=18 个长方形(包
括正方形),
如图 5﹣4,当 m=2,n=2 时,长上共形成 6 条线段,宽上共形成 6 条线段,图中一共有 6×6=36 个长方形(包
括正方形),
小结:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,长上共形成 条线段,宽上共形
成 条线段连接各边对应的点,则图中一共有 个长方形(包括正方
形);
【问题解决】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、C、D,
且相对的边点的位置相同),如图连接各边对应的点,
则长上共形成 =465 条线段,宽上共形成 =210 条线段,图中一共有 465×
210=97650 个长方形(包括正方形),
故答案为:97650.
一、单选题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 1-8 各小题所选答案的标号涂写在答题纸规定的
位置.
1.(3 分)﹣5 的倒数是( )
A. B.﹣ C.﹣5 D.5
2.(3 分)如图,是由几个大小完全一样的小正方体搭成的几何体,该几何体从左面看的形状图是( )
A. B.
C. D.
3.(3 分)下列计算①(﹣1)×(﹣2)×(﹣3)=6;②(﹣36)÷(﹣9)=﹣4;③ ×(﹣ )÷(﹣1)
= ;④(﹣4)÷ ×(﹣2)=16.其中正确的个数( )
A.4 个 B.3 个 C.2 个 D.1 个
4.(3 分)下列调查方式中,适合采用普查方式的是( )
A.了解一批圆珠笔芯的使用寿命
B.调查市民对“地铁 1 号线”车站环境的意见
C.调查本市七年级学生的课业负担
D.了解一沓钞票中有没有假钞
5.(3 分)下列各题运算正确的是( )
3 3 6 3 3
A.5a +3a =8a B.3a ﹣2a =1
3 3 3 3 3
C.4a ﹣3a =a D.﹣4a +3a =﹣a
6.(3分)在如图的 2022年 6月份的月历表中,任意框出表中同一竖列上三个相邻的数,这三个数的和不可能是( )
A.27 B.51 C.75 D.69
7.(3 分)有理数 a、b、c 在数轴上的对应点如图所示,化简代数式:|a﹣b|+|a+b|﹣3|c﹣a|=( )
A.﹣3c B.a﹣3c C.﹣2a﹣2b﹣3c D.﹣4a+3c
8.(3 分)为使全国人民都过上幸福的小康生活,近年来各地扶贫办致力于帮扶当地区特色产品走进市民的菜篮子,
助力更多优质农产品走出地区、走向全国.已知有一扶贫农产品去年和今年两年的销售总额为 180 万元,其中该
扶贫农产品去年的价格为 15 元/千克,今年的价格为 12 元/千克,今年的销售产量比去年增长了 25%.今年该扶
贫农产品销售( )千克.
A.60000 B.75000 C.6000 D.7500
二、填空题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 9-16 各小题的答案填写在答题纸规定的位置.
9.(3 分) 的系数是 .
10.(3 分)我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地
位,其星载原子钟的精度,已经提升到了每 3000000 年误差 1 秒.数 3000000 用科学记数法表示为 .
a+2 2 5 b b
11.(3 分)如果单项式 x y 与 2x y 是同类项,那么 a = .
3 2 3
12.(3 分)化简:(6a ﹣a ﹣4a﹣3)﹣(3a ﹣2a+1)= .
13.(3 分)如图,∠AOB 是直角,∠BOC=36°,OD 平分∠AOC,则∠BOD= °.
14.(3 分)一个两位数,十位数字是个位数字的 3 倍,将两个数字对调后得到的新两位数比原来的两位数小 36,
原来两位数是 .
15.(3 分)将一个底面直径是 10 厘米、高为 60 厘米的圆柱锻压成底面直径为 30 厘米的圆柱,则锻压后圆柱的高
为 厘米.
16.(3 分)卡塔尔世界杯吸引了很多球迷的观看.某观看大厅观众区分为三部分,中间部分为固定座位数,每排
13 座,两边成扇形,第一排两边都为 5 座,第二排两边都为 7 座,第三排两边都为 9 座,往后按照此规律依次
类推 若此演出大厅共有 15 排座位,则能同时容纳 人观看.
三、作图题(本题满分 4 分)尺规作图,不写作法,保留作图痕迹.
17.(4 分)已知:线段 a、b,求作:线段 AB,使 AB=3b﹣a.
四、解答题(本题共有 8 道小题,满分 68 分)
18.(12 分)计算与化简求值
(1) ;
3 2
(2) ﹣[(﹣3 )﹣4 ];
3 2 3 2
(3)先化简再求值:﹣ (3x +6x +18)+ (x ﹣4x +4),其中 x=﹣ .
19.(8 分)解方程
(1) x=﹣1;
(2) =3(x﹣4).
20.(6 分)已知:线段 AB=20cm,点 C、D 为线段 AB 上两点,且 BC= AB,AD= AB,点 M 和点 N 分别是
线段 AC 和 BD 的中点.求:线段 MN 的长.
21.(6 分)已知:∠COD 在∠AOB 的内部,且∠AOB=160°,∠COD= ∠AOB,射线 OE 平分∠AOD,∠COE
=18°.
求:(1)∠AOD 的度数;
(2)∠BOC 的度数.
22.(8 分)我区某学校组织开展了疫情防控知识的培训.为了解学生们对疫情防控知识的学习情况,学校准备采用
以下调查方式中的一种进行调查:
①从七年级一班随机选取 20 名学生作为调查对象进行调查;
②从八年级中随机选取 300 名学生作为调查对象进行调查;
③从全校学生学籍档案中随机抽取 300 名学生作为调查对象进行调查.
按照一种比较合理的调查方式所得到的数据后,学校按成绩分成五个等级,并绘制了如下不完整的统计图
等级 成绩
A 50≤x<
60
B 60≤x<
70
C 70≤x<
80
D 80≤x<
90
E 90≤x≤
100
(1)在上述调查方式中,你认为比较合理的一个是 (填序号);
(2)在学生成绩频数分布直方图中 m 的值为 人;
(3)在学生成绩扇形统计图中,D 项所在的圆心角的度数为 °;
(4)若成绩在 80 分及以上为优秀,全校共有 1800 名学生,估计成绩优秀的学生有多少人?
23.(8 分)为常态化开展社会人群核酸检测工作,我区在人群密集、流动量大的区域布局了健康小屋(便民核酸采
样点).某采样点计划每天完成 2000 人次的核酸采样,实际每天采样的数量相比有出入,如表是十二月份某一周
该采样点的实际采样人次(超过为正,不足为负,单位:人次)
星期 一 二 三 四 五 六 七
增减 +150 ﹣250 +400 ﹣100 +150 +200 +150
(1)根据记录可知该采样点前三天共完成了多少人次的核酸采样?
(2)采样人次最多的一天比采样人次最少的一天多了多少人次?
(3)该采样点采用十人混检的方式收集核酸样本(将 10 个人的样本采集后放到同一根采样管中进行检测),该
采样点这周平均每天完成多少人次的核酸采样?
(4)该采样点在这周至少需要多少根采样管?
24.(10 分)为喜迎元旦,某超市推出 A 类礼盒和 B 类礼盒,每个 A 类礼盒的成本为 120 元,每个 B 类礼盒的成本
为 160 元,每个 B 类礼盒的售价比每个 A 类礼盒的售价多 80 元,售卖 2 个 A 类礼盒获得的利润和售卖 1 个 B 类
礼盒获得的利润相同.
(1)求每个 A 类礼盒的售价;
(2)该超市购进 A 类礼盒 800 个和 B 类礼盒 1000 个,进行促销活动.超市规定,每人每次最多购买 A 类礼盒
1 个或 B 类礼盒 1 个,每个 A 类礼盒直接参与店内“每满 100 元减 a 元”的活动,每个 B 类礼盒在售价的基础
上打九折后再参与店内“每满 100 元减 a 元”的活动.活动结束时,所有礼盒全部售卖完.若该超市获得的利润
为 48800 元,求 a 的值.
25.(10 分)【问题提出】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、
C、D,且相对的边点的位置相同),如图连接各边对应的点,则图中一共有多少个长方形(包括正方形)?
【问题探究】:为解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:
(1)探究一:将一条线段上随机设置 n 个点,图中一共可以形成多少条线段?
如图 1,当 n=0 时,图中线段有:线段 AB,共 1 条线段;
如图 2,当 n=1 时,以 A 为端点的线段有:线段 AC 和线段 AB,共 2 条线段;以 C 为端点的有:线段 CB,共
1 条线段,故图中共有 2+1=3 条线段;
如图 3,当 n=2 时,以 A 为端点的线段有:线段 AC,线段 AD 和线段 AB,共 3 条线段;以 C 为端点的有:线
段 CD 和线段 CB,共 2 条线段;以 D 为端点的有:线段 DB,共 1 条线段,故图中共有 3+2+1=6 条线段;
小结:当随机设置了 n 个点后,一共可以形成 条线段.(用含 n 的代数式表示)
(2)探究二:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,则一共有多少个长方形(包括正方形)?
首先我们先探究宽上不设置点的情况.
如图 4﹣1,当 m=0,n=0 时,图中一共有 1 个长方形.
如图 4﹣2,当 m=1,n=0 时,图中一共有 3 个长方形.
如图 4﹣3,当 m=2,n=0 时,图中一共有 6 个长方形.
小结:当长方形的长上随机设置 m 个点,宽上不设置点,一共有 个长方形.(用含 m 的代数式表示)
同理,当长方形的长上不设置点,宽上随机设置 n 个点,一共有 个长方形.(用含 n 的代数式表示)
如图 5﹣1,当 m=1,n=1 时,长上共形成 3 条线段,宽上共形成 3 条线段,图中一共有 9 个长方形(包括正方
形).
如图 5﹣2,当 m=1,n=2 时,长上共形成 3 条线段,宽上共形成 6 条线段,图中一共有 18 个长方形(包括正
方形).
如图 5﹣3,当 m=2,n=1 时,长上共形成 6 条线段,宽上共形成 3 条线段,图中一共有 18 个长方形(包括正
方形).
如图 5﹣4,当 m=2,n=2 时,长上共形成 6 条线段,宽上共形成 6 条线段,图中一共有 36 个长方形(包括正
方形).
小结:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,连接各边对应的点,则图中一共有 个
长方形(包括正方形).(用含 m、n 的代数式表示)
【问题解决】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、C、D,
且相对的边点的位置相同),如图连接各边对应的点,则图中一共有 个长方形(包括正方形).(直接写
出最后计算结果)
2022-2023 学年山东省青岛市城阳区七年级(上)期末数学试卷
参考答案与试题解析
一、单选题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 1-8 各小题所选答案的标号涂写在答题纸规定的
位置.
1.【解答】解:∵(﹣5)×(﹣ )=1,
∴﹣5 的倒数是﹣ .
故选:B.
2.【解答】解:从左边看,底层是两个小正方形,上层的左边是一个小正方形,
故选:B.
3.【解答】解:①(﹣1)×(﹣2)×(﹣3)=﹣6,故原题计算错误;
②(﹣36)÷(﹣9)=4,故原题计算错误;
③ ×(﹣ )÷(﹣1)= ,故原题计算正确;
④(﹣4)÷ ×(﹣2)=16,故原题计算正确,
正确的计算有 2 个,
故选:C.
4.【解答】解:A、了解一批圆珠笔芯的使用寿命,适合采用抽样调查方式,不符合题意;
B、调查市民对“地铁 1 号线”车站环境的意见,适合采用抽样调查方式,不符合题意;
C、调查本市七年级学生的课业负担,适合采用抽样调查方式,不符合题意;
D、了解一沓钞票中有没有假钞,适合采用普查方式,符合题意;
故选:D.
3 3 3
5.【解答】解:A、5a +3a =8a ,原计算错误,故此选项不符合题意;
3 3 3
B、3a ﹣2a =2a ,原计算错误,故此选项不符合题意;
3 3 3
C、4a ﹣3a =a ,原计算错误,故此选项不符合题意;
3 3 3
D、﹣4a +3a =﹣a ,原计算正确,故此选项符合题意.
故选:D.
6.【解答】解:设框出的最小数是 x,则另外两个数是 x+7,x+14,
这三个数的和是 x+x+7+x+14=3x+21,
若 3x+21=27,则 x=2,框出的三个数是 2,9,16,故 A 不符合题意;
若 3x+21=51,则 x=10,框出的三个数是 10,17,24,故 B 不符合题意;
若 3x+21=75,则 x=18,框出的三个数是 18,25,32,
从图可知不能框出 18,25,32,故 C 符合题意;
若 3x+21=69,则 x=16,框出的三个数是 16,23,30,故 D 不符合题意;
故选:C.
7.【解答】解:根据数轴上点的位置得:a<b<0<c,
∴a﹣b<0,a+b<0,c﹣a>0,
则原式=b﹣a﹣a﹣b﹣3c+3a=a﹣3c,
故选:B.
8.【解答】解:设去年该扶贫农产品销售 x 千克,则今年该扶贫农产品销售(1+25%)x 千克,
根据题意得:15x+12×(1+25%)x=1800000,
解得 x=60000,
∴(1+25%)x=75000,
∴今年该扶贫农产品销售 75000 千克,
故选:B.
二、填空题(本题满分 24 分,共有 8 道小题,每小题 3 分)请将 9-16 各小题的答案填写在答题纸规定的位置.
9.【解答】解: 的系数是﹣ .
故答案为:﹣ .
6
10.【解答】解:数 3000000 用科学记数法表示为 3×10 ,
6
故答案为:3×10 .
a+2 2 5 b
11.【解答】解:∵单项式 x y 与 2x y 是同类项,
∴a+2=5,b=2,
∴a=3,
b 2
∴a =3 =9.
故答案为:9.
3 2 3
12.【解答】解:(6a ﹣a ﹣4a﹣3)﹣(3a ﹣2a+1)
3 2 3
=6a ﹣a ﹣4a﹣3﹣3a +2a﹣1
3 2
=3a ﹣a ﹣2a﹣4,
3 2
故答案为:3a ﹣a ﹣2a﹣4.
13.【解答】解:∵∠AOB 是直角,∠BOC=36°,
∴∠AOC=90°+36°=126°,
∵OD 平分∠AOC,
∴∠COD= ∠AOC=63°,
∴∠BOD=∠COD﹣∠BOC=63°﹣36°=27°,
故答案为:27.
14.【解答】解:设原来两位数的个位数字是 x,则它的十位数字是 3x,
根据题意得 10×3x+x﹣(10x+3x)=36,
解得 x=2,
所以 3x=6,
所以原来的两位是 62,
故答案为:62.
15.【解答】解:设锻压后圆柱的高为 x 厘米,由题意得:
2 2
π( ) x=π( ) ×60,
解得:x= .
答:锻压后圆柱的高为 厘米.
故答案为: .
16.【解答】解:根据题意有,
5+(15﹣1)×2=5+28=33
两边部分的座位数为:2×(5+7+9+...+33)=2× =570(座),
中间部分的座位数为:13×15=195(座),
195+570=765(座),
∴能同时容纳 765 人观看.
故答案为:765
三、作图题(本题满分 4 分)尺规作图,不写作法,保留作图痕迹.
17.【解答】解:如图:
AB 即为所求.
四、解答题(本题共有 8 道小题,满分 68 分)
18.【解答】解:(1)原式=﹣8×(﹣2+ ﹣ )
=﹣2×(﹣8)+ ×(﹣8)﹣ ×(﹣8)
=16﹣4+1
=12+1
=13.
(2)原式=5÷(﹣ )﹣(﹣27﹣16)
=﹣60﹣(﹣43)
=﹣60+43
=﹣17.
3 2 3 2
(3)原式=﹣ x ﹣x ﹣3+ x ﹣2x +2
2
=﹣3x ﹣1,
当 x=﹣ 时,
原式=﹣3× ﹣1
=﹣ ﹣1
= .
19.【解答】解:(1)去分母得:4(x﹣5)﹣3x=﹣12,
去括号得:4x﹣20﹣3x=﹣12,
解得:x=8;
(2)去括号得:x﹣2x﹣1=3x﹣12,
移项得:x﹣2x﹣3x=﹣12+1,
合并得:﹣4x=﹣11,
解得:x= .
20.【解答】解:∵AB=20cm,BC= AB,AD= AB,
∴BC=4cm,AD=5cm,
∴AC=AB﹣BC=16cm,BD=AB﹣AD=15cm,
∵M、N 分别是线段 AC、BD 的中点,
∴AM=CM= AC=8cm,BN=DN= BD= cm,
∴MN=AB﹣AM﹣BN=20cm﹣8cm﹣ cm= cm.
21.【解答】解:(1)∵∠AOB=160°,∠COE=18°,
∴∠COD= ∠AOB ×160°=40°,
∴∠EOD=∠EOC+∠COD=18°+40°=58°,
∵射线 OE 平分∠AOD,
∴∠AOE=∠EOD= ∠AOD,
∴∠AOD=2∠EOD=2×58°=116°;
∴∠AOD 的度数为 116°;
(2)由(1)得∠AOE=∠EOD=58°,
∵∠COE=18°,∠AOB=160°,
∴∠AOC=∠AOE+∠COE=58°+18°=76°,
∴∠BOC=∠AOB﹣∠AOC=160°﹣76°=84°.
∴∠BOC 的度数为 84°.
22.【解答】解:(1)由题意可得,从全校学生学籍档案中随机抽取 300 名学生作为调查对象进行调查,比较合理,
故答案为:③;
(2)60÷30%=200(人),
m=200×9%=18,
故答案为:18;
(3)360°× =144°,
故答案为:144;
(4)1800× =936(人),
答:估计成绩优秀的学生有 936 人.
23.【解答】解:(1)[+100+(﹣250)+(+400)]+2000×3
=250+6000
=6250(人次),
答:该采样点前三天共完成了 6250 人次的核酸采样;
(2)+400﹣(﹣250)=400+250=650(人次),
答:采样人次最多的一天比采样人次最少的一天多了 650 人次;
(3)(100﹣250+400﹣250﹣100+350+150)+2000×7
=500+14000
=14500(人次),
答:该采样点这周平均每天完成 14500 人次的核酸采样;
(4)14500÷10=1450(根),
答:该采样点在这周至少需要 1450 根采样管.
24.【解答】解:(1)设每个 A 类礼盒的售价为 x 元,每个 B 类礼盒的售价为 y 元,
根据题意得: ,
解得: .
答:每个 A 类礼盒的售价为 160 元.
(2)∵240×0.9=216(元),216>200,
∴每个 B 类礼盒的活动价为(216﹣2a)元.
根据题意得:(160﹣a﹣120)×800+(216﹣2a﹣160)×1000=48800,
解得:a=14.
答:a 的值为 14.
25.【解答】解:(1)探究一:
如图 1,当 n=0 时,图中线段有 1 条,
如图 2,当 n=1 时,图中线段有 2+1=3 条,
如图 3,当 n=2 时,图中线段有 3+2+1=6 条,
同理,当 n=3 时,图中线段有 4+3+2+1=10 条,
,
当随机设置了 n 个点后,一共有 n+1+n+n﹣1+ +3+2+1= 条线段,
故答案为: ;
(2)探究二:
如图 4﹣1,当 m=0,n=0 时,图中一共有 1 个长方形,
如图 4﹣2,当 m=1,n=0 时,图中一共有 2+1=3 个长方形,
如图 4﹣3,当 m=2,n=0 时,图中一共有 3+2+1=6 个长方形,
同理,当 m=3,n=0 时,图中共有 4+3+2+1=10 个长方形,
,
小结:当长方形的长上随机设置 m 个点,宽上不设置点,一共有 个长方形,
同理,当长方形的长上不设置点,宽上随机设置 n 个点,一共 个长方形;
故答案为: ; ;
如图 5﹣1,当 m=1,n=1 时,长上共形成 3 条线段,宽上共形成 3 条线段,图中一共有 3×3=9 个长方形(包
括正方形),
如图 5﹣2,当 m=1,n=2 时,长上共形成 3 条线段,宽上共形成 6 条线段,图中一共有 3×6=18 个长方形(包
括正方形),
如图 5﹣3,当 m=2,n=1 时,长上共形成 6 条线段,宽上共形成 3 条线段,图中一共有 6×3=18 个长方形(包
括正方形),
如图 5﹣4,当 m=2,n=2 时,长上共形成 6 条线段,宽上共形成 6 条线段,图中一共有 6×6=36 个长方形(包
括正方形),
小结:将长方形的长上随机设置 m 个点,宽上随机设置 n 个点,长上共形成 条线段,宽上共形
成 条线段连接各边对应的点,则图中一共有 个长方形(包括正方
形);
【问题解决】:将长方形的长上随机设置 29 个点,宽上随机设置 19 个点(不含长方形的各顶点 A、B、C、D,
且相对的边点的位置相同),如图连接各边对应的点,
则长上共形成 =465 条线段,宽上共形成 =210 条线段,图中一共有 465×
210=97650 个长方形(包括正方形),
故答案为:97650.
同课章节目录
