24.1 旋转(4)课件 (共25张PPT)
文档属性
| 名称 | 24.1 旋转(4)课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
沪科版 九年级下册
24.1旋转(4)
课件说明
教学目标: 1.理解点 P 与点 P′关于原点对称时,它们的横纵 坐标的关系; 2.会用关于原点对称的点的坐标的关系解决有关问 题.
教学重点: 点 P(x,y)关于原点的对称点 P (-x,-y)及其应用.
′
关于y 轴对称的点的纵坐标相等,
横坐标互为相反数.
关于x 轴对称的点的横坐标相同,
纵坐标互为相反数.
点(x,y)关于x 轴对称的点的坐标为(__,___);
点(x,y)关于y 轴对称的点的坐标为(___,__).
x -y
-x y
复习旧知
关于坐标轴对称的点的坐标的特征
1.(1)点 M(2,-3)关于 x 轴对称的点的坐标为 ,点 M 到 x 轴的距离为 ,
点 M 到y轴的距离为 ;
(2)点 N(-3,-2)关于 y 轴对称的点的坐标为 ,点 N 到 x 轴的距离为 ,
点N到y 轴的距离为 .
(2,3)
3
2
(3,-2)
2
3
复习旧知
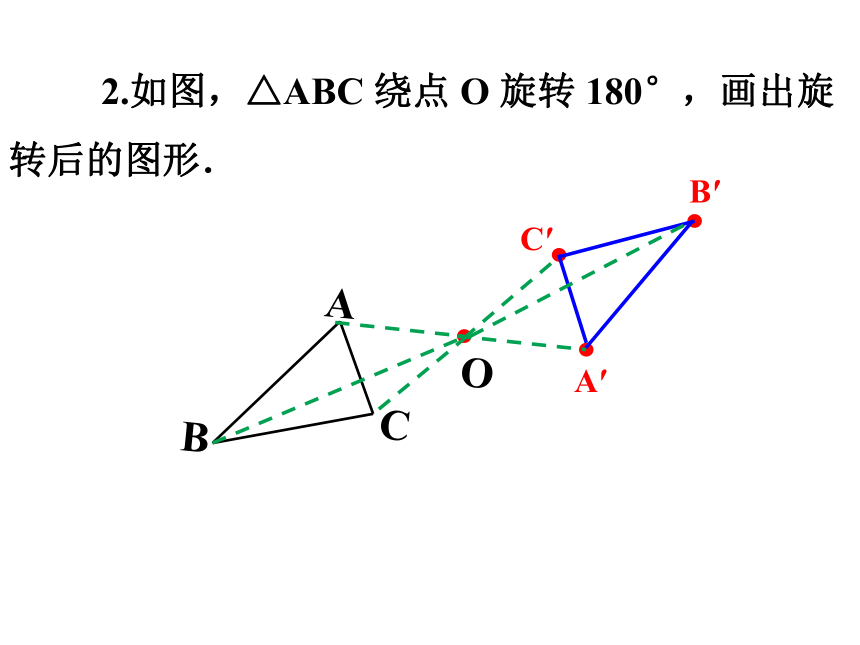
2.如图,△ABC 绕点 O 旋转 180°,画出旋转后的图形.
A
B
C
O
A′
B′
C′
图形在平面直角坐标系中的旋转:
在平面直角坐标系中,把一个图形以原点O为旋转中心作几个特殊角度的旋转,可得如下结果.
原图形上任一 点的坐标 以原点0为旋转中心按逆时针方向旋转后对应 点坐标
旋转
90° 旋转
180° 旋转
270° 旋转
360°
(x,y) ( ,) ( ,) ( , ) ( ,)
学习新知
在平面直角坐标系中画出点 A(1,2),B(2,0),C(-3,1), D (-2,-1), E (0,-3),并画出这些点关于原点成中心对称的对应点,写出它们的坐标.这些坐标与已知点的坐标有什么关系?
探究新知
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
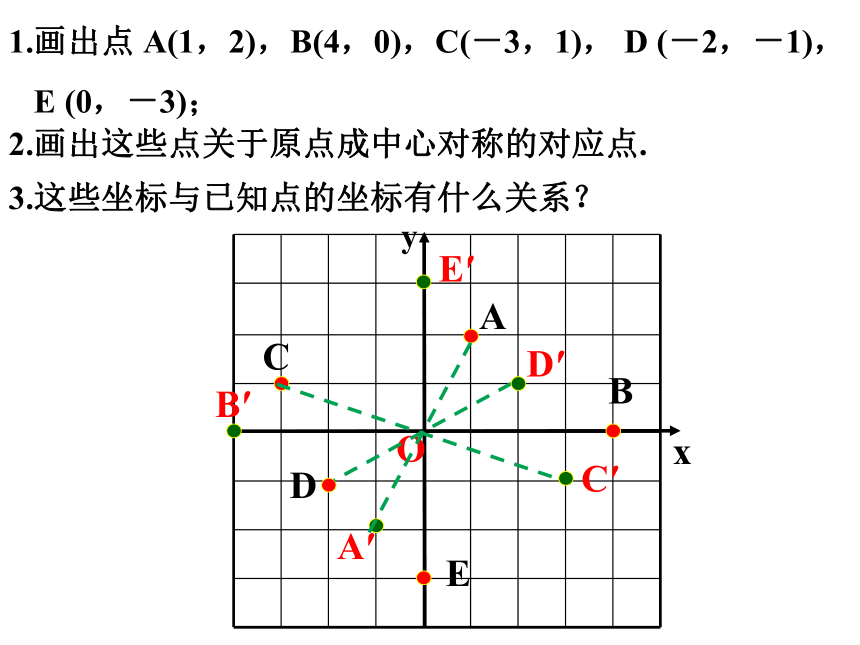
1.画出点 A(1,2),B(4,0),C(-3,1), D (-2,-1),
E (0,-3);
2.画出这些点关于原点成中心对称的对应点.
3.这些坐标与已知点的坐标有什么关系?
(1)关于原点对称的两个点的横坐标的绝对值有什么关系?纵坐标的绝对值又有什么关系?
(2)横、纵坐标符号之间又有什么关系?
两个点关于原点对称时,它们的坐标符号相反,即点 P(x,y)关于原点 O 的对称点为 P′(-x,-y).
关于原点对称的两个点的横坐标的绝对值相等.
关于原点对称的两个点的纵坐标的绝对值相等.
1.在平面直角坐标系中,把点P(-3,2)绕原点O
顺时针旋转 180°,所得 到的对应点P'的坐标
为( ).
练习巩固
A.(3,2) B.(2, -3)
C.(-3,-2) D.(3,-2)
D
2.在平面直角坐标系中,将△AOB 绕原点O顺时
针旋转 180°后得到△A1OB1.若点B的坐标为
(-1, -2),则点B的对应点B1的坐标为( ).
A.(1,-2) B. (1,2)
C.(-1,-2) D. (2,1)
3.在平面直角坐标系中,将点A(3,4)绕 原点O
旋转180°得到点B,此时点C恰好与 点B关
于x轴对称,则点C的坐标为 .
B
(-3,4)
x
y
O
A
B
C
D
4.如图,已知口ABCD 的中心在原点O,顶点A
(3,2),D(2,-2),则顶点B的坐标为 .
(-2,2)
5.如图, 在平面直角坐标系中,已知点 A(3,2).
将△ABO 绕点O 按逆时针方向旋转180°得到
△CDO,则点C的坐标是 .
x
y
O
A
B
C
D
(-3,-2)
在平面直角坐标系下,作一个图形的中心对称图形的步骤是什么?
(1)图形的对称转化为点的对称.标出点的中心对称点.
(2)连接线段.
学习新知
x
y
O
A
B
C
如图,△ABC 的顶点坐标分别为A(1,3),B(5,0),C(5,3),利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
例题解析
A′(-1, -3)
B′(-5, 0)
C′(-5, -3)
图中的△A′ B′ C′ 为所求.
如图所示,利用关于原点对称的点的坐标的特点,作出□ABCD 关于原点对称的图形.
x
y
O
A
B
C
A′
B′
C′
(-4,1)
(-1,1)
(-2,3)
(4,-1)
(1,-1)
(2,-3)
学以致用
D′
D
(1,3)
(-1,-3)
图中的□ A′ B′ C′D′为所求.
1.平移、轴对称和旋转有什么区别与联系? 2.旋转和中心对称有什么区别与联系? 3.怎样利用旋转的定义和性质作图?
课堂小结
1.点A(4,2)经过某种图形变换后得到点
B(-2,4),这种图形变换可以是( ).
A.关于x 轴对称
B.关于y轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°
练习巩固
C
2.如图,Rt△ABO的点A的坐标是(3,2),
将△ABO绕原点O按逆时针方向旋转90°,得到△A′B′O ,则点A的对应点 A′的坐标是 .
A
(3,2)
B
O
A′
B′
x
y
(-2,3)
3.如图,在平面直角坐标系中, Rt△ABC的直角
顶点C的坐标为(1,0);点A在轴正半轴上,且
AC=2.将△ABC先绕点C逆时针旋转90°,再
向左平移3个单位,则变换后点A的对应点的
坐标为 .
A
(1,0)
C
O
x
y
(-2, 2)
A
y
x
B
O
C
4.如图 ,在平面直角坐标系中,点A与点B 的坐
标分别为(2,0), (0,1).AC由AB绕点A顺时
针旋转90°而得,则AC所在直线的函数表达
式是 .
(3 ,2)
(2 ,0)
2k+b=0
3k+b=2
k=2
b=-4
y=2x-4
5.如下图,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,若原来点A坐标是(m,n),则经过第2023次变换后所得的点A坐标是 .
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
第1次
关于x轴对称
第2次
关于原点对称
第3次
关于y轴对称
第4次
关于x轴对称
…
A
(m, -n)
今天作业
课本P11页第6、7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.1旋转(4)
课件说明
教学目标: 1.理解点 P 与点 P′关于原点对称时,它们的横纵 坐标的关系; 2.会用关于原点对称的点的坐标的关系解决有关问 题.
教学重点: 点 P(x,y)关于原点的对称点 P (-x,-y)及其应用.
′
关于y 轴对称的点的纵坐标相等,
横坐标互为相反数.
关于x 轴对称的点的横坐标相同,
纵坐标互为相反数.
点(x,y)关于x 轴对称的点的坐标为(__,___);
点(x,y)关于y 轴对称的点的坐标为(___,__).
x -y
-x y
复习旧知
关于坐标轴对称的点的坐标的特征
1.(1)点 M(2,-3)关于 x 轴对称的点的坐标为 ,点 M 到 x 轴的距离为 ,
点 M 到y轴的距离为 ;
(2)点 N(-3,-2)关于 y 轴对称的点的坐标为 ,点 N 到 x 轴的距离为 ,
点N到y 轴的距离为 .
(2,3)
3
2
(3,-2)
2
3
复习旧知
2.如图,△ABC 绕点 O 旋转 180°,画出旋转后的图形.
A
B
C
O
A′
B′
C′
图形在平面直角坐标系中的旋转:
在平面直角坐标系中,把一个图形以原点O为旋转中心作几个特殊角度的旋转,可得如下结果.
原图形上任一 点的坐标 以原点0为旋转中心按逆时针方向旋转后对应 点坐标
旋转
90° 旋转
180° 旋转
270° 旋转
360°
(x,y) ( ,) ( ,) ( , ) ( ,)
学习新知
在平面直角坐标系中画出点 A(1,2),B(2,0),C(-3,1), D (-2,-1), E (0,-3),并画出这些点关于原点成中心对称的对应点,写出它们的坐标.这些坐标与已知点的坐标有什么关系?
探究新知
x
y
O
A
B
C
D
E
A′
B′
C′
D′
E′
1.画出点 A(1,2),B(4,0),C(-3,1), D (-2,-1),
E (0,-3);
2.画出这些点关于原点成中心对称的对应点.
3.这些坐标与已知点的坐标有什么关系?
(1)关于原点对称的两个点的横坐标的绝对值有什么关系?纵坐标的绝对值又有什么关系?
(2)横、纵坐标符号之间又有什么关系?
两个点关于原点对称时,它们的坐标符号相反,即点 P(x,y)关于原点 O 的对称点为 P′(-x,-y).
关于原点对称的两个点的横坐标的绝对值相等.
关于原点对称的两个点的纵坐标的绝对值相等.
1.在平面直角坐标系中,把点P(-3,2)绕原点O
顺时针旋转 180°,所得 到的对应点P'的坐标
为( ).
练习巩固
A.(3,2) B.(2, -3)
C.(-3,-2) D.(3,-2)
D
2.在平面直角坐标系中,将△AOB 绕原点O顺时
针旋转 180°后得到△A1OB1.若点B的坐标为
(-1, -2),则点B的对应点B1的坐标为( ).
A.(1,-2) B. (1,2)
C.(-1,-2) D. (2,1)
3.在平面直角坐标系中,将点A(3,4)绕 原点O
旋转180°得到点B,此时点C恰好与 点B关
于x轴对称,则点C的坐标为 .
B
(-3,4)
x
y
O
A
B
C
D
4.如图,已知口ABCD 的中心在原点O,顶点A
(3,2),D(2,-2),则顶点B的坐标为 .
(-2,2)
5.如图, 在平面直角坐标系中,已知点 A(3,2).
将△ABO 绕点O 按逆时针方向旋转180°得到
△CDO,则点C的坐标是 .
x
y
O
A
B
C
D
(-3,-2)
在平面直角坐标系下,作一个图形的中心对称图形的步骤是什么?
(1)图形的对称转化为点的对称.标出点的中心对称点.
(2)连接线段.
学习新知
x
y
O
A
B
C
如图,△ABC 的顶点坐标分别为A(1,3),B(5,0),C(5,3),利用关于原点对称的点的坐标的特点,作出△ABC关于原点对称的图形.
例题解析
A′(-1, -3)
B′(-5, 0)
C′(-5, -3)
图中的△A′ B′ C′ 为所求.
如图所示,利用关于原点对称的点的坐标的特点,作出□ABCD 关于原点对称的图形.
x
y
O
A
B
C
A′
B′
C′
(-4,1)
(-1,1)
(-2,3)
(4,-1)
(1,-1)
(2,-3)
学以致用
D′
D
(1,3)
(-1,-3)
图中的□ A′ B′ C′D′为所求.
1.平移、轴对称和旋转有什么区别与联系? 2.旋转和中心对称有什么区别与联系? 3.怎样利用旋转的定义和性质作图?
课堂小结
1.点A(4,2)经过某种图形变换后得到点
B(-2,4),这种图形变换可以是( ).
A.关于x 轴对称
B.关于y轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°
练习巩固
C
2.如图,Rt△ABO的点A的坐标是(3,2),
将△ABO绕原点O按逆时针方向旋转90°,得到△A′B′O ,则点A的对应点 A′的坐标是 .
A
(3,2)
B
O
A′
B′
x
y
(-2,3)
3.如图,在平面直角坐标系中, Rt△ABC的直角
顶点C的坐标为(1,0);点A在轴正半轴上,且
AC=2.将△ABC先绕点C逆时针旋转90°,再
向左平移3个单位,则变换后点A的对应点的
坐标为 .
A
(1,0)
C
O
x
y
(-2, 2)
A
y
x
B
O
C
4.如图 ,在平面直角坐标系中,点A与点B 的坐
标分别为(2,0), (0,1).AC由AB绕点A顺时
针旋转90°而得,则AC所在直线的函数表达
式是 .
(3 ,2)
(2 ,0)
2k+b=0
3k+b=2
k=2
b=-4
y=2x-4
5.如下图,在平面直角坐标系中,对△ABC进行循环往复的轴对称或中心对称变换,若原来点A坐标是(m,n),则经过第2023次变换后所得的点A坐标是 .
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
第1次
关于x轴对称
第2次
关于原点对称
第3次
关于y轴对称
第4次
关于x轴对称
…
A
(m, -n)
今天作业
课本P11页第6、7、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
