24.4 直线与圆的位置关系(2)课件 (共25张PPT)
文档属性
| 名称 | 24.4 直线与圆的位置关系(2)课件 (共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 19:32:39 | ||
图片预览







文档简介
(共25张PPT)
沪科版 九年级下册
24.4直线与圆的位置关系(2)
教学目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
教学重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
相切
相交
相离
①直线和圆有唯一的公共点;
②圆心到直线的距离和圆的半径相等.
复习旧知
1.已知⊙O 的直径为2 cm,圆心O到直 线l的距
离为1cm,则直线l与⊙O的位置关系是( ).
A.相交 B. 相切 C.相离 D. 无法确定
2.已知平面内有⊙O和点A,B,若⊙O半径为
2cm,线段OA=3cm,OB=2cm,则直线AB
与⊙O 的位置关系为 ( ).
A.相离 B.相交 C. 相切 D.相交或相切
B
D
3.在平面直角坐标系中, ⊙P 的圆心P的坐标为
(-2,4),半径为3,则圆心P到x轴的距离
是 , ⊙P与x轴的位置关系是 ,
圆心P到y轴的距离是 , ⊙P与y轴的位
置关系是 .
4
相离
2
相交
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
O
P
作法
1.连接OP
2.过点P作直线L ⊥OP
则直线L为所求
L
学习新知
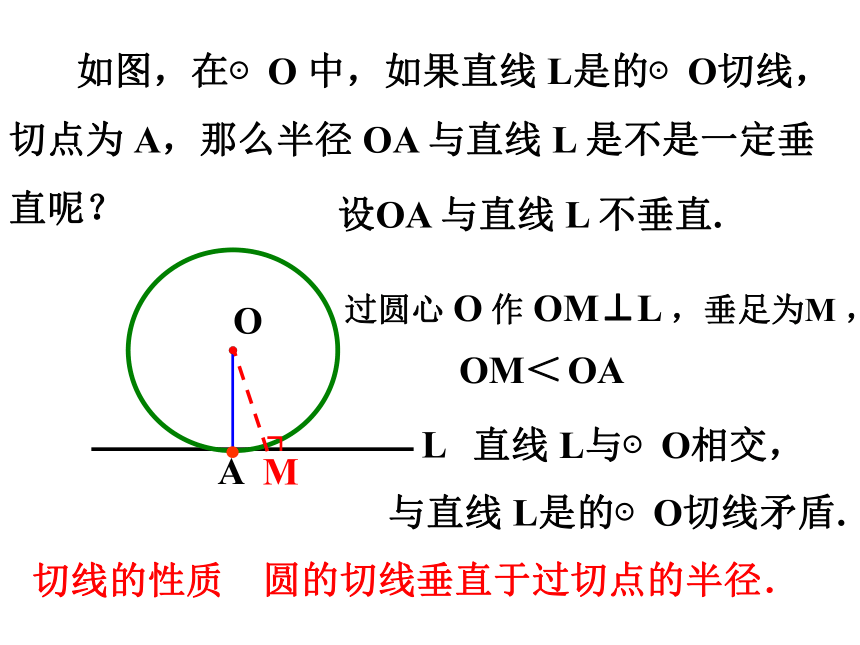
如图,在⊙O 中,如果直线 L是的⊙O切线,切点为 A,那么半径 OA 与直线 L 是不是一定垂直呢?
圆的切线垂直于过切点的半径.
L
O
A
M
OA
OM<
设OA 与直线 L 不垂直.
过圆心 O 作 OM⊥L ,垂足为M ,
直线 L与⊙O相交,
与直线 L是的⊙O切线矛盾.
切线的性质
如图,在⊙O中,经过半径 OA 的外端点 A 作直线L⊥OA,则圆心 O 到直线 L的距离是多少?直线 L和⊙O有什么位置关系?
经过半径的外端并且垂直于
这条半径的直线是圆的切线.
L
O
A
圆心 O 到直线 L的距离
等于半径OA
相切
切线的判定
下面图中直线 L 与圆相切吗?
L
O
A
L
O
A
×
×
下雨天,当你快速转动雨伞时,飞出的水珠,存在与圆相切的现象.
在砂轮上打磨工件时,飞出的火星中,
存在与圆相切的现象.
生活中圆相切的现象.
例3 已知:如图,∠ABC=45° ,AB是⊙O的直径,AB=AC. 求证:AC是⊙O的切线.
证明:
∵ AB=AC,
∴ ∠ACB=∠ABC=45°.
∴∠BAC=180°-∠ABC-∠ACB
∴ AC是⊙O的切线.
∵ AB是⊙O 的直径 ,
∵∠ABC=45°,
∴ ∠ACB=∠ABC.
=180°-45°-45°
=90°.
O
A
B
C
∴ AC⊥OA.
例题解析
已知:如图,直线AB过⊙O上的点C,且OA=OB,CA=CB. 求证:AB是⊙O的切线.
证明:
∵ OA=OB,
∴ AB是⊙O的切线.
∵点C在⊙O 上 ,
CA=CB ,
∴ OC ⊥ AB.
O
A
B
C
连接OC.
连半径,证垂直.
练习巩固
已知:如图,在△ABC 中,AB=AC,O为BC的中点,AC与⊙O相切于点D.
证明:
∵ AB=AC,
OB=OC ,
O
A
B
C
连接OD,
D
OA,
过圆心 O 作 OE⊥AB ,垂足为E ,
求证:AB是⊙O的切线.
E
∴∠BAO=∠CAO.
∴OD⊥AC.
∵AB 与⊙O 相切于点 D,
∵OE⊥AB,
∴OE=OD,
∴AB是⊙O 的切线.
作垂线,证半径.
例题解析
如果直线与圆有交点,则连接交点与圆心得半径,证这 条半径与该直线垂直.
当直线与圆的交点个数或交点的位置不明确时,则过圆心作直线的垂线,然后证圆心到直线的距离等于圆的半径.
判定圆的切线的两种思路:
O
A
B
C
O
A
B
C
D
思路1:
概括为:连半径,证垂直.
思路2:
概括为:作垂线,证半径.
1. 已知:如图,点P在∠BAC的平分线上,PD ⊥ AB,垂足为D. 求证:以点P为圆心、PD为半径的圆与∠BAC两边相切.
证明:
P
A
B
C
D
E
过点P作 PE⊥AC ,垂足为E ,
∵PE⊥AC,
PD⊥AB,
点P在∠BAC的平分线上,
∴PE=PD,
∴以点P为圆心、PD为半径的圆与∠BAC两边相切.
练习巩固
证明:
∴ DC是⊙O的切线.
O
A
B
C
D
连接OC,
BC.
∵ AB是⊙O的直径,
∴ ∠ACB=90°.
∵ ∠CAB=30°,
∴ ∠ABC=60°.
∵ OB=OC,
求证:DC是⊙O的切线.
2.已知:如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
∴ △ABC是等边三角形.
∴ BC=OB,
∵ BD=OB,
∴ ∠OBC=∠OCB=60°.
∴ BC=BD,
∴∠BCD=30°.
∴∠OCD=∠BCD+∠OCB=90°.
∴ CD⊥OC,
证明:
∴ DC是⊙O的切线.
O
A
B
C
D
连接OC,
BC.
∵ AB是⊙O的直径,
∴ ∠ACB=90°.
∵ ∠CAB=30°,
∴ ∠ABC=60°.
∵ OB=OC,
求证:DC是⊙O的切线.
2.已知:如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
∴ △ABC是等边三角形.
∴ BC=OB,
∵ BD=OB,
∴ BC=BD=OB
∴ △OCD是直角三角形.
∴ CD⊥OC,
= OD,
1
2
(1)切线的判定定理与性质定理是什么?
它们有怎样的联系?
(2)在应用切线的判定定理和性质定理时,
需要注意什么?
课堂小结
1.如图 ,AB是⊙O的直径,AC是⊙O的切线,
A为切点,若∠ C=40°,则∠ABC的度数
为( ).
A. 40° B. 50° C. 60° D.90°
O
A
B
C
B
练习巩固
2.如图 ,AB 是⊙O的直径,AC是⊙O的切线,A
为切点,BC与⊙O交于点D,连接OD.若∠ C
=50°,则∠AOD的度数为( ).
A. 40° B. 50° C. 80° D. 100°
O
A
B
C
D
C
3.如图 ,直线l是⊙O 的切线,A为切点,B为
直线l上一点,连接 OB 交⊙O于点C.若AB=4,
OA=3,则BC的长为( ) .
A. 5 B.4 C. 3 D. 2
O
A
B
C
D
4.如图 ,PA 是⊙O 的切线,切点为A,PO的延长
线交⊙O于点B.若∠ ABP=33°,则∠ P= .
O
A
B
P
5.如图,PA 是⊙O的切线,切点为A,PA= ,
∠ P=30°,则⊙O的半径为 .
O
A
P
24°
1
今天作业
课本P40页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.4直线与圆的位置关系(2)
教学目标: 1.理解切线的判定定理与性质定理; 2.会应用切线的判定定理和性质定理解决简单问题.
教学重点: 切线的判定定理和性质定理的应用.
课件说明
1.直线和圆有哪些位置关系?
2.如何判断直线和圆相切?
相切
相交
相离
①直线和圆有唯一的公共点;
②圆心到直线的距离和圆的半径相等.
复习旧知
1.已知⊙O 的直径为2 cm,圆心O到直 线l的距
离为1cm,则直线l与⊙O的位置关系是( ).
A.相交 B. 相切 C.相离 D. 无法确定
2.已知平面内有⊙O和点A,B,若⊙O半径为
2cm,线段OA=3cm,OB=2cm,则直线AB
与⊙O 的位置关系为 ( ).
A.相离 B.相交 C. 相切 D.相交或相切
B
D
3.在平面直角坐标系中, ⊙P 的圆心P的坐标为
(-2,4),半径为3,则圆心P到x轴的距离
是 , ⊙P与x轴的位置关系是 ,
圆心P到y轴的距离是 , ⊙P与y轴的位
置关系是 .
4
相离
2
相交
已知一个圆和圆上的一点,如何过这个点画出圆的切线?
O
P
作法
1.连接OP
2.过点P作直线L ⊥OP
则直线L为所求
L
学习新知
如图,在⊙O 中,如果直线 L是的⊙O切线,切点为 A,那么半径 OA 与直线 L 是不是一定垂直呢?
圆的切线垂直于过切点的半径.
L
O
A
M
OA
OM<
设OA 与直线 L 不垂直.
过圆心 O 作 OM⊥L ,垂足为M ,
直线 L与⊙O相交,
与直线 L是的⊙O切线矛盾.
切线的性质
如图,在⊙O中,经过半径 OA 的外端点 A 作直线L⊥OA,则圆心 O 到直线 L的距离是多少?直线 L和⊙O有什么位置关系?
经过半径的外端并且垂直于
这条半径的直线是圆的切线.
L
O
A
圆心 O 到直线 L的距离
等于半径OA
相切
切线的判定
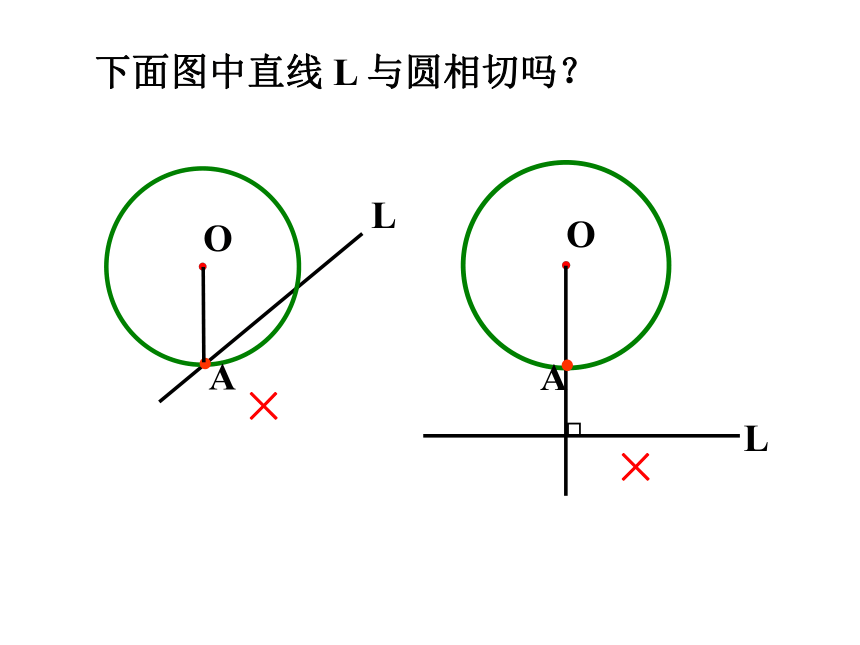
下面图中直线 L 与圆相切吗?
L
O
A
L
O
A
×
×
下雨天,当你快速转动雨伞时,飞出的水珠,存在与圆相切的现象.
在砂轮上打磨工件时,飞出的火星中,
存在与圆相切的现象.
生活中圆相切的现象.
例3 已知:如图,∠ABC=45° ,AB是⊙O的直径,AB=AC. 求证:AC是⊙O的切线.
证明:
∵ AB=AC,
∴ ∠ACB=∠ABC=45°.
∴∠BAC=180°-∠ABC-∠ACB
∴ AC是⊙O的切线.
∵ AB是⊙O 的直径 ,
∵∠ABC=45°,
∴ ∠ACB=∠ABC.
=180°-45°-45°
=90°.
O
A
B
C
∴ AC⊥OA.
例题解析
已知:如图,直线AB过⊙O上的点C,且OA=OB,CA=CB. 求证:AB是⊙O的切线.
证明:
∵ OA=OB,
∴ AB是⊙O的切线.
∵点C在⊙O 上 ,
CA=CB ,
∴ OC ⊥ AB.
O
A
B
C
连接OC.
连半径,证垂直.
练习巩固
已知:如图,在△ABC 中,AB=AC,O为BC的中点,AC与⊙O相切于点D.
证明:
∵ AB=AC,
OB=OC ,
O
A
B
C
连接OD,
D
OA,
过圆心 O 作 OE⊥AB ,垂足为E ,
求证:AB是⊙O的切线.
E
∴∠BAO=∠CAO.
∴OD⊥AC.
∵AB 与⊙O 相切于点 D,
∵OE⊥AB,
∴OE=OD,
∴AB是⊙O 的切线.
作垂线,证半径.
例题解析
如果直线与圆有交点,则连接交点与圆心得半径,证这 条半径与该直线垂直.
当直线与圆的交点个数或交点的位置不明确时,则过圆心作直线的垂线,然后证圆心到直线的距离等于圆的半径.
判定圆的切线的两种思路:
O
A
B
C
O
A
B
C
D
思路1:
概括为:连半径,证垂直.
思路2:
概括为:作垂线,证半径.
1. 已知:如图,点P在∠BAC的平分线上,PD ⊥ AB,垂足为D. 求证:以点P为圆心、PD为半径的圆与∠BAC两边相切.
证明:
P
A
B
C
D
E
过点P作 PE⊥AC ,垂足为E ,
∵PE⊥AC,
PD⊥AB,
点P在∠BAC的平分线上,
∴PE=PD,
∴以点P为圆心、PD为半径的圆与∠BAC两边相切.
练习巩固
证明:
∴ DC是⊙O的切线.
O
A
B
C
D
连接OC,
BC.
∵ AB是⊙O的直径,
∴ ∠ACB=90°.
∵ ∠CAB=30°,
∴ ∠ABC=60°.
∵ OB=OC,
求证:DC是⊙O的切线.
2.已知:如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
∴ △ABC是等边三角形.
∴ BC=OB,
∵ BD=OB,
∴ ∠OBC=∠OCB=60°.
∴ BC=BD,
∴∠BCD=30°.
∴∠OCD=∠BCD+∠OCB=90°.
∴ CD⊥OC,
证明:
∴ DC是⊙O的切线.
O
A
B
C
D
连接OC,
BC.
∵ AB是⊙O的直径,
∴ ∠ACB=90°.
∵ ∠CAB=30°,
∴ ∠ABC=60°.
∵ OB=OC,
求证:DC是⊙O的切线.
2.已知:如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在圆上,∠CAB=30°.
∴ △ABC是等边三角形.
∴ BC=OB,
∵ BD=OB,
∴ BC=BD=OB
∴ △OCD是直角三角形.
∴ CD⊥OC,
= OD,
1
2
(1)切线的判定定理与性质定理是什么?
它们有怎样的联系?
(2)在应用切线的判定定理和性质定理时,
需要注意什么?
课堂小结
1.如图 ,AB是⊙O的直径,AC是⊙O的切线,
A为切点,若∠ C=40°,则∠ABC的度数
为( ).
A. 40° B. 50° C. 60° D.90°
O
A
B
C
B
练习巩固
2.如图 ,AB 是⊙O的直径,AC是⊙O的切线,A
为切点,BC与⊙O交于点D,连接OD.若∠ C
=50°,则∠AOD的度数为( ).
A. 40° B. 50° C. 80° D. 100°
O
A
B
C
D
C
3.如图 ,直线l是⊙O 的切线,A为切点,B为
直线l上一点,连接 OB 交⊙O于点C.若AB=4,
OA=3,则BC的长为( ) .
A. 5 B.4 C. 3 D. 2
O
A
B
C
D
4.如图 ,PA 是⊙O 的切线,切点为A,PO的延长
线交⊙O于点B.若∠ ABP=33°,则∠ P= .
O
A
B
P
5.如图,PA 是⊙O的切线,切点为A,PA= ,
∠ P=30°,则⊙O的半径为 .
O
A
P
24°
1
今天作业
课本P40页第4、5、6题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
