24.5 三角形的内切圆(1)课件 (共25张PPT)
文档属性
| 名称 | 24.5 三角形的内切圆(1)课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 19:31:54 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级下册
24.5三角形的内切圆 (1)
教学目标: 1.知道三角形内切圆、内心的概念,理解切线长定 理,并会用其解决有关问题; 2.经历探究切线长定理的过程,体会应用内切圆相 关知识解决问题,渗透转化思想.
教学重点: 切线长定理及其应用.
课件说明
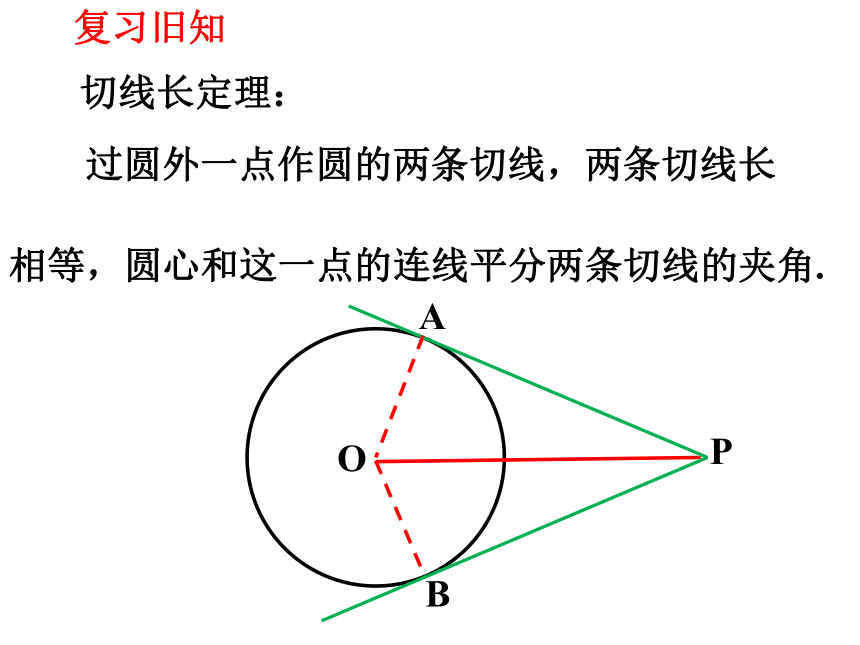
复习旧知
过圆外一点作圆的两条切线,两条切线长
相等,圆心和这一点的连线平分两条切线的夹角.
切线长定理:
O
P
A
B
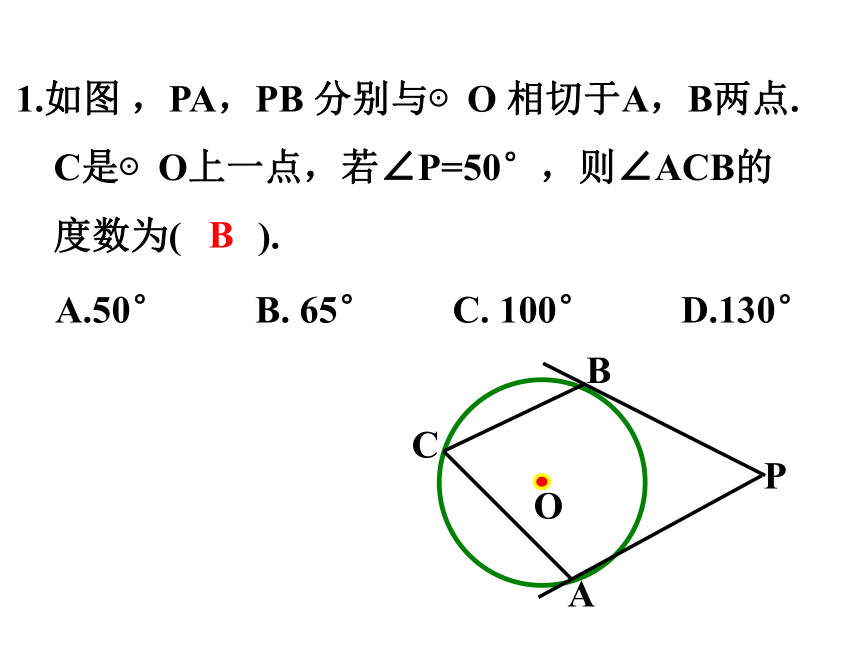
1.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
C是⊙O上一点,若∠P=50°,则∠ACB的
度数为( ).
O
A
B
P
C
A.50° B. 65° C. 100° D.130°
B
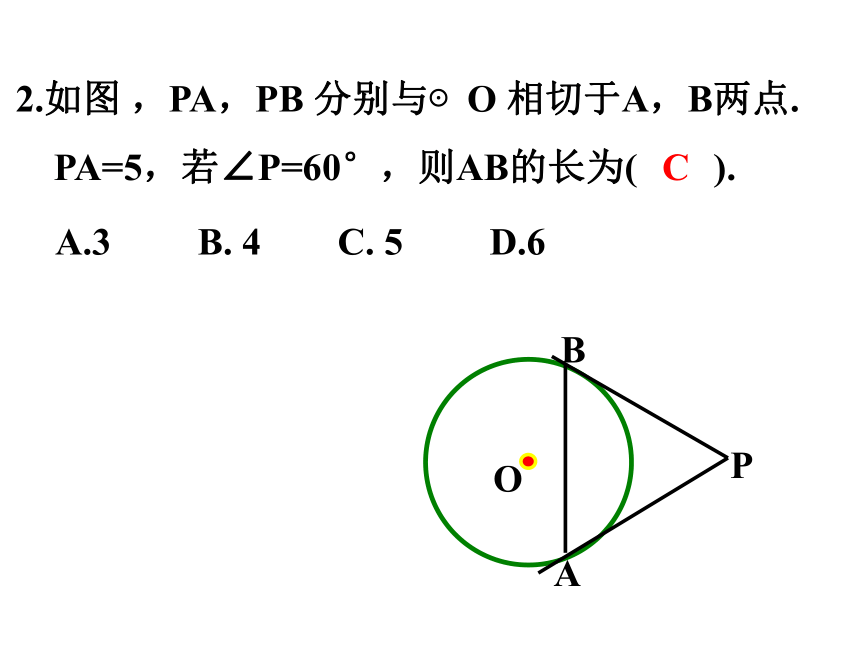
2.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
PA=5,若∠P=60°,则AB的长为( ).
O
A
B
P
A.3 B. 4 C. 5 D.6
C
3.如图,在△ABC中,AB=6,以点A为圆心,3
为半径的圆与边 BC 相切于点 D,与 AC,AB
分别交于点E和点 G,点F是优弧 CE 上一点,
∠CDE=18°,则∠ GFE的度数是 ( ) .
A.50° B.48° C.45° D.36°
A
B
C
G
F
D
E
B
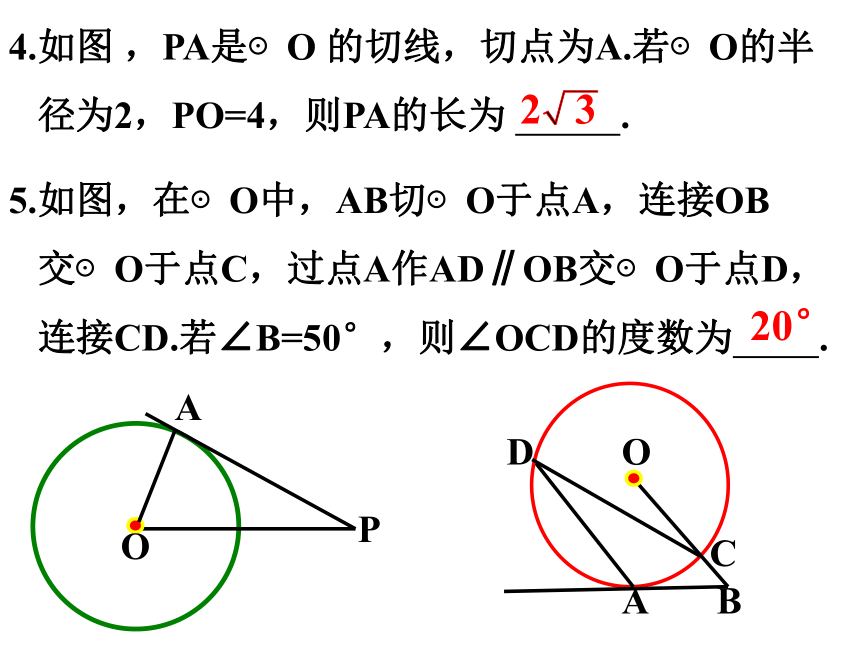
4.如图 ,PA是⊙O 的切线,切点为A.若⊙O的半
径为2,PO=4,则PA的长为 .
O
A
P
5.如图,在⊙O中,AB切⊙O于点A,连接OB
交⊙O于点C,过点A作AD∥OB交⊙O于点D,
连接CD.若∠B=50°,则∠OCD的度数为 .
O
B
A
C
D
20°
3
2
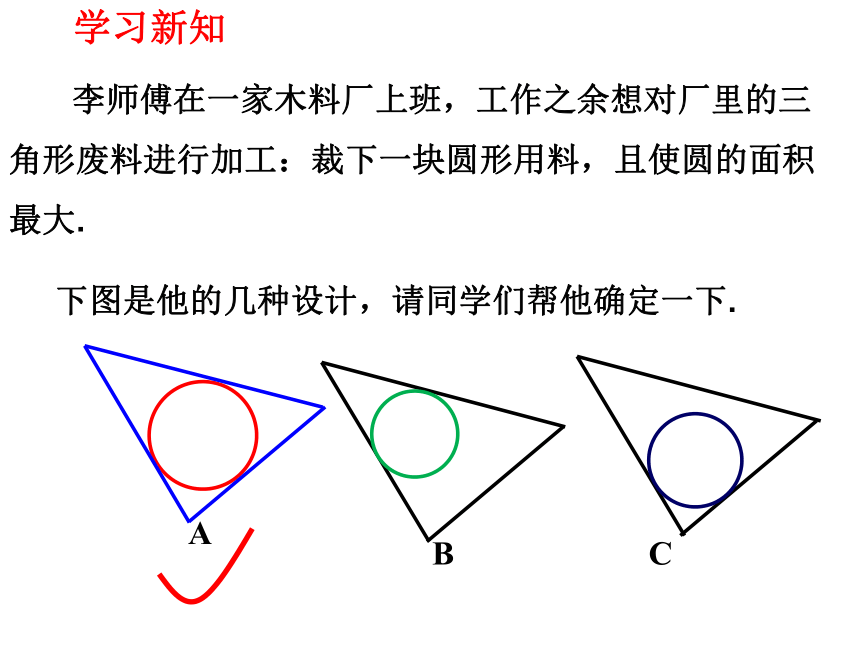
李师傅在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大.
下图是他的几种设计,请同学们帮他确定一下.
A
B
C
学习新知
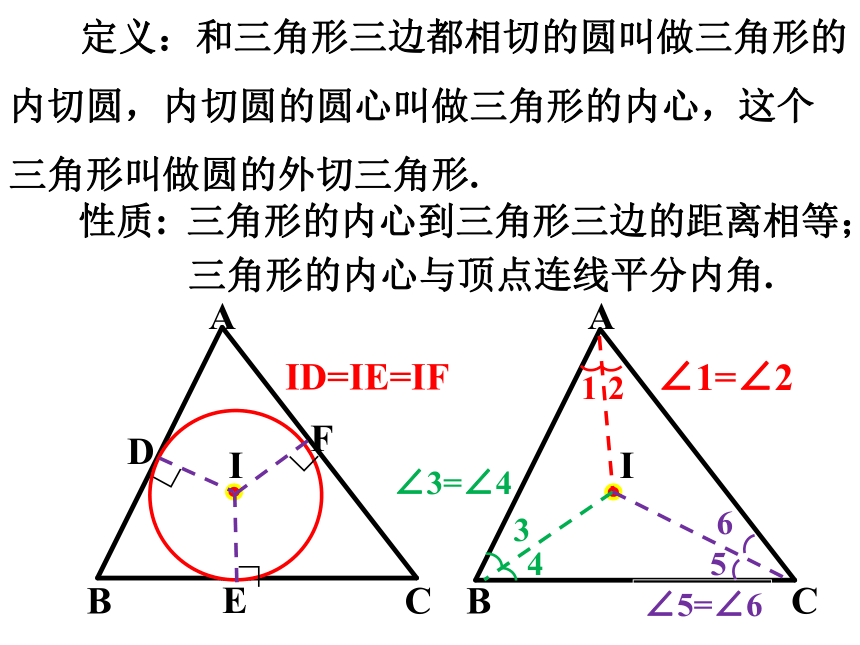
定义:和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
性质: 三角形的内心到三角形三边的距离相等;
A
B
C
三角形的内心与顶点连线平分内角.
D
E
F
I
∟
∟
∟
ID=IE=IF
A
B
C
I
1
2
3
4
5
6
∠1=∠2
∠3=∠4
∠5=∠6
A
B
C
作三角形内切圆的方法:
I
1.作∠ABC、∠ACB的平分线BM和CN,交点为I.
2.过点I作ID⊥BC,垂足为D.
3.以I为圆心,ID为半径作⊙I.
D
M
N
⊙I就是所求的圆.
解:∵点I是△ABC的内心,
∴ ∠BIC=180 °-(∠1+ ∠2)
= 180 °-(21.5°+ 30.5 °)
例 如图,在△ABC中,∠ABC=43°,∠ACB=61°,点I是内心, 求∠BIC的度数.
A
B
C
I
=128°
)
1
(
2
∴ ∠1= ∠ABC
= ×43°
1
2
1
2
= 21.5°,
∴ ∠2= ∠ACB
= ×61°
1
2
1
2
= 30.5°,
例题解析
解:设⊙A与BC相切于点D,
1. 在△ABC中,AB=AC=4cm,以点A为圆心,2cm为半径的圆与BC相切, 求∠BAC的度数.
A
B
C
D
连接AD,
则AD⊥BC.
∴ ∠BAC=2∠BAD.
在Rt△ABD中,
cos∠BAD=
AD
AB
∵ AB=AC,
=
2
4
=
1
2
∴ ∠BAD=60°.
∴ ∠BAC=120°.
练习巩固
解:∵点I是△ABC的内心,
∴ ∠BIC=180 °-(∠1+ ∠2)
= 180 °-( + )
2. 在△ABC中,∠A=80°,点I是内心, 求∠BIC的度数.
A
B
C
I
)
1
(
2
∴ ∠1= ∠ABC,
1
2
∠2= ∠ACB.
1
2
1
2
∠ABC
1
2
∠ACB
= 180 °- ( + )
1
2
∠ABC
∠ACB
= 180 °- ( 180°- )
1
2
∠A
= 90 °+
1
2
∠A
= 130 °.
O
B
A
C
r
解:
∵S△ABC=
S△ABO
+S△BCO
+S△ACO
∴S△ABC=
1
2
AB
r
+
1
2
BC
r
+
1
2
AC
r
=
1
2
r
(AB+BC+AC)
r
r
3. 在△ABC中,∠C=90°,BC=3,AC=4, 求这个三角形内切圆的半径.
∵ ∠C=90°,BC=3,AC=4,
∴ AB=5.
=
1
2
BC AC
∴
1
2
r(5+3+4)
=
1
2
×3 ×4,
∴ r=1.
设这个三角形内切圆的半径为r,
圆心为O,
连接OA,OB,OC.
O
B
A
C
D
F
解:
r
E
∴ r=CE=1.
设这个三角形内切圆的半径为r,
圆心为O,
切点分别为D,E,F.
∴AF=AD,
CE=CD.
BE=BF,
设AF=x,
CE=z.
BE=y,
∴
x+z=4
y+z=3
x+y=5
∴
x=3
y=2
z=1
∵∠C=90°,BC=3,AC=4,
∴ AB=5.
∵ ∠C=∠ODC=∠OEC,
∴ 四边形OECD是正方形.
OD=OE,
解:
∵ S△ABC=
1
2
AB
r
+
1
2
BC
r
+
1
2
AC
r
=
1
2
r
(AB+BC+AC)
∴
1
2
r 12
=6
∴ r=1.
如图,设这个三角形内切圆的半径为r,
4. 在一块周长为12cm,面积为6cm2的三角形材料中作一个内切圆,这个圆的半径是多少cm
A
B
C
r
O
r
(1)通过本节课的学习你学会了哪些知识?
(2)圆的切线和切线长相同吗?
(3)什么是三角形的内切圆和内心?
课堂小结
1.如图, ⊙O 是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为( ).
巩固提高
A.110° B. 120° C.1 30° D.140°
A
B
C
O
A
2.如图, ⊙O 是△ABC的内切圆,E,D,F分别是切点,若∠ABC=60°,∠ACB=80°,则∠EDF的度数为( ).
A.80° B. 70° C.60° D.50°
B
A
B
C
O
D
E
F
3.如图, 点O 是△ABC的心,∠A=90°,则∠BOC的度数为 .
A
B
C
O
135°
4.如图, △ABC的内切圆⊙O分别与边AB,BC,AC相切于点E,D,F,若BC=5,AE=7,则△ABC的周长为 .
24
A
B
C
O
D
E
F
5.在等腰△ABC中,点O是△ABC的内心,
OD⊥AB,若AB=AC=3,BC=2,OD= .
B
O
A
C
D
2
2
今天作业
课本P44页第2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.5三角形的内切圆 (1)
教学目标: 1.知道三角形内切圆、内心的概念,理解切线长定 理,并会用其解决有关问题; 2.经历探究切线长定理的过程,体会应用内切圆相 关知识解决问题,渗透转化思想.
教学重点: 切线长定理及其应用.
课件说明
复习旧知
过圆外一点作圆的两条切线,两条切线长
相等,圆心和这一点的连线平分两条切线的夹角.
切线长定理:
O
P
A
B
1.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
C是⊙O上一点,若∠P=50°,则∠ACB的
度数为( ).
O
A
B
P
C
A.50° B. 65° C. 100° D.130°
B
2.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
PA=5,若∠P=60°,则AB的长为( ).
O
A
B
P
A.3 B. 4 C. 5 D.6
C
3.如图,在△ABC中,AB=6,以点A为圆心,3
为半径的圆与边 BC 相切于点 D,与 AC,AB
分别交于点E和点 G,点F是优弧 CE 上一点,
∠CDE=18°,则∠ GFE的度数是 ( ) .
A.50° B.48° C.45° D.36°
A
B
C
G
F
D
E
B
4.如图 ,PA是⊙O 的切线,切点为A.若⊙O的半
径为2,PO=4,则PA的长为 .
O
A
P
5.如图,在⊙O中,AB切⊙O于点A,连接OB
交⊙O于点C,过点A作AD∥OB交⊙O于点D,
连接CD.若∠B=50°,则∠OCD的度数为 .
O
B
A
C
D
20°
3
2
李师傅在一家木料厂上班,工作之余想对厂里的三角形废料进行加工:裁下一块圆形用料,且使圆的面积最大.
下图是他的几种设计,请同学们帮他确定一下.
A
B
C
学习新知
定义:和三角形三边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.
性质: 三角形的内心到三角形三边的距离相等;
A
B
C
三角形的内心与顶点连线平分内角.
D
E
F
I
∟
∟
∟
ID=IE=IF
A
B
C
I
1
2
3
4
5
6
∠1=∠2
∠3=∠4
∠5=∠6
A
B
C
作三角形内切圆的方法:
I
1.作∠ABC、∠ACB的平分线BM和CN,交点为I.
2.过点I作ID⊥BC,垂足为D.
3.以I为圆心,ID为半径作⊙I.
D
M
N
⊙I就是所求的圆.
解:∵点I是△ABC的内心,
∴ ∠BIC=180 °-(∠1+ ∠2)
= 180 °-(21.5°+ 30.5 °)
例 如图,在△ABC中,∠ABC=43°,∠ACB=61°,点I是内心, 求∠BIC的度数.
A
B
C
I
=128°
)
1
(
2
∴ ∠1= ∠ABC
= ×43°
1
2
1
2
= 21.5°,
∴ ∠2= ∠ACB
= ×61°
1
2
1
2
= 30.5°,
例题解析
解:设⊙A与BC相切于点D,
1. 在△ABC中,AB=AC=4cm,以点A为圆心,2cm为半径的圆与BC相切, 求∠BAC的度数.
A
B
C
D
连接AD,
则AD⊥BC.
∴ ∠BAC=2∠BAD.
在Rt△ABD中,
cos∠BAD=
AD
AB
∵ AB=AC,
=
2
4
=
1
2
∴ ∠BAD=60°.
∴ ∠BAC=120°.
练习巩固
解:∵点I是△ABC的内心,
∴ ∠BIC=180 °-(∠1+ ∠2)
= 180 °-( + )
2. 在△ABC中,∠A=80°,点I是内心, 求∠BIC的度数.
A
B
C
I
)
1
(
2
∴ ∠1= ∠ABC,
1
2
∠2= ∠ACB.
1
2
1
2
∠ABC
1
2
∠ACB
= 180 °- ( + )
1
2
∠ABC
∠ACB
= 180 °- ( 180°- )
1
2
∠A
= 90 °+
1
2
∠A
= 130 °.
O
B
A
C
r
解:
∵S△ABC=
S△ABO
+S△BCO
+S△ACO
∴S△ABC=
1
2
AB
r
+
1
2
BC
r
+
1
2
AC
r
=
1
2
r
(AB+BC+AC)
r
r
3. 在△ABC中,∠C=90°,BC=3,AC=4, 求这个三角形内切圆的半径.
∵ ∠C=90°,BC=3,AC=4,
∴ AB=5.
=
1
2
BC AC
∴
1
2
r(5+3+4)
=
1
2
×3 ×4,
∴ r=1.
设这个三角形内切圆的半径为r,
圆心为O,
连接OA,OB,OC.
O
B
A
C
D
F
解:
r
E
∴ r=CE=1.
设这个三角形内切圆的半径为r,
圆心为O,
切点分别为D,E,F.
∴AF=AD,
CE=CD.
BE=BF,
设AF=x,
CE=z.
BE=y,
∴
x+z=4
y+z=3
x+y=5
∴
x=3
y=2
z=1
∵∠C=90°,BC=3,AC=4,
∴ AB=5.
∵ ∠C=∠ODC=∠OEC,
∴ 四边形OECD是正方形.
OD=OE,
解:
∵ S△ABC=
1
2
AB
r
+
1
2
BC
r
+
1
2
AC
r
=
1
2
r
(AB+BC+AC)
∴
1
2
r 12
=6
∴ r=1.
如图,设这个三角形内切圆的半径为r,
4. 在一块周长为12cm,面积为6cm2的三角形材料中作一个内切圆,这个圆的半径是多少cm
A
B
C
r
O
r
(1)通过本节课的学习你学会了哪些知识?
(2)圆的切线和切线长相同吗?
(3)什么是三角形的内切圆和内心?
课堂小结
1.如图, ⊙O 是△ABC的内切圆,且∠ABC=60°,∠ACB=80°,则∠BOC的度数为( ).
巩固提高
A.110° B. 120° C.1 30° D.140°
A
B
C
O
A
2.如图, ⊙O 是△ABC的内切圆,E,D,F分别是切点,若∠ABC=60°,∠ACB=80°,则∠EDF的度数为( ).
A.80° B. 70° C.60° D.50°
B
A
B
C
O
D
E
F
3.如图, 点O 是△ABC的心,∠A=90°,则∠BOC的度数为 .
A
B
C
O
135°
4.如图, △ABC的内切圆⊙O分别与边AB,BC,AC相切于点E,D,F,若BC=5,AE=7,则△ABC的周长为 .
24
A
B
C
O
D
E
F
5.在等腰△ABC中,点O是△ABC的内心,
OD⊥AB,若AB=AC=3,BC=2,OD= .
B
O
A
C
D
2
2
今天作业
课本P44页第2、3题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
