24.4 直线与圆的位置关系(3)课件 (共25张PPT)
文档属性
| 名称 | 24.4 直线与圆的位置关系(3)课件 (共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 19:28:55 | ||
图片预览



文档简介
(共25张PPT)
沪科版 九年级下册
24.4直线和圆的位置关系(3)
教学目标: 1.理解切线长定理,并会用其解决有关问题; 2.经历探究切线长定理的过程,体会应用内切圆相 关知识解决问题,渗透转化思想.
教学重点: 切线长定理及其应用.
课件说明
圆的切线垂直于过切点的半径.
切线的性质
经过半径的外端并且垂直于
这条半径的直线是圆的切线.
切线的判定
复习旧知
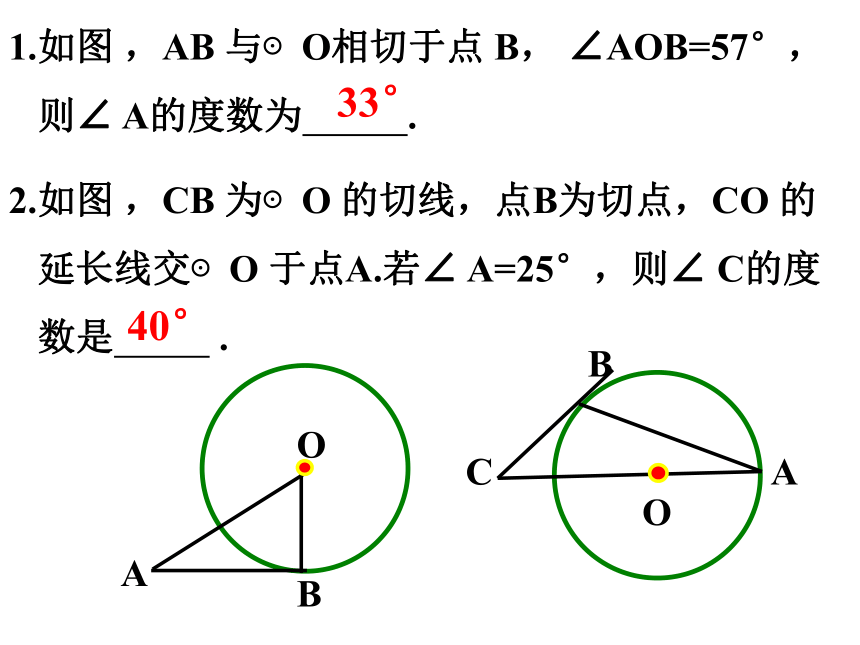
2.如图 ,CB 为⊙O 的切线,点B为切点,CO 的
延长线交⊙O 于点A.若∠ A=25°,则∠ C的度
数是 .
1.如图 ,AB 与⊙O相切于点 B, ∠AOB=57°,
则∠ A的度数为 .
O
A
B
33°
O
A
B
C
40°
O
P
A
B
∟
∟
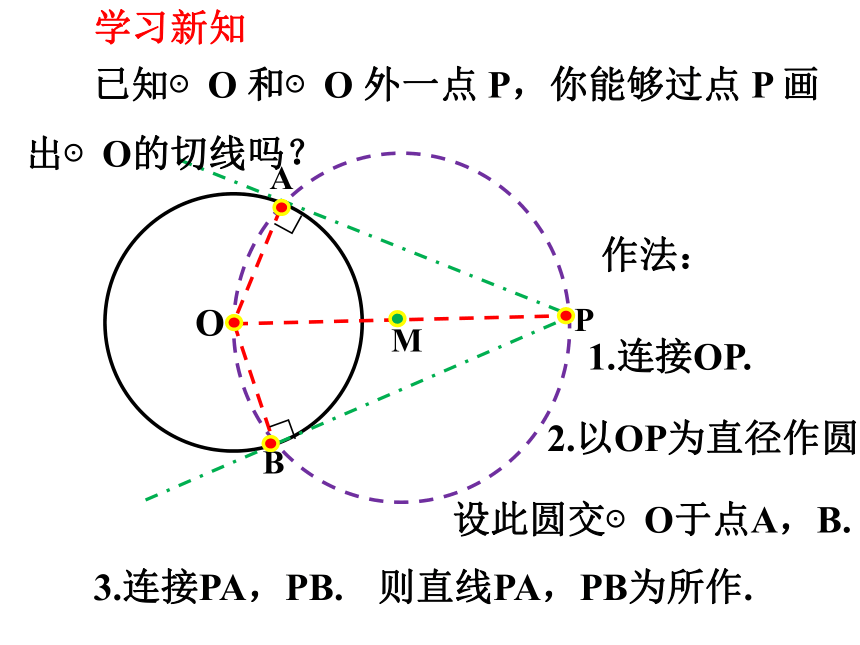
已知⊙O 和⊙O 外一点 P,你能够过点 P 画出⊙O的切线吗?
M
作法:
1.连接OP.
2.以OP为直径作圆,
设此圆交⊙O于点A,B.
3.连接PA,PB.
则直线PA,PB为所作.
学习新知
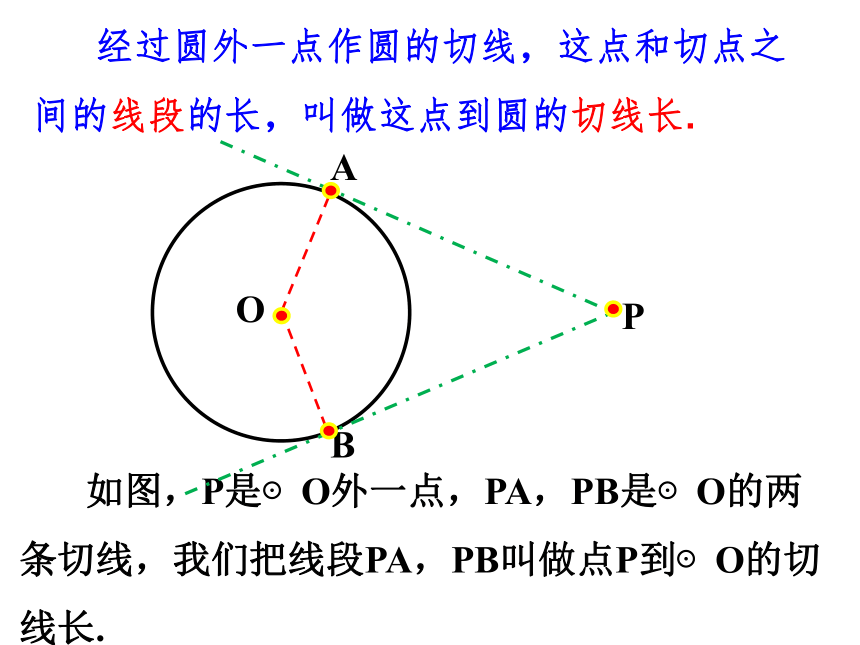
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长.
O
P
A
B
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
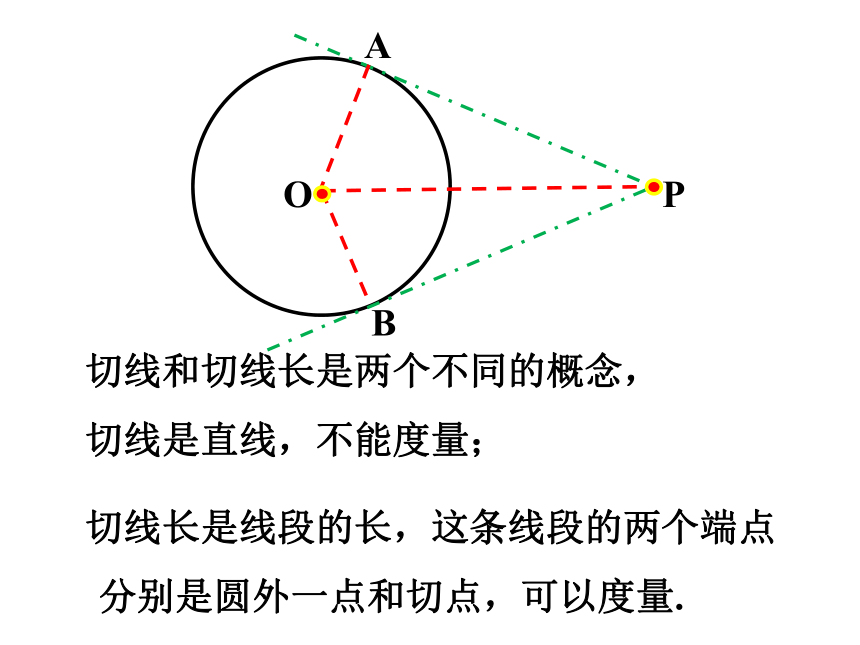
切线和切线长是两个不同的概念,
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
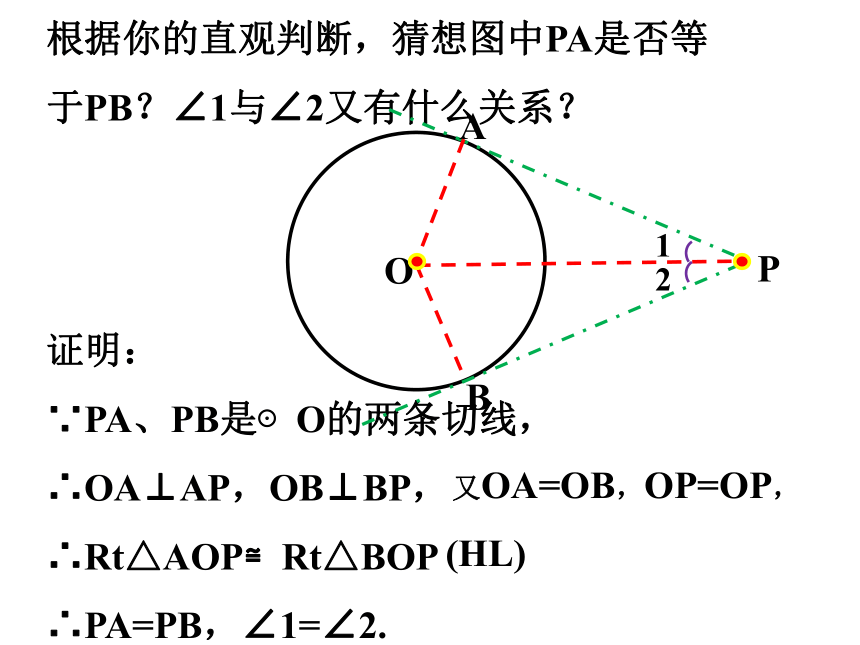
根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
证明:
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴Rt△AOP≌Rt△BOP
∴PA=PB,∠1=∠2.
又OA=OB,OP=OP,
(HL)
O
P
A
B
1
2
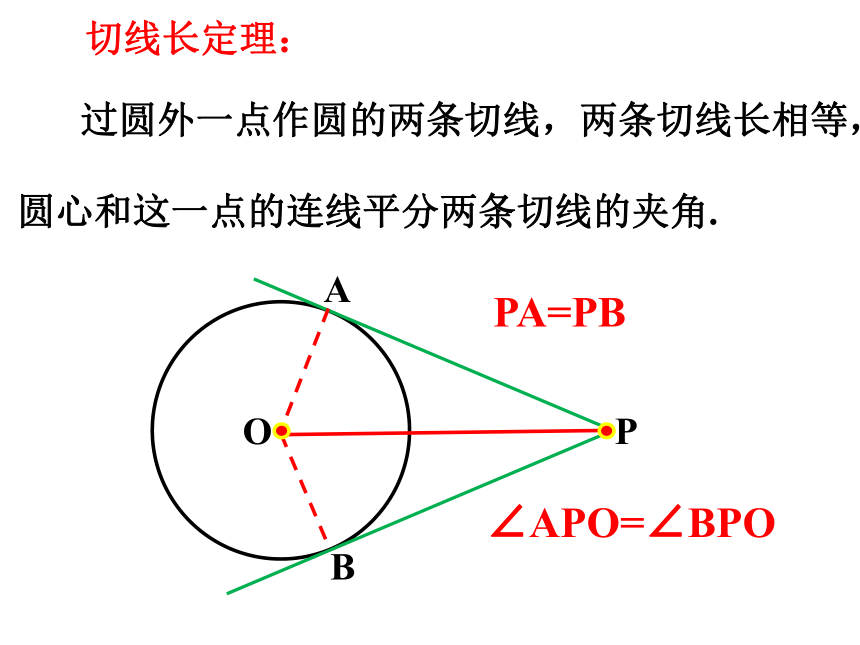
过圆外一点作圆的两条切线,两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
切线长定理:
O
P
A
B
PA=PB
∠APO=∠BPO
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(1)写出图中所有的垂直关系;
OA⊥PA,
基本图形的探究
B
A
P
O
C
Q
D
OB ⊥PB,
AB ⊥OP;
(2)写出图中所有的全等三角形;
△AOP≌△BOP,
△AOC≌△BOC,
△ACP≌ △BCP;
练习巩固
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(3)写出图中与∠OAC相等的角
∠OAC=
基本图形的探究
B
A
P
O
C
Q
D
∠OBC
=∠APC
=∠BPC
(4)写出图中所有的等腰三角形
△ABP,
△AOB
练习巩固
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(5)图中除半径外,还有那些相等的线段?
AC=BC
基本图形的探究
B
A
P
O
C
Q
D
PA=PB
(6)图中有哪些相等的弧?
AD
BD
=
AQ
BQ
=
练习巩固
A
O
H
G
F
D
E
C
B
.
例5.已知:如图,四边形ABCD的边AB,
BC,CD,DA和分别相切于点E,F,G,H.
求证:AB+CD=DA+BC.
证明:
∵AE、AH是⊙O的两条切线,
∴AE=AH,
同理
BE=BF,
CG=CF,
DG=DH.
∴ AE+BE+CG+DG=
AH+BF+CF+DH
∴ AB+CD=DA+BC.
例题解析
A
O
H
G
F
D
E
C
B
.
例5.已知:如图,四边形ABCD的边AB,BC,CD,DA和分别相切于点E,F,G,H.
求证:AB+CD=DA+BC.
各边都和圆相切.
这个四边形ABCD有什么特点?
各边都和圆相切的四边形又有什么特性
各边都和圆相切的四边形的对边和相等.
1.已知:⊙O的半径是30cm,点P与圆心O的距离是60cm,PA、PB是⊙O的两条切线,A、B是切点, 求∠APB的大小与PA的长.
B
A
P
O
解:
∵PA、PB是⊙O的两条切线,
∴∠APB=
2∠APO,
OA⊥PA.
在Rt△AOP中,
∴sin∠APO=
OA=30cm,
OP=60cm,
OA
OP
如图,
=
30
60
=
1
2
∴∠APO=30°,
∴∠APB=60°.
1.已知:⊙O的半径是30cm,点P与圆心O的距离是60cm,PA、PB是⊙O的两条切线,A、B是切点, 求∠APB的大小与PA的长.
B
A
P
O
在Rt△AOP中,
cos∠APO=
PA
OP
∴PA=
=60cos30°
OPcos∠APO
=60×
2
3
3 (cm).
=30
2.已知:PA、PB是⊙O的两条切线,A、B是切点, ∠APB=60°,点C是⊙O上异于点A、B的任意一点,求∠ACB的大小.
B
A
P
O
解:
当点C是⊙O的优弧上时,
C
连接AC,BC.
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴ OAP=∠OPB= 90°.
∵ ∠APB=60°,
∴ AOB=120°.
∴ ACB=60°.
2.已知:PA、PB是⊙O的两条切线,A、B是切点, ∠APB=60°,点C是⊙O上异于点A、B的任意一点,求∠ACB的大小.
B
A
P
O
解:
当点C是⊙O的劣弧上时,
C
连接AC,BC,AB.
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴ OAP=∠OPB= 90°.
∵ ∠APB=60°,
∴ AOB=120°.
∴ ACB=120°.
∴ BAC+ ABC=60°,
(1)通过本节课的学习你学会了哪些知识?
(2)圆的切线和切线长相同吗?
课堂小结
1.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
若PA=5,则PB= .
巩固提高
2.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
若∠OAB=38°,则∠P的度数为 .
O
A
B
P
O
A
B
P
5
76°
3.如图 ,PA,PB ,DC是⊙O 的切线,A,B,C
为切点.若PD=8,PB=5,则DC= .
C
O
A
B
P
D
3
4.如图 ,PA,PB 是⊙O 的切线, ∠P=102°,
则∠A+∠C的度数为 .
O
A
B
P
D
C
219°
5.如图 ,四边形ABCD是边长为10cm的正方形,
以AB为直径作⊙O ,从顶点D作⊙O的切线
DE,延长DE交BC于点F,则△ DCF的面积
为 cm2.
O
A
B
C
F
D
E
37.5
DF2=FC2+DC2
x
(10+x)2=(10-x)2+102
x=2.5
FC=7.5
今天作业
课本P40页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.4直线和圆的位置关系(3)
教学目标: 1.理解切线长定理,并会用其解决有关问题; 2.经历探究切线长定理的过程,体会应用内切圆相 关知识解决问题,渗透转化思想.
教学重点: 切线长定理及其应用.
课件说明
圆的切线垂直于过切点的半径.
切线的性质
经过半径的外端并且垂直于
这条半径的直线是圆的切线.
切线的判定
复习旧知
2.如图 ,CB 为⊙O 的切线,点B为切点,CO 的
延长线交⊙O 于点A.若∠ A=25°,则∠ C的度
数是 .
1.如图 ,AB 与⊙O相切于点 B, ∠AOB=57°,
则∠ A的度数为 .
O
A
B
33°
O
A
B
C
40°
O
P
A
B
∟
∟
已知⊙O 和⊙O 外一点 P,你能够过点 P 画出⊙O的切线吗?
M
作法:
1.连接OP.
2.以OP为直径作圆,
设此圆交⊙O于点A,B.
3.连接PA,PB.
则直线PA,PB为所作.
学习新知
如图,P是⊙O外一点,PA,PB是⊙O的两条切线,我们把线段PA,PB叫做点P到⊙O的切线长.
O
P
A
B
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
切线和切线长是两个不同的概念,
切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
O
P
A
B
根据你的直观判断,猜想图中PA是否等于PB?∠1与∠2又有什么关系?
证明:
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴Rt△AOP≌Rt△BOP
∴PA=PB,∠1=∠2.
又OA=OB,OP=OP,
(HL)
O
P
A
B
1
2
过圆外一点作圆的两条切线,两条切线长相等,圆心和这一点的连线平分两条切线的夹角.
切线长定理:
O
P
A
B
PA=PB
∠APO=∠BPO
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(1)写出图中所有的垂直关系;
OA⊥PA,
基本图形的探究
B
A
P
O
C
Q
D
OB ⊥PB,
AB ⊥OP;
(2)写出图中所有的全等三角形;
△AOP≌△BOP,
△AOC≌△BOC,
△ACP≌ △BCP;
练习巩固
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(3)写出图中与∠OAC相等的角
∠OAC=
基本图形的探究
B
A
P
O
C
Q
D
∠OBC
=∠APC
=∠BPC
(4)写出图中所有的等腰三角形
△ABP,
△AOB
练习巩固
1.如图,PA、PB是⊙O的两条切线,A、B为切点,直线OP交⊙O于点D、E,交AB于C.
(5)图中除半径外,还有那些相等的线段?
AC=BC
基本图形的探究
B
A
P
O
C
Q
D
PA=PB
(6)图中有哪些相等的弧?
AD
BD
=
AQ
BQ
=
练习巩固
A
O
H
G
F
D
E
C
B
.
例5.已知:如图,四边形ABCD的边AB,
BC,CD,DA和分别相切于点E,F,G,H.
求证:AB+CD=DA+BC.
证明:
∵AE、AH是⊙O的两条切线,
∴AE=AH,
同理
BE=BF,
CG=CF,
DG=DH.
∴ AE+BE+CG+DG=
AH+BF+CF+DH
∴ AB+CD=DA+BC.
例题解析
A
O
H
G
F
D
E
C
B
.
例5.已知:如图,四边形ABCD的边AB,BC,CD,DA和分别相切于点E,F,G,H.
求证:AB+CD=DA+BC.
各边都和圆相切.
这个四边形ABCD有什么特点?
各边都和圆相切的四边形又有什么特性
各边都和圆相切的四边形的对边和相等.
1.已知:⊙O的半径是30cm,点P与圆心O的距离是60cm,PA、PB是⊙O的两条切线,A、B是切点, 求∠APB的大小与PA的长.
B
A
P
O
解:
∵PA、PB是⊙O的两条切线,
∴∠APB=
2∠APO,
OA⊥PA.
在Rt△AOP中,
∴sin∠APO=
OA=30cm,
OP=60cm,
OA
OP
如图,
=
30
60
=
1
2
∴∠APO=30°,
∴∠APB=60°.
1.已知:⊙O的半径是30cm,点P与圆心O的距离是60cm,PA、PB是⊙O的两条切线,A、B是切点, 求∠APB的大小与PA的长.
B
A
P
O
在Rt△AOP中,
cos∠APO=
PA
OP
∴PA=
=60cos30°
OPcos∠APO
=60×
2
3
3 (cm).
=30
2.已知:PA、PB是⊙O的两条切线,A、B是切点, ∠APB=60°,点C是⊙O上异于点A、B的任意一点,求∠ACB的大小.
B
A
P
O
解:
当点C是⊙O的优弧上时,
C
连接AC,BC.
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴ OAP=∠OPB= 90°.
∵ ∠APB=60°,
∴ AOB=120°.
∴ ACB=60°.
2.已知:PA、PB是⊙O的两条切线,A、B是切点, ∠APB=60°,点C是⊙O上异于点A、B的任意一点,求∠ACB的大小.
B
A
P
O
解:
当点C是⊙O的劣弧上时,
C
连接AC,BC,AB.
∵PA、PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP,
∴ OAP=∠OPB= 90°.
∵ ∠APB=60°,
∴ AOB=120°.
∴ ACB=120°.
∴ BAC+ ABC=60°,
(1)通过本节课的学习你学会了哪些知识?
(2)圆的切线和切线长相同吗?
课堂小结
1.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
若PA=5,则PB= .
巩固提高
2.如图 ,PA,PB 分别与⊙O 相切于A,B两点.
若∠OAB=38°,则∠P的度数为 .
O
A
B
P
O
A
B
P
5
76°
3.如图 ,PA,PB ,DC是⊙O 的切线,A,B,C
为切点.若PD=8,PB=5,则DC= .
C
O
A
B
P
D
3
4.如图 ,PA,PB 是⊙O 的切线, ∠P=102°,
则∠A+∠C的度数为 .
O
A
B
P
D
C
219°
5.如图 ,四边形ABCD是边长为10cm的正方形,
以AB为直径作⊙O ,从顶点D作⊙O的切线
DE,延长DE交BC于点F,则△ DCF的面积
为 cm2.
O
A
B
C
F
D
E
37.5
DF2=FC2+DC2
x
(10+x)2=(10-x)2+102
x=2.5
FC=7.5
今天作业
课本P40页第8、9题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
