24.6 正多边形与圆(2)课件 (共25张PPT)
文档属性
| 名称 | 24.6 正多边形与圆(2)课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 966.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
沪科版 九年级下册
24.6正多边形与圆(2)
教学目标:
1.理解正多边形和圆的关系,知道把圆分成相等的
一些弧,就可以得到这个圆的内接正多边形;
2.理解正多边形的边长、半径、边心距和中心角等
概念,会计算正多边形的边长、半径、边心距、
中心角、周长和面积.
教学重点:
正多边形的有关计算问题.
课件说明
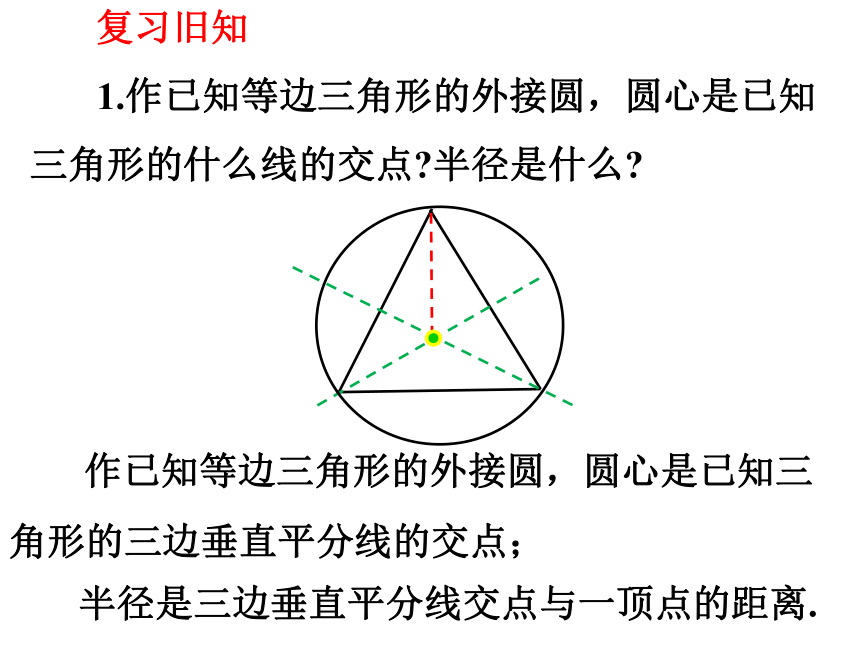
1.作已知等边三角形的外接圆,圆心是已知三角形的什么线的交点 半径是什么
作已知等边三角形的外接圆,圆心是已知三角形的三边垂直平分线的交点;
半径是三边垂直平分线交点与一顶点的距离.
复习旧知
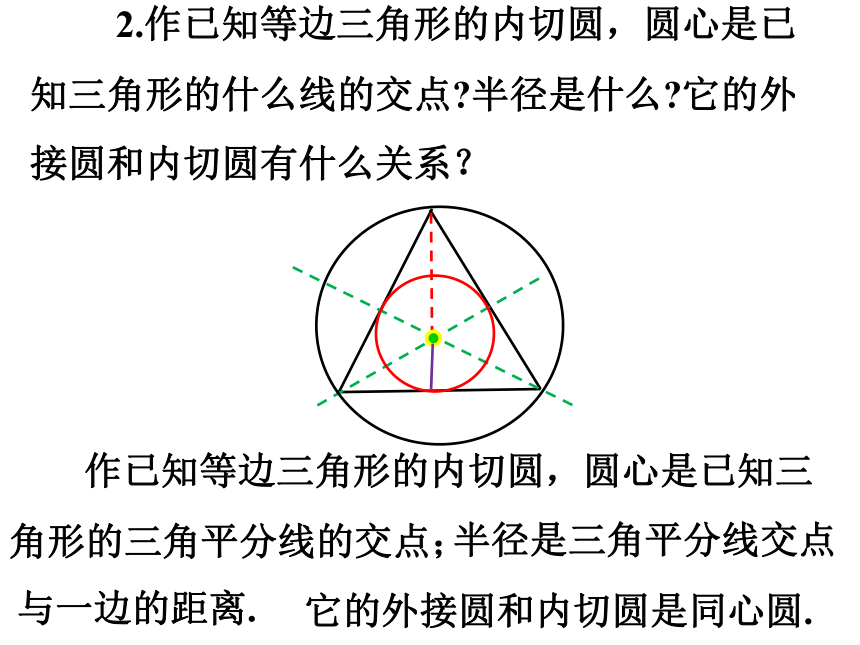
作已知等边三角形的内切圆,圆心是已知三角形的三角平分线的交点;
2.作已知等边三角形的内切圆,圆心是已知三角形的什么线的交点 半径是什么 它的外接圆和内切圆有什么关系?
它的外接圆和内切圆是同心圆.
半径是三角平分线交点
与一边的距离.
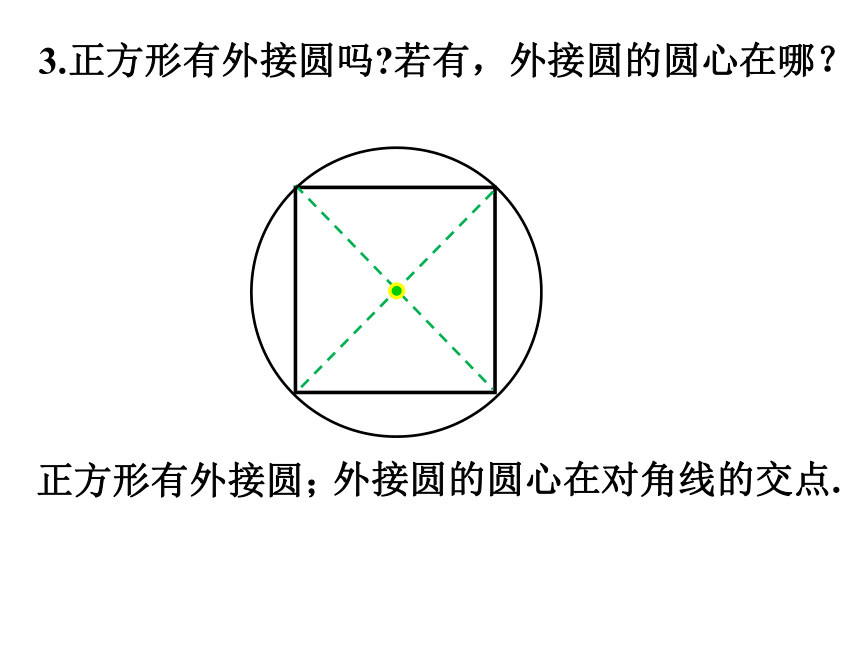
3.正方形有外接圆吗 若有,外接圆的圆心在哪?
正方形有外接圆;
外接圆的圆心在对角线的交点.
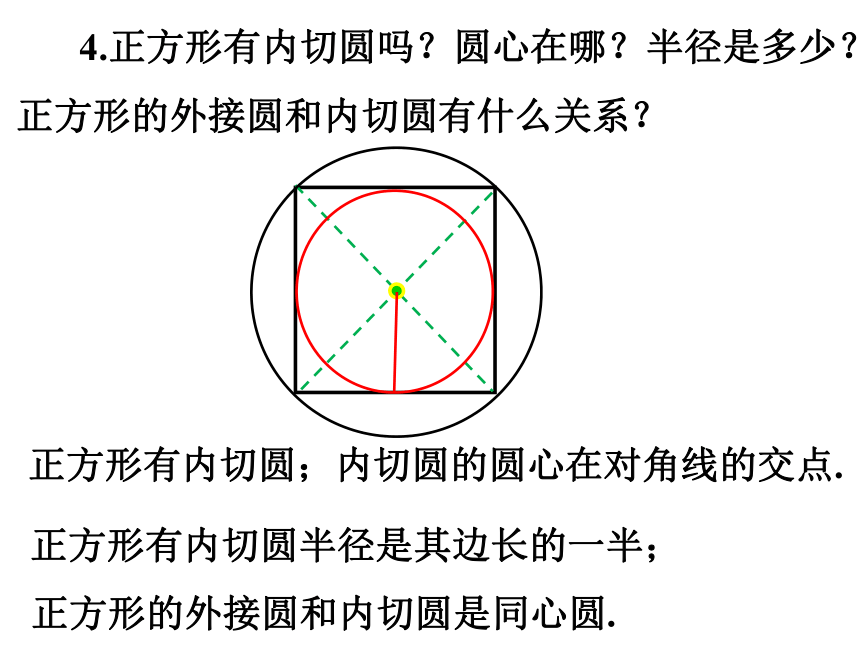
4.正方形有内切圆吗?圆心在哪?半径是多少?正方形的外接圆和内切圆有什么关系?
正方形有内切圆;内切圆的圆心在对角线的交点.
正方形有内切圆半径是其边长的一半;
正方形的外接圆和内切圆是同心圆.
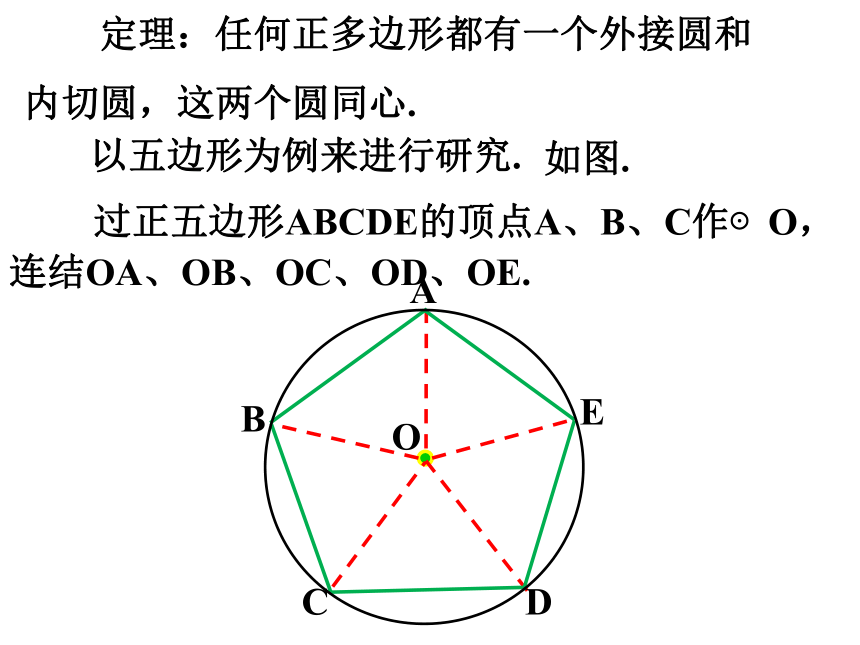
定理:任何正多边形都有一个外接圆和内切圆,这两个圆同心.
以五边形为例来进行研究.
过正五边形ABCDE的顶点A、B、C作⊙O,
连结OA、OB、OC、OD、OE.
如图.
A
B
C
D
E
O
A
B
C
D
E
O
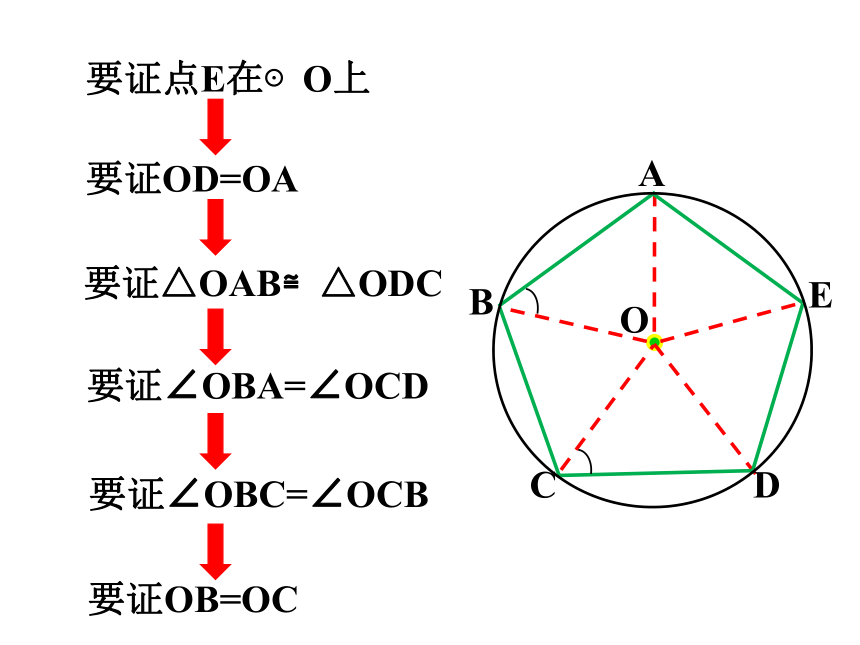
要证OD=OA
要证点E在⊙O上
要证△OAB≌△ODC
要证∠OBA=∠OCD
要证∠OBC=∠OCB
要证OB=OC
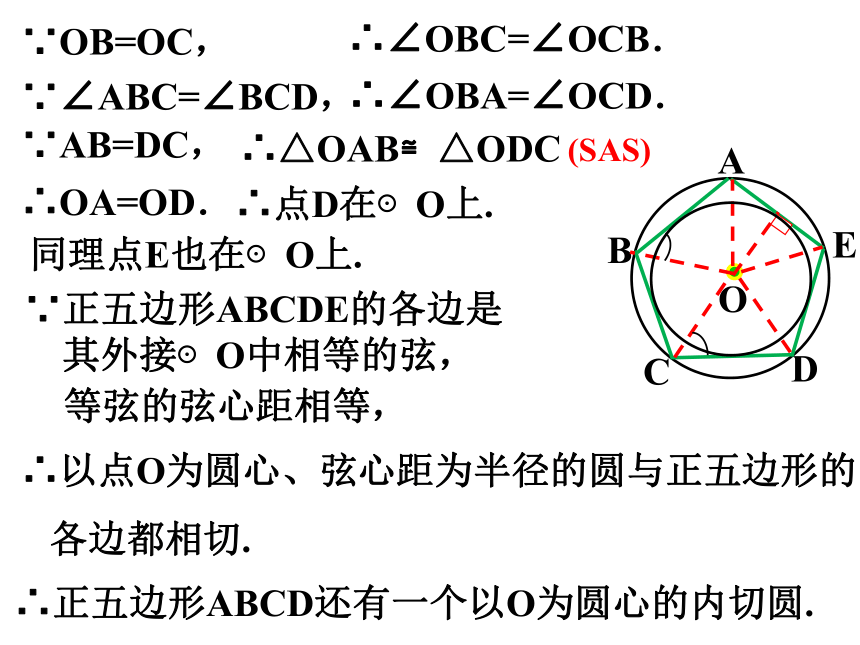
∵OB=OC,
∴∠OBC=∠OCB.
∵∠ABC=∠BCD,
∴∠OBA=∠OCD.
∵AB=DC,
∴△OAB≌△ODC
∴OA=OD.
∴点D在⊙O上.
同理点E也在⊙O上.
∵正五边形ABCDE的各边是
其外接⊙O中相等的弦,
∴以点O为圆心、弦心距为半径的圆与正五边形的
各边都相切.
∴正五边形ABCD还有一个以O为圆心的内切圆.
O
A
B
C
D
E
等弦的弦心距相等,
(SAS)
定理:任何正多边形都有一个外接圆和内切圆,这两个圆同心.
A
B
C
D
E
O
学习新知
A
B
C
E
D
F
与正多边形的有关概念.
O
(
3.正多边形的半径
半径R
1.正多边形的中心
2.正多边形的中心角
4.正多边形的边心距
中心角
边心距r
一个正多边形的外接圆和内切圆的公共圆心.
外接圆的半径
内切圆的半径.
正多边形的每一条边所对的圆心角.
学习新知
E
F
C
D
.
O
A
B
G
边心距把△AOB分成2个全等的直角三角形.
R
a
边心距
学习新知
正 n 边形的中心角度数如何计算?
正 n 边形的一个外角度数如何计算?
中心角的度数=
一个外角的度数=
O
A
B
C
D
E
(
学习新知
E
F
C
D
.
O
A
B
G
设正多边形的边长为a,半径为R,
R
a
边心距
正 n 边形的周长如何计算?
正 n 边形的周长为
L=na.
边心距为d.
正 n 边形的面积如何计算?
正 n 边形的面积为
S=
正 n 边形的边心距如何计算?
正 n 边形的边心距为
d= R2- ( a)2.
1
2
1
2
ad
n
=
1
2
Ld
1.O是正△ABC的中心,它是△ABC的______圆与______圆的圆心.
2.OB是正△ABC的______圆的_____.
3.OD叫作正△ABC的________,
它是正△ABC的______圆的半径.
A
B
C
O
D
外接
内切
半径
外接
边心距
内切
练习巩固
4.正n边形的一个内角的度数是__________;
一个外角的度数是_____;中心角的度数是____;正多边形的中心角与外角的大小关系是_______.
相等
360°
n
360°
n
(n-2) ·180°
n
正多边形都是轴对称图形,一个正n边形共有_条对称轴,每条对称轴都通过正n边形的____.
n
中心
探究新知
边数是偶数的正多边形还是中心对称
图形,它的中心就是对称中心.
例.求边长为a的正六边形的周长和面积.
F
A
D
E
.
O
B
C
G
解:
过正六边形中心O作OG⊥BC,垂足是G.
∵多边形ABCDEF正六边形,
∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OG=
=
a
2
3
∴OB=OC=BC=a.
OB2- ( BC)2
1
2
= a2- ( a)2
1
2
∴正六边形的周长 L=6 a=6a.
∴正六边形的面积 S=
6
1
2
BC
OG
=6
1
2
a
a
2
3
=
a2
2
3
3
2.若一个正多边形的一个外角等于18°,则
这个正多边形的边数是 .
1.正九边形的一个内角的度数是( ).
A.108° B. 120° C. 135° D.140°
练习巩固
20
D
3.如果一个正多边形的中心角等于72°,
那么这个正多边形的边数为 .
5
4.正六边形的边长为 1,则它的半径为___,
面积为______.
F
A
B
D
C
E
O
P
1
1
3
3
5.如图,在正六边形ABCDEF中,AC= ,
那么它的边长是( ).
A. 1 B. C. D. 2
A
B
C
D
E
F
3
2
3
2
D
今天作业
课本P52页第4、6、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.6正多边形与圆(2)
教学目标:
1.理解正多边形和圆的关系,知道把圆分成相等的
一些弧,就可以得到这个圆的内接正多边形;
2.理解正多边形的边长、半径、边心距和中心角等
概念,会计算正多边形的边长、半径、边心距、
中心角、周长和面积.
教学重点:
正多边形的有关计算问题.
课件说明
1.作已知等边三角形的外接圆,圆心是已知三角形的什么线的交点 半径是什么
作已知等边三角形的外接圆,圆心是已知三角形的三边垂直平分线的交点;
半径是三边垂直平分线交点与一顶点的距离.
复习旧知
作已知等边三角形的内切圆,圆心是已知三角形的三角平分线的交点;
2.作已知等边三角形的内切圆,圆心是已知三角形的什么线的交点 半径是什么 它的外接圆和内切圆有什么关系?
它的外接圆和内切圆是同心圆.
半径是三角平分线交点
与一边的距离.
3.正方形有外接圆吗 若有,外接圆的圆心在哪?
正方形有外接圆;
外接圆的圆心在对角线的交点.
4.正方形有内切圆吗?圆心在哪?半径是多少?正方形的外接圆和内切圆有什么关系?
正方形有内切圆;内切圆的圆心在对角线的交点.
正方形有内切圆半径是其边长的一半;
正方形的外接圆和内切圆是同心圆.
定理:任何正多边形都有一个外接圆和内切圆,这两个圆同心.
以五边形为例来进行研究.
过正五边形ABCDE的顶点A、B、C作⊙O,
连结OA、OB、OC、OD、OE.
如图.
A
B
C
D
E
O
A
B
C
D
E
O
要证OD=OA
要证点E在⊙O上
要证△OAB≌△ODC
要证∠OBA=∠OCD
要证∠OBC=∠OCB
要证OB=OC
∵OB=OC,
∴∠OBC=∠OCB.
∵∠ABC=∠BCD,
∴∠OBA=∠OCD.
∵AB=DC,
∴△OAB≌△ODC
∴OA=OD.
∴点D在⊙O上.
同理点E也在⊙O上.
∵正五边形ABCDE的各边是
其外接⊙O中相等的弦,
∴以点O为圆心、弦心距为半径的圆与正五边形的
各边都相切.
∴正五边形ABCD还有一个以O为圆心的内切圆.
O
A
B
C
D
E
等弦的弦心距相等,
(SAS)
定理:任何正多边形都有一个外接圆和内切圆,这两个圆同心.
A
B
C
D
E
O
学习新知
A
B
C
E
D
F
与正多边形的有关概念.
O
(
3.正多边形的半径
半径R
1.正多边形的中心
2.正多边形的中心角
4.正多边形的边心距
中心角
边心距r
一个正多边形的外接圆和内切圆的公共圆心.
外接圆的半径
内切圆的半径.
正多边形的每一条边所对的圆心角.
学习新知
E
F
C
D
.
O
A
B
G
边心距把△AOB分成2个全等的直角三角形.
R
a
边心距
学习新知
正 n 边形的中心角度数如何计算?
正 n 边形的一个外角度数如何计算?
中心角的度数=
一个外角的度数=
O
A
B
C
D
E
(
学习新知
E
F
C
D
.
O
A
B
G
设正多边形的边长为a,半径为R,
R
a
边心距
正 n 边形的周长如何计算?
正 n 边形的周长为
L=na.
边心距为d.
正 n 边形的面积如何计算?
正 n 边形的面积为
S=
正 n 边形的边心距如何计算?
正 n 边形的边心距为
d= R2- ( a)2.
1
2
1
2
ad
n
=
1
2
Ld
1.O是正△ABC的中心,它是△ABC的______圆与______圆的圆心.
2.OB是正△ABC的______圆的_____.
3.OD叫作正△ABC的________,
它是正△ABC的______圆的半径.
A
B
C
O
D
外接
内切
半径
外接
边心距
内切
练习巩固
4.正n边形的一个内角的度数是__________;
一个外角的度数是_____;中心角的度数是____;正多边形的中心角与外角的大小关系是_______.
相等
360°
n
360°
n
(n-2) ·180°
n
正多边形都是轴对称图形,一个正n边形共有_条对称轴,每条对称轴都通过正n边形的____.
n
中心
探究新知
边数是偶数的正多边形还是中心对称
图形,它的中心就是对称中心.
例.求边长为a的正六边形的周长和面积.
F
A
D
E
.
O
B
C
G
解:
过正六边形中心O作OG⊥BC,垂足是G.
∵多边形ABCDEF正六边形,
∴∠BOC=60°.
∵OB=OC,
∴△OBC是等边三角形,
∴OG=
=
a
2
3
∴OB=OC=BC=a.
OB2- ( BC)2
1
2
= a2- ( a)2
1
2
∴正六边形的周长 L=6 a=6a.
∴正六边形的面积 S=
6
1
2
BC
OG
=6
1
2
a
a
2
3
=
a2
2
3
3
2.若一个正多边形的一个外角等于18°,则
这个正多边形的边数是 .
1.正九边形的一个内角的度数是( ).
A.108° B. 120° C. 135° D.140°
练习巩固
20
D
3.如果一个正多边形的中心角等于72°,
那么这个正多边形的边数为 .
5
4.正六边形的边长为 1,则它的半径为___,
面积为______.
F
A
B
D
C
E
O
P
1
1
3
3
5.如图,在正六边形ABCDEF中,AC= ,
那么它的边长是( ).
A. 1 B. C. D. 2
A
B
C
D
E
F
3
2
3
2
D
今天作业
课本P52页第4、6、8题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
