24.7 弧长与扇形面积(1)课件 (共25张PPT)
文档属性
| 名称 | 24.7 弧长与扇形面积(1)课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
沪科版 九年级下册
24.7弧长和扇形面积(1)
教学目标:
理解 1°的圆心角所对的弧长等于圆周长的 ,
所对的扇形面积等于圆面积的 ;能够发现 n°
的圆心角所对的弧长和扇形面积都是 1°的圆心角
所对的弧长和扇形面积的 n 倍;能利用弧长表示扇
形面积.并能利用公式计算弧长和扇形面积.
课件说明
教学重点:
弧长和扇形面积公式的推导及运用.
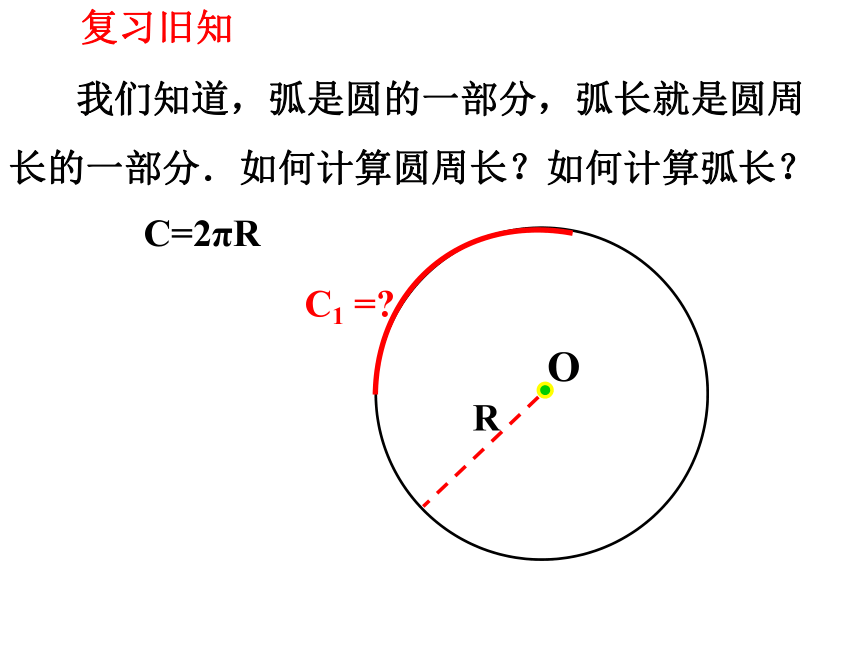
我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
O
C=2πR
R
C1 =
复习旧知
(1)圆的周长可以看作是多少度的圆心角所对的弧长?
360°.
(2)在同圆或等圆中,每一个 1°的圆心角所对的
弧长有怎样的关系?
相等.
(3) 1°的圆心角所对的弧长是多少?
圆周长的 .
(4) n°的圆心角所对的弧长是多少?
是1°的圆心角所对弧长的 n 倍.
1
360
(5)怎样计算半径为 R 的圆中,1°的圆心角所对 的弧长?
1°的圆心角所对弧长是圆周长的 ,
为
.
(6)怎样计算半径为 R 的圆中,2°的圆心角所对 的弧长?
2°是 1°的 2 倍,所以弧长也是 1°的圆心角所对
弧长的 2 倍,为 .
2πR
360
=
πR
180
1
360
(7)怎样计算半径为 R 的圆中,5°的圆心角所对 的弧长?
5°是 1°的 5 倍,所以弧长也是 1°的圆心角所对
弧长的 5 倍,为 .
(8)怎样计算半径为 R 的圆中,n°的圆心角所对 的弧长?
n°是 1°的 n 倍,所以弧长也是 1°的圆心角所对
弧长的 n 倍,为 .
nπR
180
弧长的大小由哪些量决定?
圆的半径、
n°的圆心角所对 的弧长:
圆心角的度数.
C1 =
O
学习新知
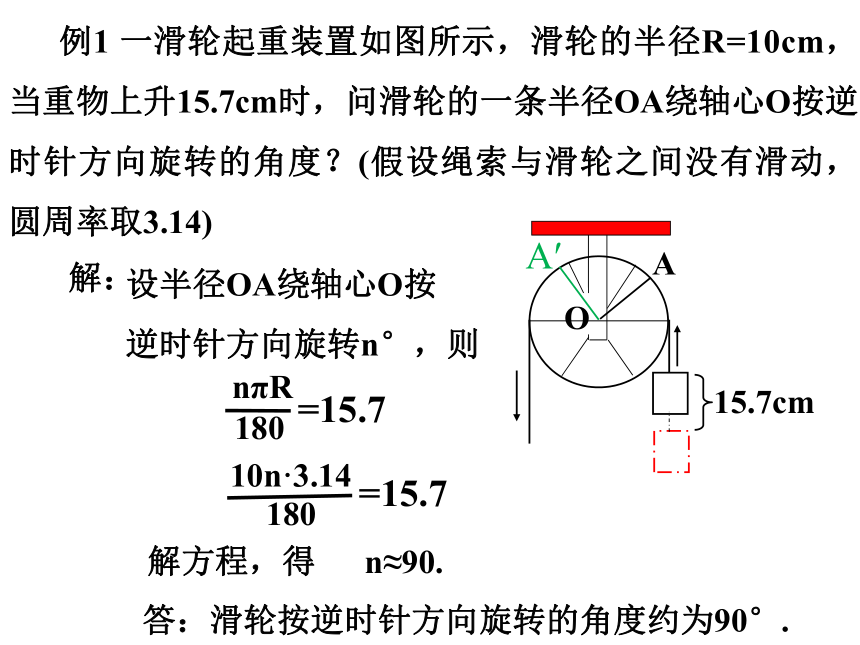
例1 一滑轮起重装置如图所示,滑轮的半径R=10cm,当重物上升15.7cm时,问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度?(假设绳索与滑轮之间没有滑动,圆周率取3.14)
A
15.7cm
A′
O
解:
解方程,得
答:滑轮按逆时针方向旋转的角度约为90°.
设半径OA绕轴心O按
逆时针方向旋转n°,则
n≈90.
nπR
180
=15.7
10n·3.14
180
=15.7
例2 古希腊埃拉托塞尼曾给出一个地球周长(或整个子午周长)的简单方法.如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α ,他实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
S
A
O
S
α
S
A
O
S
α
解:
∵太阳光线可看作平行的,
∴圆心角∠AOS=7.2°.
答:过南北极的地球周长约为39625km.
设地球的周长(即⊙O的周长)为C,则
∴C=
C
AS
(
=
360°
7.2°
=50.
50
AS
(
=50×5000
=250000(希腊里)
=39625(km)
=250000×0.1585km
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
A
B
O
n°
πR2
360°~
1°~
πR2
360
n°~
nπR2
360
学习新知
比较扇形面积公式 和弧长公式 ,你能用
弧长表示扇形面积吗?
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
l R
n°
解:
∴ AB的长度=
︵
120π×12
180
=
S扇形AOB=
nπR2
360
∵R=12cm,
nπR
180
=8π(cm)
120π×122
360
=
=48π(cm2)
n =120,
或S扇形=
1
2
×8π
×12
=48π(cm2)
∠AOB
1.已知:扇形AOB的半径为12cm,
求AB的长度和扇形AOB的面积.
︵
=120°,
练习巩固
2.已知:扇形的圆心角为120°,弧长为20π ,求扇形面积.
解:
∴ 20π=
120πR
180
∴S扇形=
nπR2
360
∵n=120°,
30
120π×302
360
=
=300π.
C1=20π ,
∴ R=
或S扇形=
1
2
×20π
×30
=300π.
例2 黄之涣在楼上要看到千里远.
鹳雀楼得有多高?
例题解析
O
B
在平面图形中,用什么图形可表示地球
A
P
如图,用⊙O 表示地球.
设点 O为地球球心,
BO为地球的半径,
BO=6370km.
用什么图形表示鹳雀楼?
用线段AB表示鹳雀楼.
设黄之涣在楼上的点 A看到千里远的点P.
显然AP是⊙O 的切线,
点 P为切点.
PB=500km.
︵
怎样求AB的长?
O
A
P
B
怎样求AB的长?
连接OP,
∵AP是⊙O 的切线,
∴OP⊥AP,
∠BOP=
求AB的长?
求AO的长?
O
A
P
B
连接OP,
∵AP是⊙O 的切线,
∴OP⊥AP.
PB= ,
︵
∵
180
n π R
∴n=
180 × 500
6370π
≈4.5.
即∠AOP=4.5°.
PB=500km,
︵
∵cos∠AOP=
OP
AO
∴AO=
=20(km).
cos4.5°
6370
=6390.
∴AB=AO-OB=6390-6370
要看到千里之外的远处,
要登上20km的高楼,可能吗?
(1)弧长和扇形面积公式是什么?你是如何得到
这两个公式的?如何运用?
(2)弧长与圆周长、扇形面积与圆面积之间有
什么联系?
课堂小结
1.一个扇形所在圆的半径为3cm,扇形的圆心角为120°,则扇形的面积是 cm2. (结果保留π)
3π
2. 120°的圆心角所对的弧长是12πcm,
则此弧所在的圆的半径是 cm.
18
练习巩固
4.如图,⊙O 是△ ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( ).
︵
B. C. D.
π
3
3
3
π
2
3
π
3
3
π
2
A
C
B
O
A
3.已知一个扇形的半径为6,且弧长是2π,则此扇形的圆心角为 ( ) .
A. 30° B. 60° C. 90° D.120°
B
今天作业
课本P57页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.7弧长和扇形面积(1)
教学目标:
理解 1°的圆心角所对的弧长等于圆周长的 ,
所对的扇形面积等于圆面积的 ;能够发现 n°
的圆心角所对的弧长和扇形面积都是 1°的圆心角
所对的弧长和扇形面积的 n 倍;能利用弧长表示扇
形面积.并能利用公式计算弧长和扇形面积.
课件说明
教学重点:
弧长和扇形面积公式的推导及运用.
我们知道,弧是圆的一部分,弧长就是圆周长的一部分.如何计算圆周长?如何计算弧长?
O
C=2πR
R
C1 =
复习旧知
(1)圆的周长可以看作是多少度的圆心角所对的弧长?
360°.
(2)在同圆或等圆中,每一个 1°的圆心角所对的
弧长有怎样的关系?
相等.
(3) 1°的圆心角所对的弧长是多少?
圆周长的 .
(4) n°的圆心角所对的弧长是多少?
是1°的圆心角所对弧长的 n 倍.
1
360
(5)怎样计算半径为 R 的圆中,1°的圆心角所对 的弧长?
1°的圆心角所对弧长是圆周长的 ,
为
.
(6)怎样计算半径为 R 的圆中,2°的圆心角所对 的弧长?
2°是 1°的 2 倍,所以弧长也是 1°的圆心角所对
弧长的 2 倍,为 .
2πR
360
=
πR
180
1
360
(7)怎样计算半径为 R 的圆中,5°的圆心角所对 的弧长?
5°是 1°的 5 倍,所以弧长也是 1°的圆心角所对
弧长的 5 倍,为 .
(8)怎样计算半径为 R 的圆中,n°的圆心角所对 的弧长?
n°是 1°的 n 倍,所以弧长也是 1°的圆心角所对
弧长的 n 倍,为 .
nπR
180
弧长的大小由哪些量决定?
圆的半径、
n°的圆心角所对 的弧长:
圆心角的度数.
C1 =
O
学习新知
例1 一滑轮起重装置如图所示,滑轮的半径R=10cm,当重物上升15.7cm时,问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度?(假设绳索与滑轮之间没有滑动,圆周率取3.14)
A
15.7cm
A′
O
解:
解方程,得
答:滑轮按逆时针方向旋转的角度约为90°.
设半径OA绕轴心O按
逆时针方向旋转n°,则
n≈90.
nπR
180
=15.7
10n·3.14
180
=15.7
例2 古希腊埃拉托塞尼曾给出一个地球周长(或整个子午周长)的简单方法.如图,点S和点A分别表示埃及的赛伊尼和亚历山大两地,亚历山大在赛伊尼的北方,两地的经度大致相同,两地的实际距离为5000希腊里(1希腊里≈158.5m).当太阳光线在赛伊尼直射时,同一时刻在亚历山大测量太阳光线偏离直射方向的角为α ,他实际测得α是7.2°,由此估算出了地球的周长,你能进行计算吗?
S
A
O
S
α
S
A
O
S
α
解:
∵太阳光线可看作平行的,
∴圆心角∠AOS=7.2°.
答:过南北极的地球周长约为39625km.
设地球的周长(即⊙O的周长)为C,则
∴C=
C
AS
(
=
360°
7.2°
=50.
50
AS
(
=50×5000
=250000(希腊里)
=39625(km)
=250000×0.1585km
由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形.
能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式?
A
B
O
n°
πR2
360°~
1°~
πR2
360
n°~
nπR2
360
学习新知
比较扇形面积公式 和弧长公式 ,你能用
弧长表示扇形面积吗?
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
l R
n°
解:
∴ AB的长度=
︵
120π×12
180
=
S扇形AOB=
nπR2
360
∵R=12cm,
nπR
180
=8π(cm)
120π×122
360
=
=48π(cm2)
n =120,
或S扇形=
1
2
×8π
×12
=48π(cm2)
∠AOB
1.已知:扇形AOB的半径为12cm,
求AB的长度和扇形AOB的面积.
︵
=120°,
练习巩固
2.已知:扇形的圆心角为120°,弧长为20π ,求扇形面积.
解:
∴ 20π=
120πR
180
∴S扇形=
nπR2
360
∵n=120°,
30
120π×302
360
=
=300π.
C1=20π ,
∴ R=
或S扇形=
1
2
×20π
×30
=300π.
例2 黄之涣在楼上要看到千里远.
鹳雀楼得有多高?
例题解析
O
B
在平面图形中,用什么图形可表示地球
A
P
如图,用⊙O 表示地球.
设点 O为地球球心,
BO为地球的半径,
BO=6370km.
用什么图形表示鹳雀楼?
用线段AB表示鹳雀楼.
设黄之涣在楼上的点 A看到千里远的点P.
显然AP是⊙O 的切线,
点 P为切点.
PB=500km.
︵
怎样求AB的长?
O
A
P
B
怎样求AB的长?
连接OP,
∵AP是⊙O 的切线,
∴OP⊥AP,
∠BOP=
求AB的长?
求AO的长?
O
A
P
B
连接OP,
∵AP是⊙O 的切线,
∴OP⊥AP.
PB= ,
︵
∵
180
n π R
∴n=
180 × 500
6370π
≈4.5.
即∠AOP=4.5°.
PB=500km,
︵
∵cos∠AOP=
OP
AO
∴AO=
=20(km).
cos4.5°
6370
=6390.
∴AB=AO-OB=6390-6370
要看到千里之外的远处,
要登上20km的高楼,可能吗?
(1)弧长和扇形面积公式是什么?你是如何得到
这两个公式的?如何运用?
(2)弧长与圆周长、扇形面积与圆面积之间有
什么联系?
课堂小结
1.一个扇形所在圆的半径为3cm,扇形的圆心角为120°,则扇形的面积是 cm2. (结果保留π)
3π
2. 120°的圆心角所对的弧长是12πcm,
则此弧所在的圆的半径是 cm.
18
练习巩固
4.如图,⊙O 是△ ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC的长等于( ).
︵
B. C. D.
π
3
3
3
π
2
3
π
3
3
π
2
A
C
B
O
A
3.已知一个扇形的半径为6,且弧长是2π,则此扇形的圆心角为 ( ) .
A. 30° B. 60° C. 90° D.120°
B
今天作业
课本P57页第1、2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
