26.3 用频率估计概率(1)课件 (共25张PPT)
文档属性
| 名称 | 26.3 用频率估计概率(1)课件 (共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 19:38:59 | ||
图片预览






文档简介
(共25张PPT)
沪科版 九年级下册
26.3用频率估计概率(1)
本课是在学生已经学习了用列举法求概率的基础上,进一步研究用频率估计概率.
课件说明
教学目标:
用频率估计概率.
教学重点:
用频率估计概率.
1.用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.而事件A出现的
结果有m个,则事件A的概率为:
复习旧知
2.抛一枚质地均匀的硬币,正面向上的概率是
多少?你是怎么求出来的?
P(A)=
m
n
3.什么叫频数?频率?如何求频率?
频数表示某一对象出现的次数;
频率是某一对象的频数与总次数的比值,
它们都反映了各个对象出现的频繁程度.
复习旧知
阅读课本104--106页,解决以下问题:
1.课本的实例能用以前的方法求它的概率吗?
2.根据硬币频率分布表绘制抛币频率折线图,
有何发现?
3. 分析数学家大量重复试验数据,有何发现?
4.分析发芽种子的频率和乒乓球优等品的频率,
你有何发现?
5.可以用频率估计概率吗?
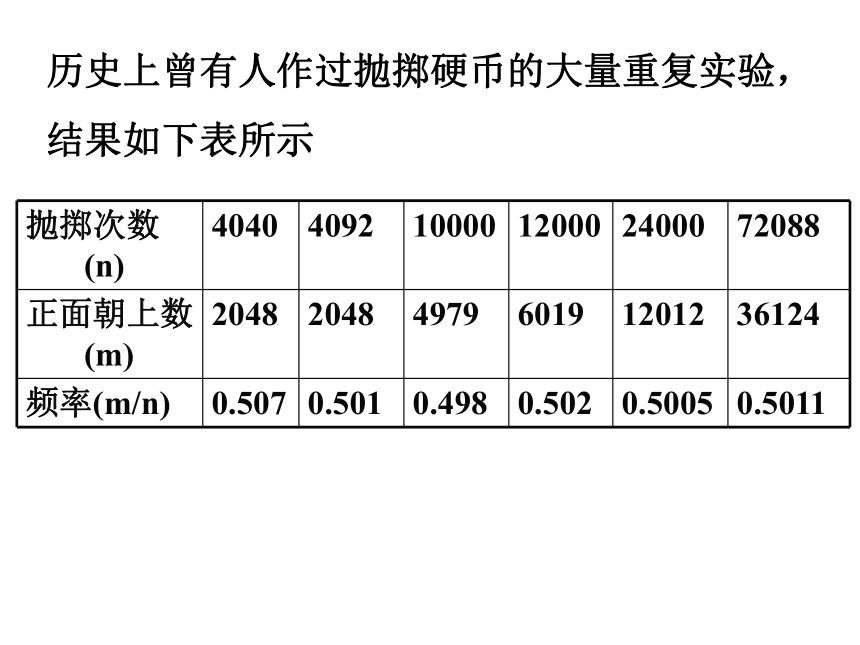
抛掷次数
(n) 4040 4092 10000 12000 24000 72088
正面朝上数
(m) 2048 2048 4979 6019 12012 36124
频率(m/n) 0.507 0.501 0.498 0.502 0.5005 0.5011
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示
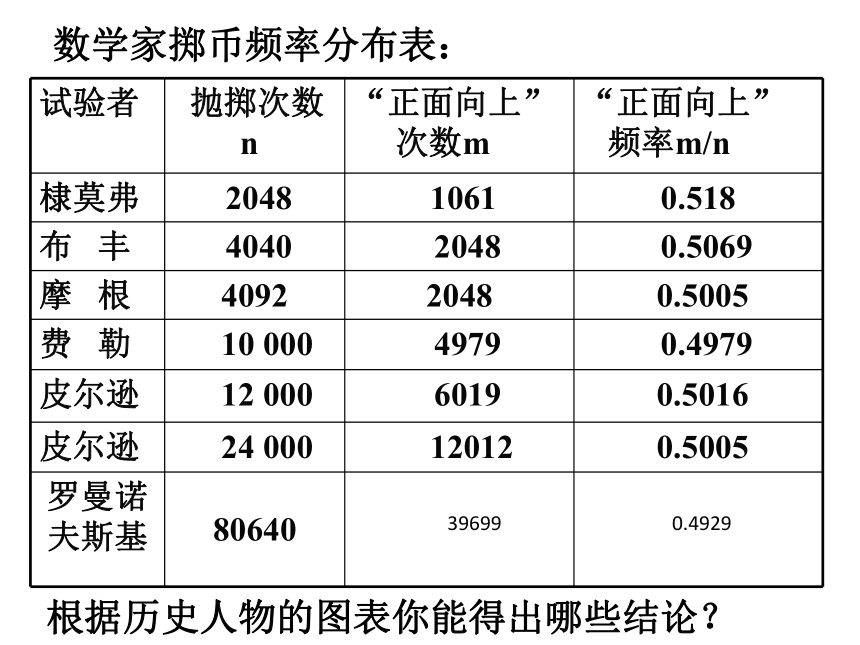
试验者 抛掷次数
n “正面向上”
次数m “正面向上”
频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
摩 根 4092 2048 0.5005
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
罗曼诺夫斯基
80640
数学家掷币频率分布表:
根据历史人物的图表你能得出哪些结论?
39699
0.4929
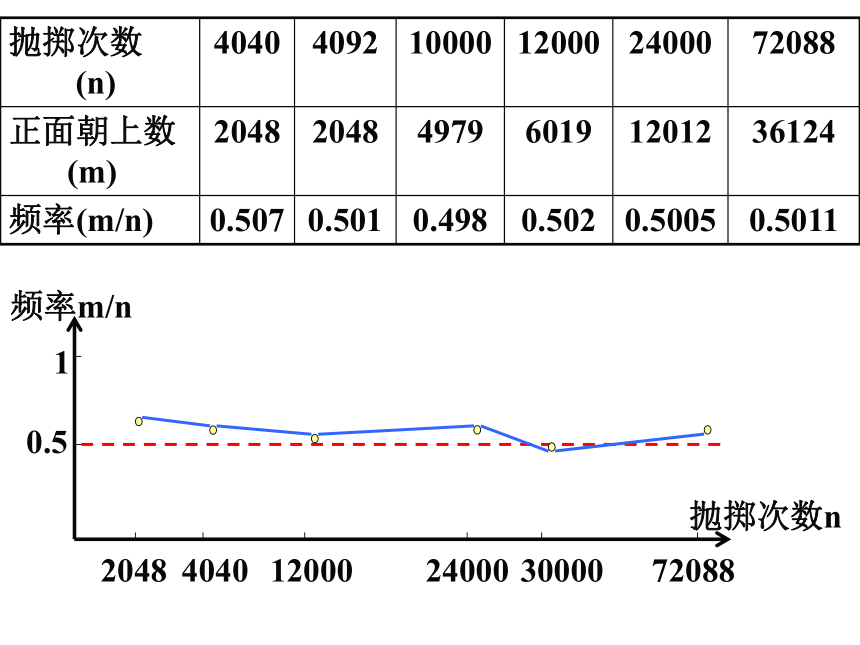
抛掷次数
(n) 4040 4092 10000 12000 24000 72088
正面朝上数
(m) 2048 2048 4979 6019 12012 36124
频率(m/n) 0.507 0.501 0.498 0.502 0.5005 0.5011
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
随着抛掷次数的增加,“正面向上”的频率在哪个数字的左右摆动?
当“正面向上”的频率逐渐稳定到0. 5时,“反面向上”的频率呈现什么规律?概率与频率稳定值的关系是什么呢?
这个稳定性的频率就反映了该随机事件的概率.
1.某种油菜籽在相同条件下的发芽试验结果表:
当试验的油菜籽的粒数很多时,油菜籽发芽的
频率 接近于常数 ,在它附近摆动.
0.9
m
n
2.某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率 接近于常数 ,在它附近摆动.
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数m
抽取球数n
0.95
分析材料1,2,你有何发现?
m
n
当实验的所有结果不是有限个,或结果的个数很多,或各种可能结果发生的可能性不相等时,很难用列表或树状图求该事件发生的概率.
归纳:
在随机现象中,一个随机事件发生与否,事先无法预料,表面上看似无规律可循,但当我们做大量重复实验时,这个事件发生的频率呈稳定性,这个稳定性的频率就反映了该随机事件的概率。由此我们可以得到概率的另一定义:
一般地,在大量重复试验下,随机事件A发生的频率 会稳定在某个常数p附近.于是我们用一个事件发生的稳定频率 p 来估计这一事件发生的概率即:P(A)=p
说明:我们不但能用前面的等可能事件的概率公式去求一个事件的概率,而且还可以用大量重复试验的方法去计算一组数据的频率,用一组事件发生的频率的稳定值去估计这一事件的概率.
概率的定义:
m
n
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
练习1 对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数
m
42
88
176
445
724
901
优等品频率
m/n
0.84
0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是 .
抽取衬衫2000件,约有 件优质品.
0.9
1800
练习2 某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心
次数m
13
58
104
255
400
击中靶心
频率m/n
(1)这个射手射击一次,击中靶心的概率是 .
0.5
(2)这射手射击1600次,击中靶心的次数是 .
800
0.65
0.58
0.52
0.51
0.50
(1)我们学习了哪几种求随机事件概率的方法?
(2)结合你的生活经验,说说你对频率与概率
之间关系的认识.
课堂小结
1.当重复试验次数足够多时,可用频率来估计
概率.历史上数学家皮尔逊(Pearson)曾在实
验中掷均匀的硬币24000次,正面朝上的次
数是12012次,频率约为0.5,则掷一枚均匀
的硬币,正面朝上的概率是 ·
巩固新知
0.5
2.某射击运动员在同一条件下的射击成绩记录
如下表.
根据频率的稳定性,估计这名运动员射击1次时“射中九环以上”的概率是( ).
A.0.90 B.0.82 C.0.85 D. 0.84
射击次数 20 80 100 200 400 1000
“射中九环以上”的数据 18 68 82 168 327 823
“射中九环以上”的频率 0.90 0.85 0.82 0.84 0.82 0.82
B
3.某小组做一个“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如下的折线统计图,则符合 这一结果的试验可能是( ).
A.抛一枚硬币,出现正面朝上
B.掷一枚正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,
从中任抽1张牌的花色是红桃
D.从一个装有2个红球、1个黑球的
袋子中任取1个球,取到的是黑球
100
200
300
次数
0
0.1
0.2
0.3
0.4
频率
D
4.在一个不透明的袋中装有若干个材质、大小
完全相同的红球,小明在袋中放入3个黑球
(每个黑球除颜色外其余都与红球相同),摇匀
后每次随机从袋中摸出一个球,记录颜色后
放回袋中,通过大量重复摸球试验后发现,
摸到红球的频率稳定在 0.85左右,估计袋中
红球有 个.
17
5.一个不透明袋子中装有白球和黑球若50个,
这些球除颜色外其他都相同.从袋中随机摸
出1个球,记下其颜色后放回、搅匀,不断
重复上述过程,获得试验数据如下表:
则估计摸到白球的概率是 (精确到 0.1),
由此估计黑球有 个.
摸球次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 480 600 1800
摸到白球的频m/n 0.65 0.62 0.593 0.604 0.6 0.6 0.6
0.6
20
今天作业
课本P108页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
26.3用频率估计概率(1)
本课是在学生已经学习了用列举法求概率的基础上,进一步研究用频率估计概率.
课件说明
教学目标:
用频率估计概率.
教学重点:
用频率估计概率.
1.用列举法求概率的条件是什么
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.而事件A出现的
结果有m个,则事件A的概率为:
复习旧知
2.抛一枚质地均匀的硬币,正面向上的概率是
多少?你是怎么求出来的?
P(A)=
m
n
3.什么叫频数?频率?如何求频率?
频数表示某一对象出现的次数;
频率是某一对象的频数与总次数的比值,
它们都反映了各个对象出现的频繁程度.
复习旧知
阅读课本104--106页,解决以下问题:
1.课本的实例能用以前的方法求它的概率吗?
2.根据硬币频率分布表绘制抛币频率折线图,
有何发现?
3. 分析数学家大量重复试验数据,有何发现?
4.分析发芽种子的频率和乒乓球优等品的频率,
你有何发现?
5.可以用频率估计概率吗?
抛掷次数
(n) 4040 4092 10000 12000 24000 72088
正面朝上数
(m) 2048 2048 4979 6019 12012 36124
频率(m/n) 0.507 0.501 0.498 0.502 0.5005 0.5011
历史上曾有人作过抛掷硬币的大量重复实验,
结果如下表所示
试验者 抛掷次数
n “正面向上”
次数m “正面向上”
频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
摩 根 4092 2048 0.5005
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
罗曼诺夫斯基
80640
数学家掷币频率分布表:
根据历史人物的图表你能得出哪些结论?
39699
0.4929
抛掷次数
(n) 4040 4092 10000 12000 24000 72088
正面朝上数
(m) 2048 2048 4979 6019 12012 36124
频率(m/n) 0.507 0.501 0.498 0.502 0.5005 0.5011
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
随着抛掷次数的增加,“正面向上”的频率在哪个数字的左右摆动?
当“正面向上”的频率逐渐稳定到0. 5时,“反面向上”的频率呈现什么规律?概率与频率稳定值的关系是什么呢?
这个稳定性的频率就反映了该随机事件的概率.
1.某种油菜籽在相同条件下的发芽试验结果表:
当试验的油菜籽的粒数很多时,油菜籽发芽的
频率 接近于常数 ,在它附近摆动.
0.9
m
n
2.某批乒乓球产品质量检查结果表:
当抽查的球数很多时,抽到优等品的频率 接近于常数 ,在它附近摆动.
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率
2000
1000
500
200
100
50
1902
954
470
194
92
45
优等品数m
抽取球数n
0.95
分析材料1,2,你有何发现?
m
n
当实验的所有结果不是有限个,或结果的个数很多,或各种可能结果发生的可能性不相等时,很难用列表或树状图求该事件发生的概率.
归纳:
在随机现象中,一个随机事件发生与否,事先无法预料,表面上看似无规律可循,但当我们做大量重复实验时,这个事件发生的频率呈稳定性,这个稳定性的频率就反映了该随机事件的概率。由此我们可以得到概率的另一定义:
一般地,在大量重复试验下,随机事件A发生的频率 会稳定在某个常数p附近.于是我们用一个事件发生的稳定频率 p 来估计这一事件发生的概率即:P(A)=p
说明:我们不但能用前面的等可能事件的概率公式去求一个事件的概率,而且还可以用大量重复试验的方法去计算一组数据的频率,用一组事件发生的频率的稳定值去估计这一事件的概率.
概率的定义:
m
n
人们在长期的实践中发现,在随机试验中,由于众多微小的偶然因素的影响,每次测得的结果虽不尽相同,但大量重复试验所得结果却能反应客观规律.这称为大数法则,亦称大数定律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
练习1 对一批衬衫进行抽查,结果如下表:
抽取件数n 50 100 200 500 800 1000
优等品件数
m
42
88
176
445
724
901
优等品频率
m/n
0.84
0.88
0.88
0.89
0.901
0.905
求抽取一件衬衫是优等品的概率约是 .
抽取衬衫2000件,约有 件优质品.
0.9
1800
练习2 某射手进行射击,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心
次数m
13
58
104
255
400
击中靶心
频率m/n
(1)这个射手射击一次,击中靶心的概率是 .
0.5
(2)这射手射击1600次,击中靶心的次数是 .
800
0.65
0.58
0.52
0.51
0.50
(1)我们学习了哪几种求随机事件概率的方法?
(2)结合你的生活经验,说说你对频率与概率
之间关系的认识.
课堂小结
1.当重复试验次数足够多时,可用频率来估计
概率.历史上数学家皮尔逊(Pearson)曾在实
验中掷均匀的硬币24000次,正面朝上的次
数是12012次,频率约为0.5,则掷一枚均匀
的硬币,正面朝上的概率是 ·
巩固新知
0.5
2.某射击运动员在同一条件下的射击成绩记录
如下表.
根据频率的稳定性,估计这名运动员射击1次时“射中九环以上”的概率是( ).
A.0.90 B.0.82 C.0.85 D. 0.84
射击次数 20 80 100 200 400 1000
“射中九环以上”的数据 18 68 82 168 327 823
“射中九环以上”的频率 0.90 0.85 0.82 0.84 0.82 0.82
B
3.某小组做一个“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如下的折线统计图,则符合 这一结果的试验可能是( ).
A.抛一枚硬币,出现正面朝上
B.掷一枚正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,
从中任抽1张牌的花色是红桃
D.从一个装有2个红球、1个黑球的
袋子中任取1个球,取到的是黑球
100
200
300
次数
0
0.1
0.2
0.3
0.4
频率
D
4.在一个不透明的袋中装有若干个材质、大小
完全相同的红球,小明在袋中放入3个黑球
(每个黑球除颜色外其余都与红球相同),摇匀
后每次随机从袋中摸出一个球,记录颜色后
放回袋中,通过大量重复摸球试验后发现,
摸到红球的频率稳定在 0.85左右,估计袋中
红球有 个.
17
5.一个不透明袋子中装有白球和黑球若50个,
这些球除颜色外其他都相同.从袋中随机摸
出1个球,记下其颜色后放回、搅匀,不断
重复上述过程,获得试验数据如下表:
则估计摸到白球的概率是 (精确到 0.1),
由此估计黑球有 个.
摸球次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 480 600 1800
摸到白球的频m/n 0.65 0.62 0.593 0.604 0.6 0.6 0.6
0.6
20
今天作业
课本P108页第3、4题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
