24.7 弧长与扇形面积(2)课件 (共26张PPT)
文档属性
| 名称 | 24.7 弧长与扇形面积(2)课件 (共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 19:38:14 | ||
图片预览


文档简介
(共26张PPT)
沪科版 九年级下册
24.7弧长与扇形面积(2)
教学目标:
1.了解圆锥及其母线、侧面积、全面积等概念,会
计算圆锥的侧面积和全面积;
2.通过本节课的学习,学会观察、归纳的学习方法,
培养空间想象能力.
教学重点:
圆锥的侧面积和全面积的计算.
课件说明
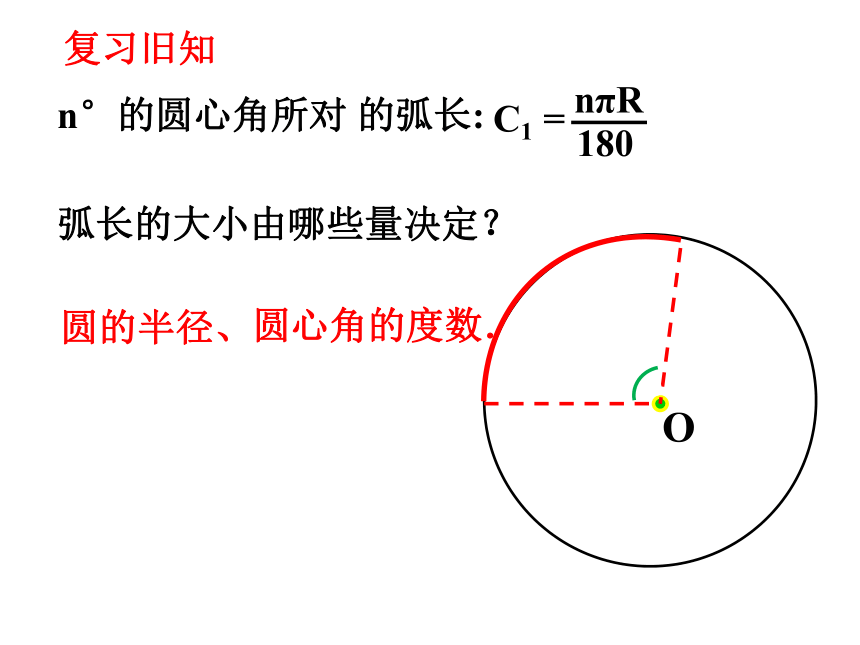
弧长的大小由哪些量决定?
圆的半径、
n°的圆心角所对 的弧长:
圆心角的度数.
C1 =
O
nπR
180
复习旧知
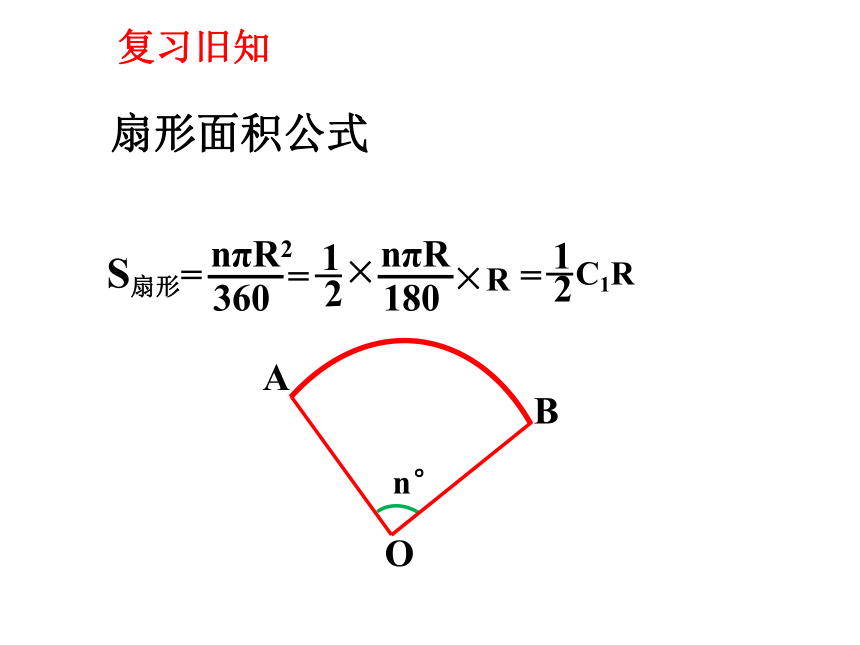
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
C1R
n°
nπR
180
nπR2
360
扇形面积公式
复习旧知
展开
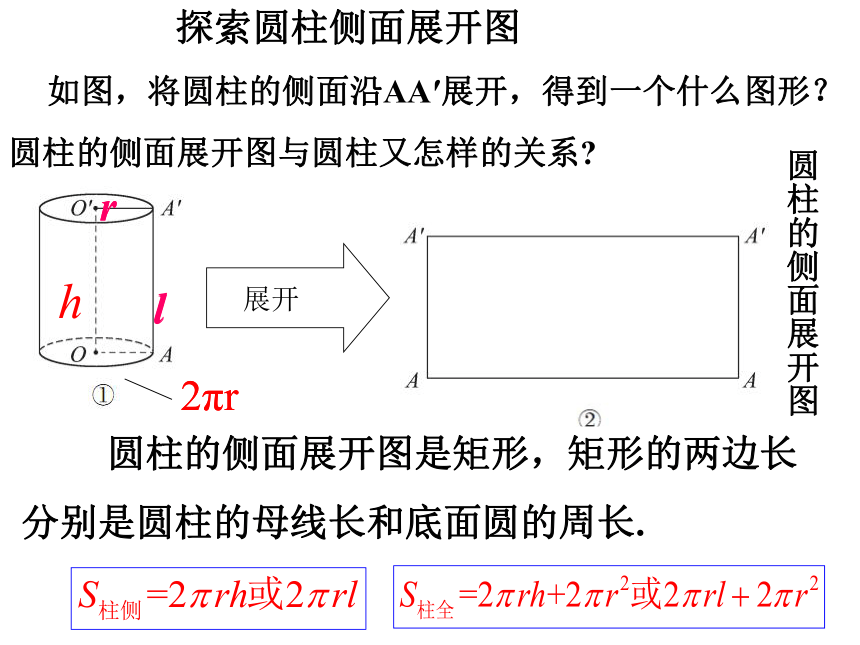
圆柱的侧面展开图
如图,将圆柱的侧面沿AA′展开,得到一个什么图形?圆柱的侧面展开图与圆柱又怎样的关系
r
l
l
圆柱的侧面展开图是矩形,矩形的两边长
分别是圆柱的母线长和底面圆的周长.
r
2πr
2πr
探索圆柱侧面展开图
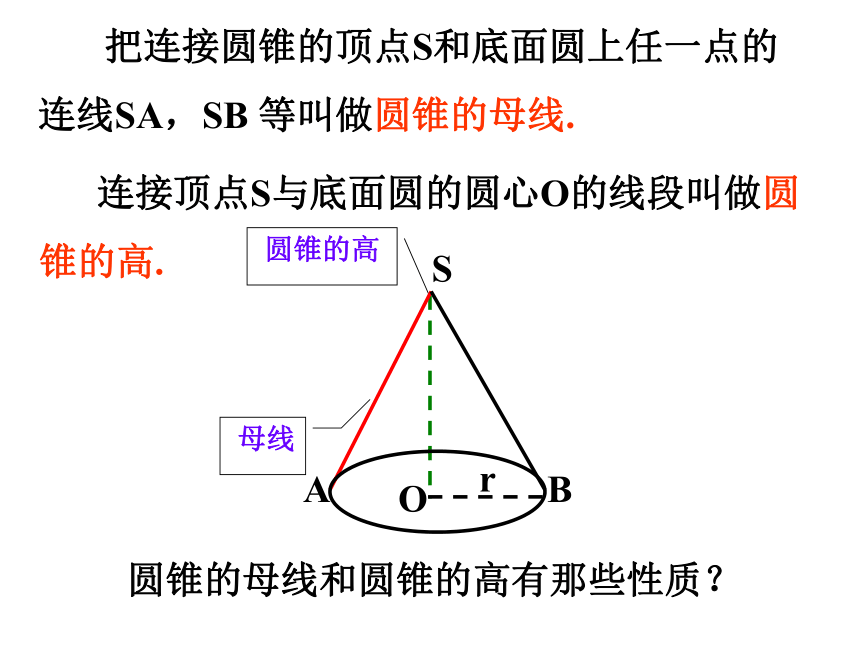
圆锥的高
母线
S
A
O
B
r
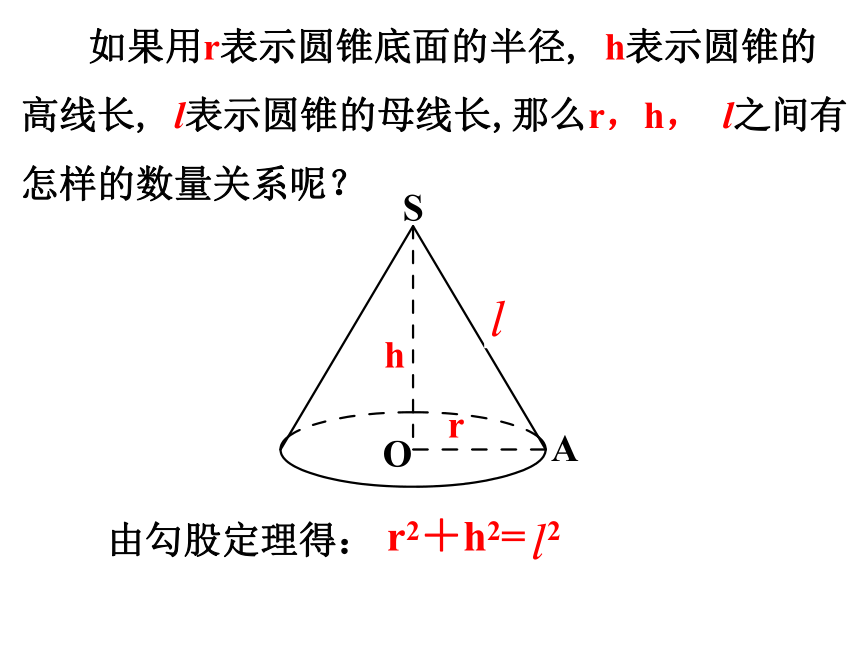
把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
连接顶点S与底面圆的圆心O的线段叫做圆锥的高.
圆锥的母线和圆锥的高有那些性质?
h
r
由勾股定理得:
r2+h2= 2
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r,h, l之间有怎样的数量关系呢?
O
S
A
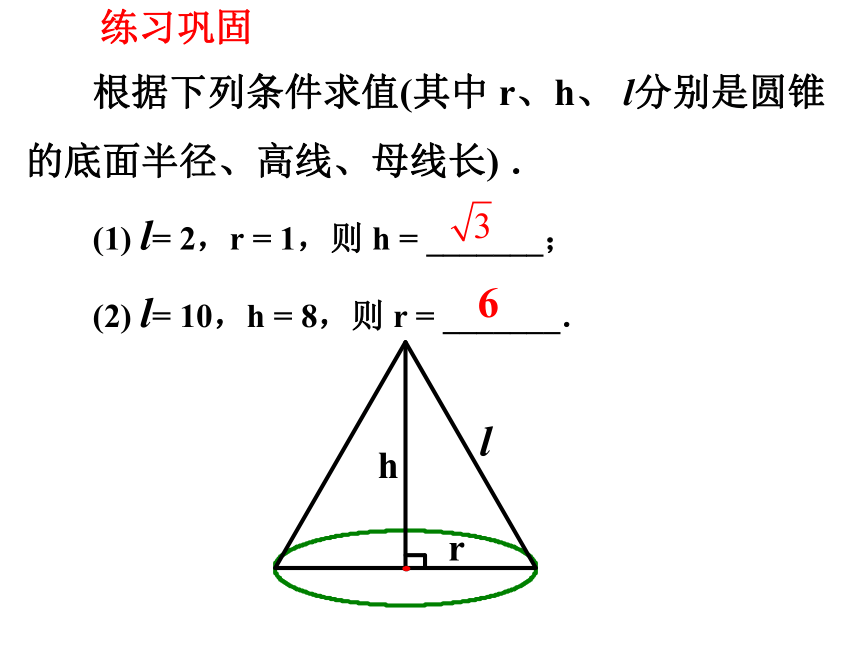
根据下列条件求值(其中 r、h、 l分别是圆锥的底面半径、高线、母线长) .
(1) l= 2,r = 1,则 h = _______;
(2) l= 10,h = 8,则 r = _______.
r
h
l
6
练习巩固
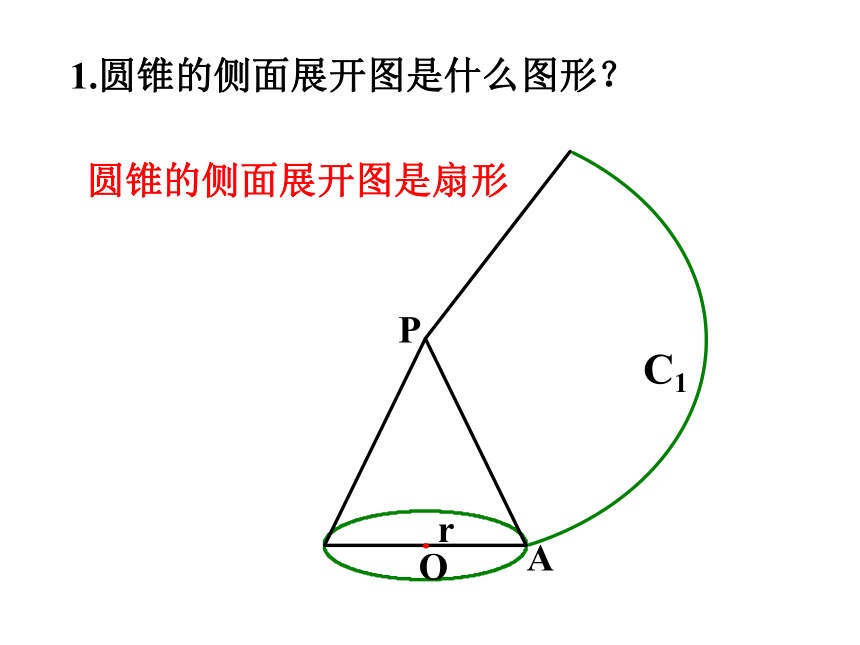
1.圆锥的侧面展开图是什么图形?
O
A
P
r
C1
圆锥的侧面展开图是扇形
2.圆锥的侧面展开图中的等量关系
O
A
P
r
l
圆锥侧面展开图扇形的半径 =
侧面展开图扇形的弧长=
C1
圆锥母线的长l
R
l
圆锥的底面周长
=2πr
3.如何计算圆锥的侧面积?
O
A
S
r
l
C1
∴ S 侧 = πrl
(r表示圆锥底面的半径, l表示圆锥的母线长 )
∴
∵
S扇形=
C1l,
1
2
R
S侧=
C1l,
1
2
C1
=2πr,
S侧=
l,
1
2
2πr
4.如何计算圆锥的全面积?
O
A
S
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积.
=πr(r+l)
例3 如图,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
例题解析
烟囱帽的侧面展开图是扇形,
解:
如右图,
3.展开图中扇形的半径相当于烟囱帽的什么?
2.要画出一个扇形,需要知道什么条件?
1.烟囱帽的侧面展开图是什么图形?
扇形.
要知道扇形的半径与弧长
4.展开图中扇形的弧长相当于烟囱帽的什么?
扇形的弧长
扇形的半径
例3 如图,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
烟囱帽的侧面展开图是扇形,
解:
如右图,
∵ C1=80π,
∴ S扇形=
C1
1
2
1
2
=
×80π
×50
=2000π(cm2)
l
l=50,
1.已知:把圆锥的侧面展开得到扇形,其半径OA=3,圆心角∠AOB=120°,求AB的长度.
︵
解:
∴ AB的长度=
︵
120π×3
180
=
∵R=3,
nπR
180
=2π.
n =120,
A
B
O
120°
O
A
B
C
D
2.如图,圆柱形排水管道的截面半径OC=
0.6 m,水面高DC= 0.3 m,求截面上有水部分的面积.
如何求它的面积?
S截面=
S扇形OACB
-S△OAB
∠AOB=?°
AB=?
O
A
B
C
D
∴ S截面=
S扇形OAB
-S△OAB
连接 OA ,OB.
作 OC⊥AB ,垂足为D .
解:
OC交AB于点C.
︵
连接 AC
∵OC=0.6m,
DC=0.3m,
∴OD=OC-DC=0.3m.
∴OD=DC.
∴AC=AO,
∴AB是OC的垂直平分线,
∴AC=AO=OC=0.6m。
∴∠AOC=60°,
∴∠AOB=120°.
=
∴AD=
∴AB=
AO2-OD2
3 ,
0.3
3 .
0.6
120π×0.62
360
=
-
0.3
1
2
×
3
0.6
≈0.22( m2).
(1)圆锥的侧面展开图是什么形状?
(2)如何利用圆锥的侧面展开图求得其侧面积,
进而得到其全面积?
课堂小结
O
A
B
C
D
E
F
1.如图,已知⊙O是正六边形ABCDEF的外接圆,AB的长为 ,
2
3
则阴影部分的
面积是 .
π
︵
练习巩固
3
-
2
3
π
2.如图,AC⊥BC,AC=BC=4.以AC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
︵
A
B
E
O
C
D
3
2
-
5
3
π
4.如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°, 则此圆锥高OC 的长度是 .
5
2
3.扇形的半径为3,且圆心角为60°,则此扇形的弧长是( ) .
A. B. C. D.
1
2
π
π
3
2
π
2π
B
A
B
C
D
5.如图,四边形ABCD是平行四边形,
∠A=2∠B, ⊙C的半径是3cm ,则图中的阴影面积为 .
3πcm2
今天作业
课本P57页第3、4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 九年级下册
24.7弧长与扇形面积(2)
教学目标:
1.了解圆锥及其母线、侧面积、全面积等概念,会
计算圆锥的侧面积和全面积;
2.通过本节课的学习,学会观察、归纳的学习方法,
培养空间想象能力.
教学重点:
圆锥的侧面积和全面积的计算.
课件说明
弧长的大小由哪些量决定?
圆的半径、
n°的圆心角所对 的弧长:
圆心角的度数.
C1 =
O
nπR
180
复习旧知
A
B
O
S扇形=
=
1
2
×
×R
=
1
2
C1R
n°
nπR
180
nπR2
360
扇形面积公式
复习旧知
展开
圆柱的侧面展开图
如图,将圆柱的侧面沿AA′展开,得到一个什么图形?圆柱的侧面展开图与圆柱又怎样的关系
r
l
l
圆柱的侧面展开图是矩形,矩形的两边长
分别是圆柱的母线长和底面圆的周长.
r
2πr
2πr
探索圆柱侧面展开图
圆锥的高
母线
S
A
O
B
r
把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
连接顶点S与底面圆的圆心O的线段叫做圆锥的高.
圆锥的母线和圆锥的高有那些性质?
h
r
由勾股定理得:
r2+h2= 2
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r,h, l之间有怎样的数量关系呢?
O
S
A
根据下列条件求值(其中 r、h、 l分别是圆锥的底面半径、高线、母线长) .
(1) l= 2,r = 1,则 h = _______;
(2) l= 10,h = 8,则 r = _______.
r
h
l
6
练习巩固
1.圆锥的侧面展开图是什么图形?
O
A
P
r
C1
圆锥的侧面展开图是扇形
2.圆锥的侧面展开图中的等量关系
O
A
P
r
l
圆锥侧面展开图扇形的半径 =
侧面展开图扇形的弧长=
C1
圆锥母线的长l
R
l
圆锥的底面周长
=2πr
3.如何计算圆锥的侧面积?
O
A
S
r
l
C1
∴ S 侧 = πrl
(r表示圆锥底面的半径, l表示圆锥的母线长 )
∴
∵
S扇形=
C1l,
1
2
R
S侧=
C1l,
1
2
C1
=2πr,
S侧=
l,
1
2
2πr
4.如何计算圆锥的全面积?
O
A
S
r
l
圆锥的侧面积与底面积的和叫做圆锥的全面积.
=πr(r+l)
例3 如图,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
例题解析
烟囱帽的侧面展开图是扇形,
解:
如右图,
3.展开图中扇形的半径相当于烟囱帽的什么?
2.要画出一个扇形,需要知道什么条件?
1.烟囱帽的侧面展开图是什么图形?
扇形.
要知道扇形的半径与弧长
4.展开图中扇形的弧长相当于烟囱帽的什么?
扇形的弧长
扇形的半径
例3 如图,圆锥形的烟囱帽,它的底面直径为80cm,母线为50cm.在一块大铁皮上剪裁时,如何画出这个烟囱帽的侧面展开图?求出该侧面展开图的面积.
烟囱帽的侧面展开图是扇形,
解:
如右图,
∵ C1=80π,
∴ S扇形=
C1
1
2
1
2
=
×80π
×50
=2000π(cm2)
l
l=50,
1.已知:把圆锥的侧面展开得到扇形,其半径OA=3,圆心角∠AOB=120°,求AB的长度.
︵
解:
∴ AB的长度=
︵
120π×3
180
=
∵R=3,
nπR
180
=2π.
n =120,
A
B
O
120°
O
A
B
C
D
2.如图,圆柱形排水管道的截面半径OC=
0.6 m,水面高DC= 0.3 m,求截面上有水部分的面积.
如何求它的面积?
S截面=
S扇形OACB
-S△OAB
∠AOB=?°
AB=?
O
A
B
C
D
∴ S截面=
S扇形OAB
-S△OAB
连接 OA ,OB.
作 OC⊥AB ,垂足为D .
解:
OC交AB于点C.
︵
连接 AC
∵OC=0.6m,
DC=0.3m,
∴OD=OC-DC=0.3m.
∴OD=DC.
∴AC=AO,
∴AB是OC的垂直平分线,
∴AC=AO=OC=0.6m。
∴∠AOC=60°,
∴∠AOB=120°.
=
∴AD=
∴AB=
AO2-OD2
3 ,
0.3
3 .
0.6
120π×0.62
360
=
-
0.3
1
2
×
3
0.6
≈0.22( m2).
(1)圆锥的侧面展开图是什么形状?
(2)如何利用圆锥的侧面展开图求得其侧面积,
进而得到其全面积?
课堂小结
O
A
B
C
D
E
F
1.如图,已知⊙O是正六边形ABCDEF的外接圆,AB的长为 ,
2
3
则阴影部分的
面积是 .
π
︵
练习巩固
3
-
2
3
π
2.如图,AC⊥BC,AC=BC=4.以AC为直径作半圆,圆心为点O,以点C为圆心,BC为半径作AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是 .
︵
A
B
E
O
C
D
3
2
-
5
3
π
4.如图,圆锥侧面展开得到扇形,此扇形半径 CA=6,圆心角∠ACB=120°, 则此圆锥高OC 的长度是 .
5
2
3.扇形的半径为3,且圆心角为60°,则此扇形的弧长是( ) .
A. B. C. D.
1
2
π
π
3
2
π
2π
B
A
B
C
D
5.如图,四边形ABCD是平行四边形,
∠A=2∠B, ⊙C的半径是3cm ,则图中的阴影面积为 .
3πcm2
今天作业
课本P57页第3、4、5题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
