北师大版八年级数学上册第一章《勾股定理》测试卷(含答案)
文档属性
| 名称 | 北师大版八年级数学上册第一章《勾股定理》测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-05 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版八年级数学上册第一章测试卷(含答案)
学校; 班级: 姓名: 评分:
一、选择题(每小题3分,共30分)
1、下列四组数中不能构成直角三角形的一组是 ( )
A.4,5,6 B.7,24,25 C.5,12,13 D.1,2,
2、下列说法中正确的是 ( )
A.已知a,b,c是三角形的三边,则
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以
D.在Rt△ABC中,∠B=90°,所以
3、如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,
折痕为MN,则线段CN长是( )
A.3cm B.4cm C.5cm D.6cm
4、如图,已知正方形B的面积为144,如果正方形C的面积为169,那么正方形A的面积为( )
A.313 B.144 C.169 D.25
第3题图
5、如图,在Rt△ABC中,∠ACB=90°,若AC=5 cm,BC=12 cm,则斜边上的高CD的长为( )
A.6 cm B.8.5 cm C.cm D.cm
6、如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
7、在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8、如果三角形的三边5,m,n满足(m+n)(m-n)=25,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
9、如果一个三角形的三边长a,b,c满足a2+b2+c2+338=10a+24b+26c,那么这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,已知a∶b=3∶4,c=10,则
△ABC的面积为( )
A.24 B.12 C.28 D.30
二、填空题(每小题4分,共28分)
11、在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2= .
12、把一根12厘米长的铁丝,从一端起顺次截下3厘米和5厘米的两根铁丝,用这三条铁丝摆成的三角形是 .
13、已知,则由x,y,z为三边的三角形是 .
14、如图,某会展中心在会展期间准备将高5 m,长13 m,宽2 m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要________元钱.
第15题图
15、(2015·湖南株洲中考) 如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于 .
16、如题16图,有一圆柱,其高为8cm,它的底面半径2cm,在
下底面点A处有一只蚂蚁,它想得到上底面与点A相对的点
B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程
为 cm(注:π取3).
17、在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,
则△ABC的面积为 cm2 .
三、解答题(共62分)
18、(5分)如图,EF是正方形两对边中点的连线段,将∠A沿DK折叠,使它的顶点A落在EF上的 G点,求∠DKG的度数.
19、(5分)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
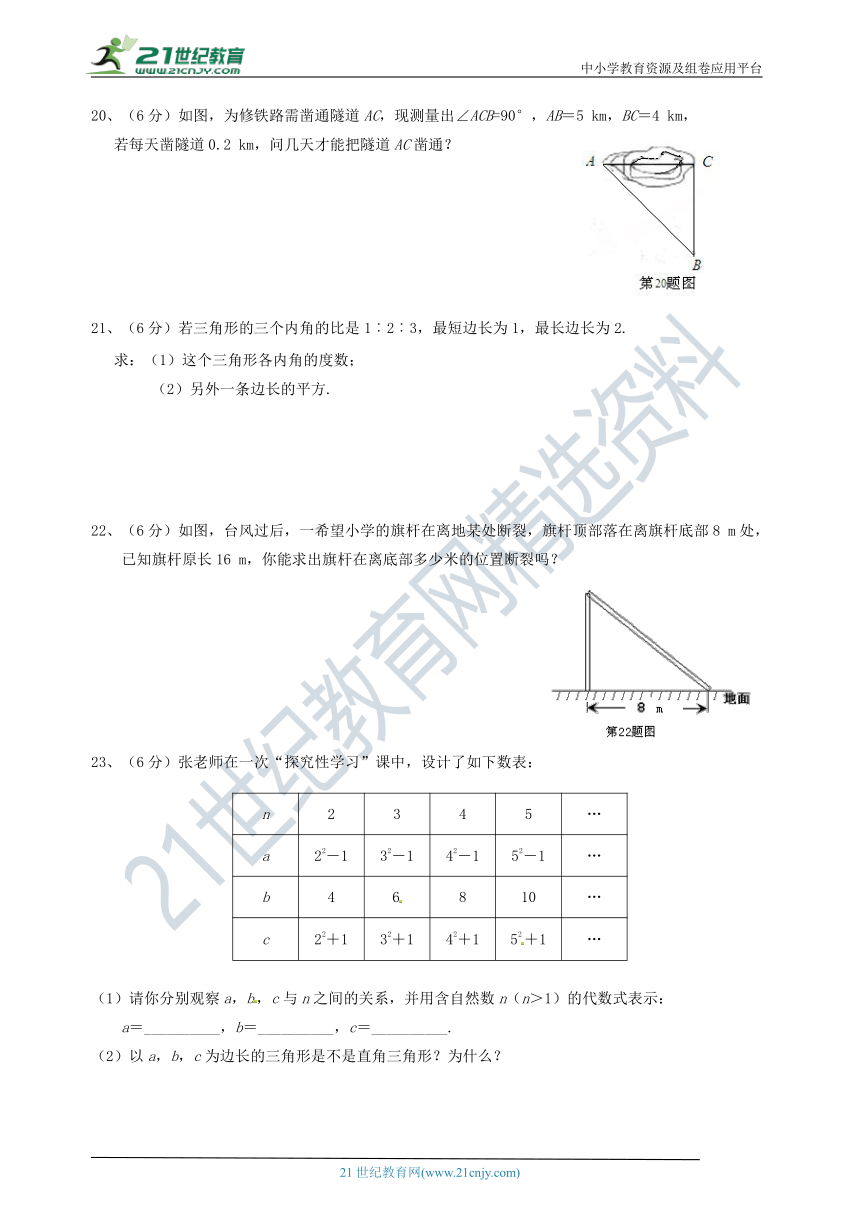
20、(6分)如图,为修铁路需凿通隧道AC,现测量出∠ACB=90°,AB=5 km,BC=4 km,
若每天凿隧道0.2 km,问几天才能把隧道AC凿通?
21、(6分)若三角形的三个内角的比是1︰2︰3,最短边长为1,最长边长为2.
求:(1)这个三角形各内角的度数;
(2)另外一条边长的平方.
22、(6分)如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8 m处,已知旗杆原长16 m,你能求出旗杆在离底部多少米的位置断裂吗?
23、(6分)张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__________,b=__________,c=__________.
(2)以a,b,c为边长的三角形是不是直角三角形?为什么?
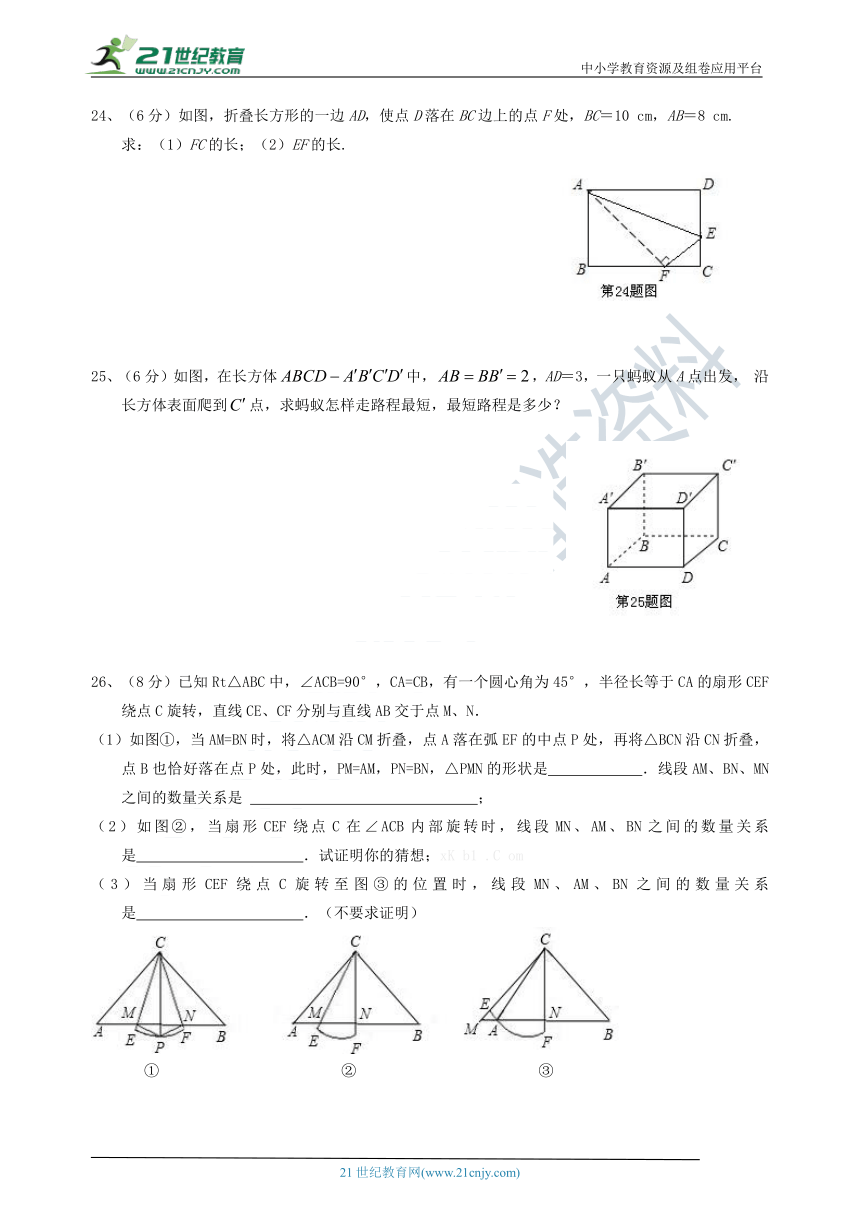
24、(6分)如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10 cm,AB=8 cm.
求:(1)FC的长;(2)EF的长.
25、(6分)如图,在长方体中,,AD=3,一只蚂蚁从A点出发, 沿 长方体表面爬到点,求蚂蚁怎样走路程最短,最短路程是多少?
26、(8分)已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 等腰直角三角形.线段AM、BN、MN之间的数量关系是 MN);
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 AM2+BN2=MN2.试证明你的猜想;xK b1 .C om
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 AM2+BN2=MN2.(不要求证明)
① ② ③
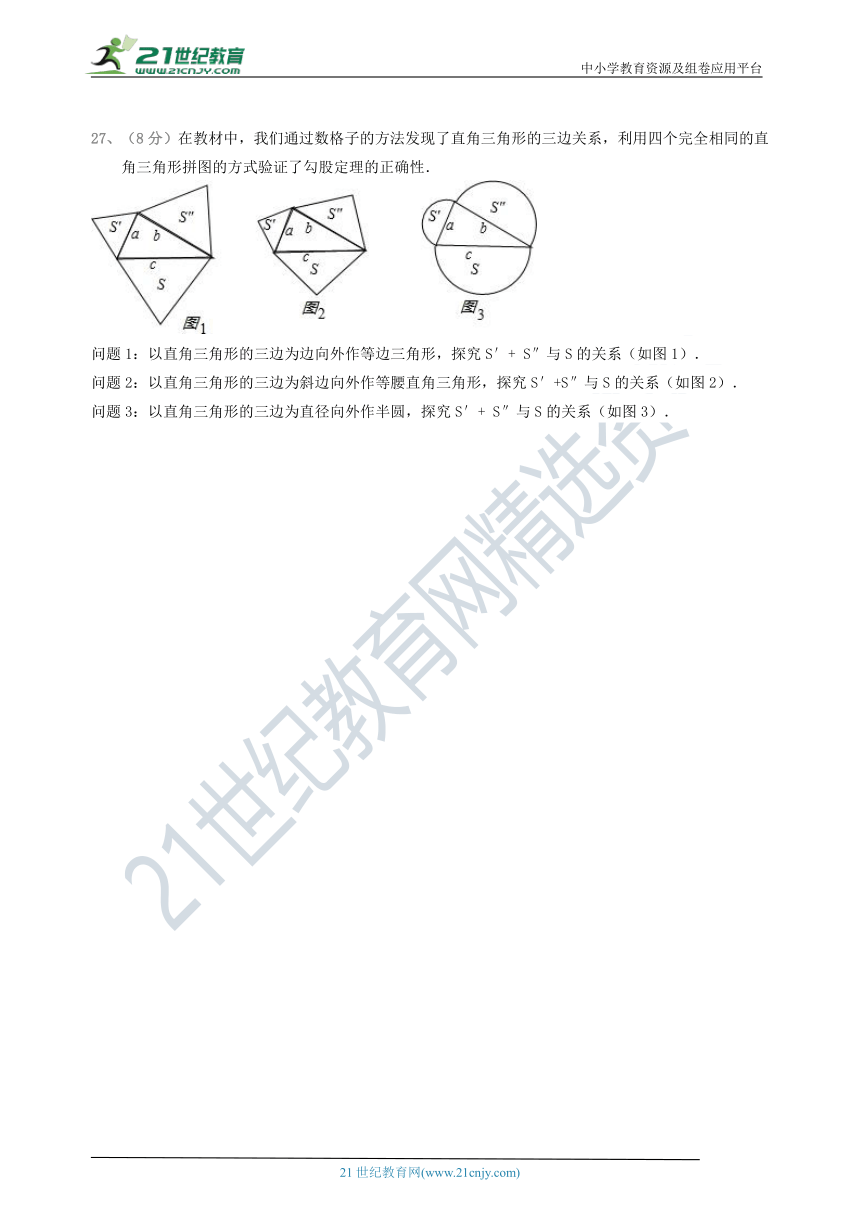
27、(8分)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用四个完全相同的直角三角形拼图的方式验证了勾股定理的正确性.http://w ww.xkb1.com
问题1:以直角三角形的三边为边向外作等边三角形,探究S′+ S″与S的关系(如图1).
问题2:以直角三角形的三边为斜边向外作等腰直角三角形,探究S′+S″与S的关系(如图2).
问题3:以直角三角形的三边为直径向外作半圆,探究S′+ S″与S的关系(如图3).
参考答案
一、选择题
ACADC BBBBA
二、填空题
11、8; 12、直角三角形; 13、直角三角形; 14、612; 15、6; 16、10; 17、66或126.
三、解答题
18、解:∵DF=CD=DG,∴∠DGF=30°.∵∠EKG+∠KGE=90°,∠KGE+∠DGF =90°,
∴∠EKG=∠DGF=30°.∵2∠DKG+∠GKE=180°,∴∠DKG=75°.
19、解:如图,在△ABC中,AB=15,BC=14,AC=13,设,∴ .
由勾股定理,得,
,
∴ ,解得. ∴ .
∴ .
20、解:在Rt△中,由勾股定理,得,即,
解得AC=3,或AC=-3(舍去).因为每天凿隧道0.2 km,
所以凿隧道用的时间为3÷0.2=15(天).
答:15天才能把隧道AC凿通.
21、解:(1)因为三个内角的比是1︰2︰3,所以设三个内角的度数分别为k,2k,3k(k≠0).
由k+2k+3k=180°,得k=30°,
所以三个内角的度数分别为30°,60°,90°.
(2)由(1)知三角形为直角三角形,则一条直角边长为1,斜边长为2.
设另外一条直角边长为x,则,即.所以另外一条边长的平方为3.
22、分析:旗杆折断的部分、未折断的部分和折断后原旗杆顶部离旗杆底部的部分构成了直角三角形,运用勾股定理可将折断的位置求出.
解:设旗杆未折断部分的长为x m,则折断部分的长为(16-x)m,
根据勾股定理,得,解得,即旗杆在离底部6 m处断裂.
23、解:(1)n2-1 2n n2+1
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵ a2+b2=(n2-1)2+4n2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2=c2,
∴ 以a,b,c为边长的三角形是直角三角形.
24、解:(1)由题意,得AF=AD=BC=10 cm,在Rt△ABF中,∠B=90°,∵ cm,
∴ ,BF=6 cm,∴ (cm).
(2)由题意,得,设的长为,则.在Rt△中,∠C=90°,
由勾股定理,得即,解得,即的长为5 cm.
25、解:蚂蚁沿如图(1)所示的路线爬行时,长方形长为,宽为,
连接,则构成直角三角形.
由勾股定理,得.
蚂蚁沿如图(2)所示的路线爬行时,长方形长为,宽为,
连接,则构成直角三角形.
由勾股定理,得,.
蚂蚁沿如图(3)所示的路线爬行时,长方形长为宽为AB=2,连接,则构成直角三角形.
由勾股定理,得
∴ 蚂蚁从点出发穿过到达点时路程最短,最短路程是5.
26、解:(1)根据折叠的性质知:△CAM≌△CPM,△CNB≌△CNP.∴AM=PM,∠A=∠CPM,PN=NB,∠B=∠CPN. ∴∠MPN=∠A+∠B=90°,PM=PN=AM=BN.
故△PMN是等腰直角三角形,AM2+BN2=MN2(或AM=BN=MN).
(2)AM2+BN2=MN2.
证明:如图,将△ACM沿CM折叠,得△DCM,连DN,
则△ACM≌△DCM,∴CD=CA,DM=AM,∠DCM=∠ACM.
同理可知∠DCN=∠BCN,△DCN≌△BCN,DN=BN,
而∠MDC=∠A=45°,∠CDN=∠B=45°,∴∠MDN=90°,
∴DM2+DN2=MN2,故AM2+BN2=MN2.
(3)AM2+BN2=MN2;解法同(2).
27、解:探究1:由等边三角形的性质知:S′=a2,S″=b2,S=c2,
则S′+ S″=(a2+b2).因为a2+b2=c2,所以S′+ S″=S.
探究2:由等腰直角三角形的性质知:S′=a2,S″=b2,S=c2.
则S′+S″=(a2+b2).因为a2+b2=c2,所以S′+S″=S.
探究3:由圆的面积计算公式知:S′=πa2,S″=πb2,S=πc2.
则S′+ S″=π(a2+b2),因为a2+b2=c2,所以S′+ S″=S.X k B 1 . c o m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版八年级数学上册第一章测试卷(含答案)
学校; 班级: 姓名: 评分:
一、选择题(每小题3分,共30分)
1、下列四组数中不能构成直角三角形的一组是 ( )
A.4,5,6 B.7,24,25 C.5,12,13 D.1,2,
2、下列说法中正确的是 ( )
A.已知a,b,c是三角形的三边,则
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△ABC中,∠C=90°,所以
D.在Rt△ABC中,∠B=90°,所以
3、如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,
折痕为MN,则线段CN长是( )
A.3cm B.4cm C.5cm D.6cm
4、如图,已知正方形B的面积为144,如果正方形C的面积为169,那么正方形A的面积为( )
A.313 B.144 C.169 D.25
第3题图
5、如图,在Rt△ABC中,∠ACB=90°,若AC=5 cm,BC=12 cm,则斜边上的高CD的长为( )
A.6 cm B.8.5 cm C.cm D.cm
6、如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的( )
A.1倍 B.2倍 C.3倍 D.4倍
7、在△ABC中,AB=6,AC=8,BC=10,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
8、如果三角形的三边5,m,n满足(m+n)(m-n)=25,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
9、如果一个三角形的三边长a,b,c满足a2+b2+c2+338=10a+24b+26c,那么这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10、在Rt△ABC中,∠C=90°,∠A,∠B,∠C所对的边分别为a,b,c,已知a∶b=3∶4,c=10,则
△ABC的面积为( )
A.24 B.12 C.28 D.30
二、填空题(每小题4分,共28分)
11、在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2= .
12、把一根12厘米长的铁丝,从一端起顺次截下3厘米和5厘米的两根铁丝,用这三条铁丝摆成的三角形是 .
13、已知,则由x,y,z为三边的三角形是 .
14、如图,某会展中心在会展期间准备将高5 m,长13 m,宽2 m的楼道上铺地毯,已知地毯每平方米18元,请你帮助计算一下,铺完这个楼道至少需要________元钱.
第15题图
15、(2015·湖南株洲中考) 如图是“赵爽弦图”,△ABH,△BCG,△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形,如果AB=10,EF=2,那么AH等于 .
16、如题16图,有一圆柱,其高为8cm,它的底面半径2cm,在
下底面点A处有一只蚂蚁,它想得到上底面与点A相对的点
B处的食物,则蚂蚁沿圆柱侧面爬行的最短路程
为 cm(注:π取3).
17、在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,
则△ABC的面积为 cm2 .
三、解答题(共62分)
18、(5分)如图,EF是正方形两对边中点的连线段,将∠A沿DK折叠,使它的顶点A落在EF上的 G点,求∠DKG的度数.
19、(5分)在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
20、(6分)如图,为修铁路需凿通隧道AC,现测量出∠ACB=90°,AB=5 km,BC=4 km,
若每天凿隧道0.2 km,问几天才能把隧道AC凿通?
21、(6分)若三角形的三个内角的比是1︰2︰3,最短边长为1,最长边长为2.
求:(1)这个三角形各内角的度数;
(2)另外一条边长的平方.
22、(6分)如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8 m处,已知旗杆原长16 m,你能求出旗杆在离底部多少米的位置断裂吗?
23、(6分)张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:
a=__________,b=__________,c=__________.
(2)以a,b,c为边长的三角形是不是直角三角形?为什么?
24、(6分)如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10 cm,AB=8 cm.
求:(1)FC的长;(2)EF的长.
25、(6分)如图,在长方体中,,AD=3,一只蚂蚁从A点出发, 沿 长方体表面爬到点,求蚂蚁怎样走路程最短,最短路程是多少?
26、(8分)已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 等腰直角三角形.线段AM、BN、MN之间的数量关系是 MN);
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 AM2+BN2=MN2.试证明你的猜想;xK b1 .C om
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 AM2+BN2=MN2.(不要求证明)
① ② ③
27、(8分)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用四个完全相同的直角三角形拼图的方式验证了勾股定理的正确性.http://w ww.xkb1.com
问题1:以直角三角形的三边为边向外作等边三角形,探究S′+ S″与S的关系(如图1).
问题2:以直角三角形的三边为斜边向外作等腰直角三角形,探究S′+S″与S的关系(如图2).
问题3:以直角三角形的三边为直径向外作半圆,探究S′+ S″与S的关系(如图3).
参考答案
一、选择题
ACADC BBBBA
二、填空题
11、8; 12、直角三角形; 13、直角三角形; 14、612; 15、6; 16、10; 17、66或126.
三、解答题
18、解:∵DF=CD=DG,∴∠DGF=30°.∵∠EKG+∠KGE=90°,∠KGE+∠DGF =90°,
∴∠EKG=∠DGF=30°.∵2∠DKG+∠GKE=180°,∴∠DKG=75°.
19、解:如图,在△ABC中,AB=15,BC=14,AC=13,设,∴ .
由勾股定理,得,
,
∴ ,解得. ∴ .
∴ .
20、解:在Rt△中,由勾股定理,得,即,
解得AC=3,或AC=-3(舍去).因为每天凿隧道0.2 km,
所以凿隧道用的时间为3÷0.2=15(天).
答:15天才能把隧道AC凿通.
21、解:(1)因为三个内角的比是1︰2︰3,所以设三个内角的度数分别为k,2k,3k(k≠0).
由k+2k+3k=180°,得k=30°,
所以三个内角的度数分别为30°,60°,90°.
(2)由(1)知三角形为直角三角形,则一条直角边长为1,斜边长为2.
设另外一条直角边长为x,则,即.所以另外一条边长的平方为3.
22、分析:旗杆折断的部分、未折断的部分和折断后原旗杆顶部离旗杆底部的部分构成了直角三角形,运用勾股定理可将折断的位置求出.
解:设旗杆未折断部分的长为x m,则折断部分的长为(16-x)m,
根据勾股定理,得,解得,即旗杆在离底部6 m处断裂.
23、解:(1)n2-1 2n n2+1
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵ a2+b2=(n2-1)2+4n2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2=c2,
∴ 以a,b,c为边长的三角形是直角三角形.
24、解:(1)由题意,得AF=AD=BC=10 cm,在Rt△ABF中,∠B=90°,∵ cm,
∴ ,BF=6 cm,∴ (cm).
(2)由题意,得,设的长为,则.在Rt△中,∠C=90°,
由勾股定理,得即,解得,即的长为5 cm.
25、解:蚂蚁沿如图(1)所示的路线爬行时,长方形长为,宽为,
连接,则构成直角三角形.
由勾股定理,得.
蚂蚁沿如图(2)所示的路线爬行时,长方形长为,宽为,
连接,则构成直角三角形.
由勾股定理,得,.
蚂蚁沿如图(3)所示的路线爬行时,长方形长为宽为AB=2,连接,则构成直角三角形.
由勾股定理,得
∴ 蚂蚁从点出发穿过到达点时路程最短,最短路程是5.
26、解:(1)根据折叠的性质知:△CAM≌△CPM,△CNB≌△CNP.∴AM=PM,∠A=∠CPM,PN=NB,∠B=∠CPN. ∴∠MPN=∠A+∠B=90°,PM=PN=AM=BN.
故△PMN是等腰直角三角形,AM2+BN2=MN2(或AM=BN=MN).
(2)AM2+BN2=MN2.
证明:如图,将△ACM沿CM折叠,得△DCM,连DN,
则△ACM≌△DCM,∴CD=CA,DM=AM,∠DCM=∠ACM.
同理可知∠DCN=∠BCN,△DCN≌△BCN,DN=BN,
而∠MDC=∠A=45°,∠CDN=∠B=45°,∴∠MDN=90°,
∴DM2+DN2=MN2,故AM2+BN2=MN2.
(3)AM2+BN2=MN2;解法同(2).
27、解:探究1:由等边三角形的性质知:S′=a2,S″=b2,S=c2,
则S′+ S″=(a2+b2).因为a2+b2=c2,所以S′+ S″=S.
探究2:由等腰直角三角形的性质知:S′=a2,S″=b2,S=c2.
则S′+S″=(a2+b2).因为a2+b2=c2,所以S′+S″=S.
探究3:由圆的面积计算公式知:S′=πa2,S″=πb2,S=πc2.
则S′+ S″=π(a2+b2),因为a2+b2=c2,所以S′+ S″=S.X k B 1 . c o m
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
