3.2.1解一元一次方程(合并同类项)
文档属性
| 名称 | 3.2.1解一元一次方程(合并同类项) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-20 12:45:34 | ||
图片预览


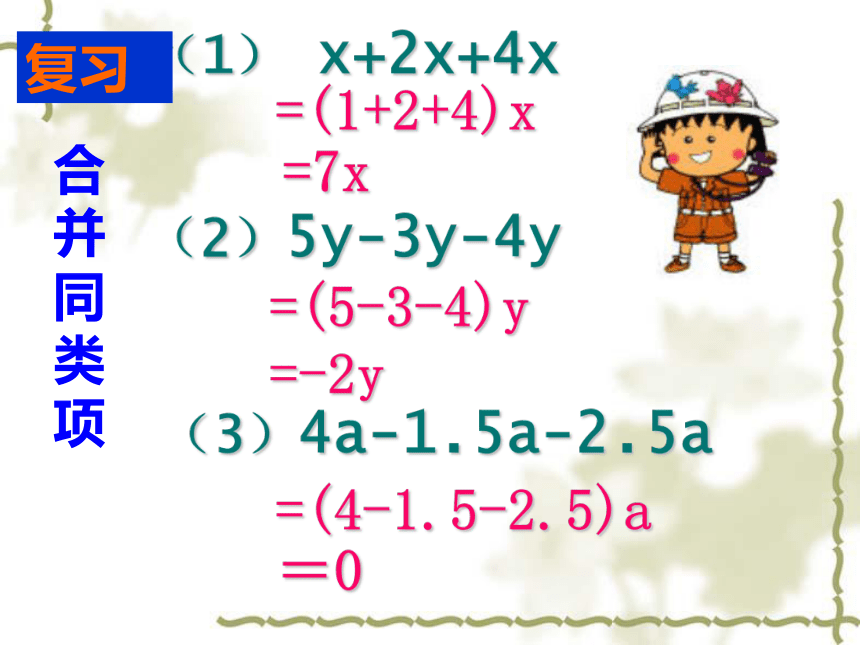



文档简介
课件18张PPT。七年级数学(人教版)上册3.2解一元一次方程(一) ——合并同类项 约公元825年,中亚细亚数学家阿尔—花拉子米写了一本代数书,重点论述怎样解方程。这本书的拉丁译本为《对消与还原》。“对消”与“还原”是什么意思呢? (1) x+2x+4x(2)5y-3y-4y(3)4a-1.5a-2.5a=(1+2+4)x=7x=(5-3-4)y=-2y=(4-1.5-2.5)a合并同类项=0复习实际问题一元一次方程设未知数 列方程 分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法. 请同学记住, 多体会吆!回忆一下:问题1: 某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机?分析: 设前年这个学校购买了计算机x台,则去年购买计算机_____台,今年购买计算机_____台,根据问题中的相等关系:前年购买量+去年购买量+今年购买量=140台
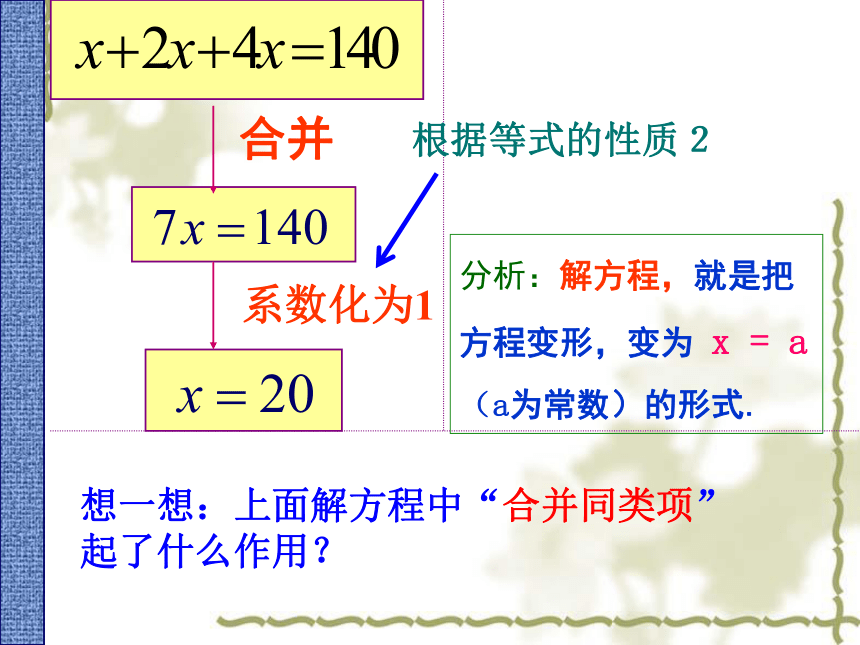
列得方程x + 2x +4x = 1402x4x思考:怎样解这个方程呢?分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.合并系数化为1想一想:上面解方程中“合并同类项”起了什么作用?根据等式的性质2 合并同类项起到了“化简”的作用,即把含有未知数的项合并,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数) .合并同类项的作用:解:合并得系数化为1(合并同类项)(等式性质2)1、2、学会找等量关系列一元一次方程,正确地使用合并的方法解方程。思考:如何列方程?分哪些步骤?一.设未知数:二.分析题意找出等量关系:三.根据等量关系列方程:例1解方程解:合并同类项,得系数化为1,得课堂练习:P 88 练习问题2:
洗衣厂今年计划生产洗衣机25500台,其中Ⅰ型,Ⅱ型,Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台?解:设Ⅰ型 x 台,2x14 x 答: Ⅰ型1500台,Ⅱ型3000台,Ⅲ型21000台。系数化为1,得 x=1500
2x=2×1500=3000 14x=14×1500=21000Ⅱ型 台;Ⅲ型 台,得:合并同类项,得解下列方程你一定会!小试牛刀P89例3一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33。求这个数。解:设这个数是x,得:考考你《对消与还原》 阿尔·花拉米子(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。 “对消”指的就是“合并”,“还原”将在下一节继续学习。
你今天学习的解方程有哪些步骤?小结 合并同类项系数化为1 (等式性质2)
2:如何列方程?分哪些步骤?一.设未知数:二.分析题意找出等量关系:三.根据等量关系列方程:作业:祝同学们学习进步!
列得方程x + 2x +4x = 1402x4x思考:怎样解这个方程呢?分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.合并系数化为1想一想:上面解方程中“合并同类项”起了什么作用?根据等式的性质2 合并同类项起到了“化简”的作用,即把含有未知数的项合并,从而把方程转化为ax=b,使其更接近x=a的形式(其中a,b是常数) .合并同类项的作用:解:合并得系数化为1(合并同类项)(等式性质2)1、2、学会找等量关系列一元一次方程,正确地使用合并的方法解方程。思考:如何列方程?分哪些步骤?一.设未知数:二.分析题意找出等量关系:三.根据等量关系列方程:例1解方程解:合并同类项,得系数化为1,得课堂练习:P 88 练习问题2:
洗衣厂今年计划生产洗衣机25500台,其中Ⅰ型,Ⅱ型,Ⅲ型三种洗衣机的数量之比为1:2:14,这三种洗衣机计划各生产多少台?解:设Ⅰ型 x 台,2x14 x 答: Ⅰ型1500台,Ⅱ型3000台,Ⅲ型21000台。系数化为1,得 x=1500
2x=2×1500=3000 14x=14×1500=21000Ⅱ型 台;Ⅲ型 台,得:合并同类项,得解下列方程你一定会!小试牛刀P89例3一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33。求这个数。解:设这个数是x,得:考考你《对消与还原》 阿尔·花拉米子(约780——约850)中世纪阿拉伯数学家。出生波斯北部城市花拉子模(现属俄罗斯),曾长期生活于巴格达,对天文、地理、历法等方面均有所贡献。它的著作通过后来的拉丁文译本,对欧洲近代科学的诞生产生过积极影响。 “对消”指的就是“合并”,“还原”将在下一节继续学习。
你今天学习的解方程有哪些步骤?小结 合并同类项系数化为1 (等式性质2)
2:如何列方程?分哪些步骤?一.设未知数:二.分析题意找出等量关系:三.根据等量关系列方程:作业:祝同学们学习进步!
