人教版六年级上册数学5.4 扇形 课件 (共14张PPT)
文档属性
| 名称 | 人教版六年级上册数学5.4 扇形 课件 (共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-03 00:00:00 | ||
图片预览


文档简介
(共14张PPT)
第五单元 圆
5.4 扇形
情景引入
折 扇
扇 贝
扇 形 藻
仔细观察——说说这些物体的名字有什么共同点?
初探新知
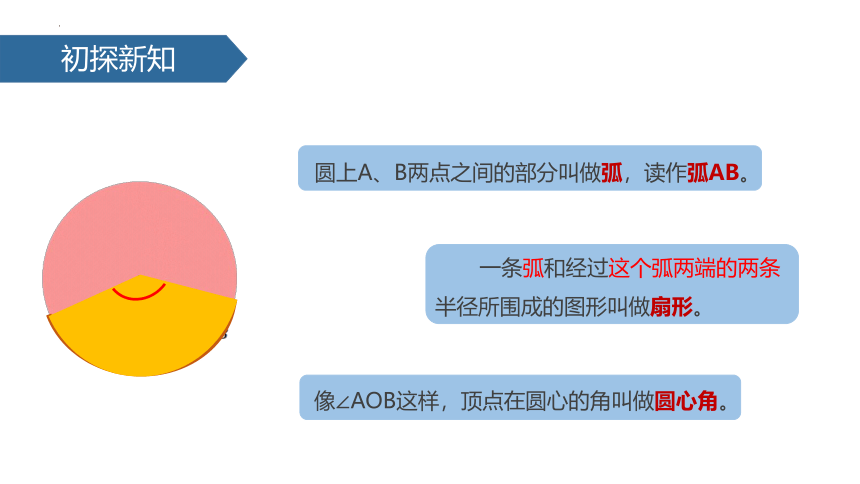
圆上A、B两点之间的部分叫做弧,读作弧AB。
一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。
像∠AOB这样,顶点在圆心的角叫做圆心角。
小试牛刀
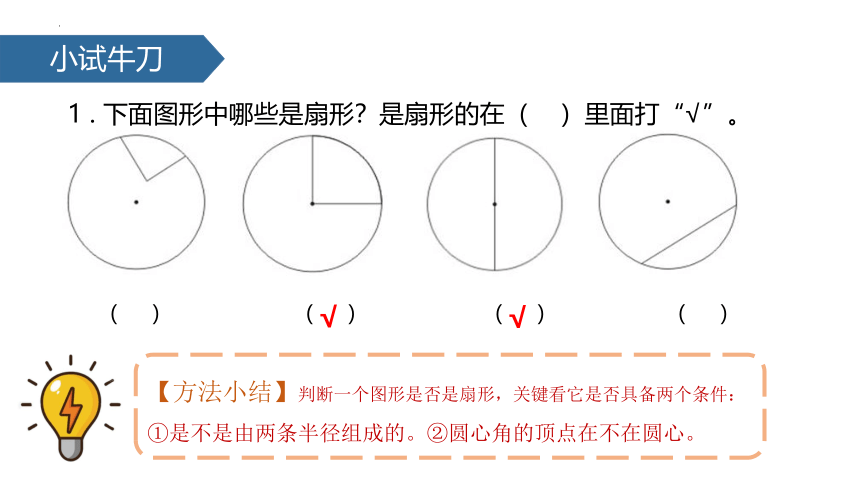
1 . 下面图形中哪些是扇形?是扇形的在( )里面打“√”。
√
( ) ( ) ( ) ( )
√
【方法小结】判断一个图形是否是扇形,关键看它是否具备两个条件: ①是不是由两条半径组成的。②圆心角的顶点在不在圆心。
深入探索
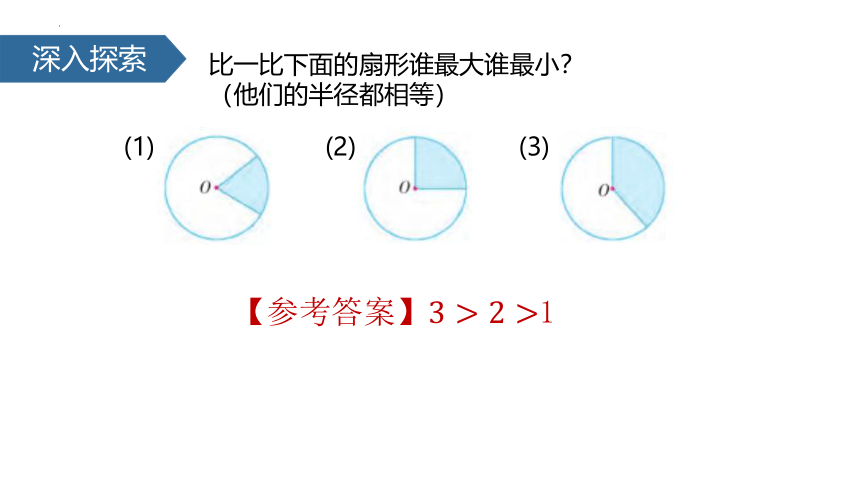
比一比下面的扇形谁最大谁最小?
(他们的半径都相等)
(1)
(2)
(3)
【参考答案】1
深入思考 · 一
问题一:是什么决定了扇形的大小?
扇形的半径和圆心角 。
①半径相同,圆心角越大,扇形越大。
②圆心角相同,半径越大,扇形越大。
问题二:给定扇形的半径和圆心角,你能画出这个扇形吗?要用到什么工具呢?
跟着老师一起探究吧!
应用实践 · 一
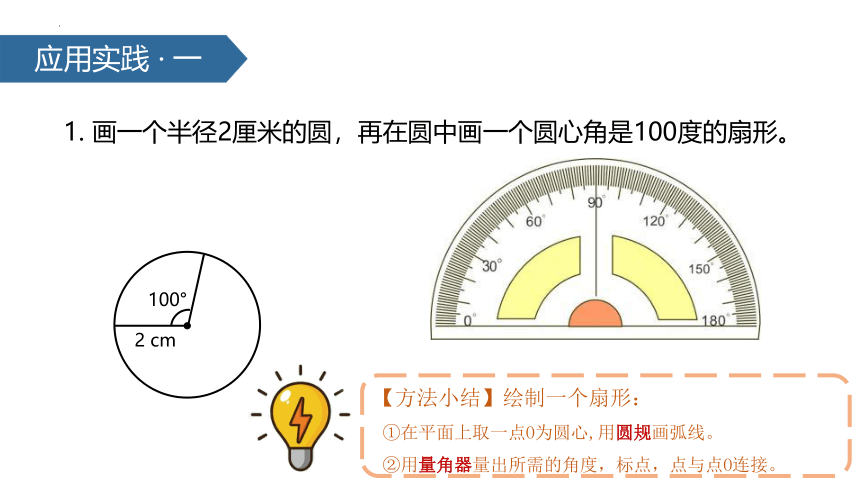
1. 画一个半径2厘米的圆,再在圆中画一个圆心角是100度的扇形。
2 cm
100°
【方法小结】绘制一个扇形:
①在平面上取一点O为圆心,用圆规画弧线。
②用量角器量出所需的角度,标点,点与点O连接。
深入思考 · 二
问题三:什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环 。
问题四:什么是扇环?
一个圆环被截得的部分叫做扇环 。
回想圆环的求法,聪明的你知道如何求扇环的面积吗?
应用实践 · 二
外圆面积:5 =25 (dm )
内圆面积:2 =4 (dm )
圆环面积:25 – 4 = 21 (dm )
扇环面积:21 =5.25 (dm )
(1)
【方法小结】求扇环面积:
①判断该扇形是总圆的几分之几()。
②S圆环=S外圆-S内圆 ③S扇环=S圆环×
知识梳理
4个概念
3种方法
1类思想
①弧:圆上A、B两点之间的部分叫做弧,读作弧AB。
②扇形:一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。
③圆心角:像∠AOB这样,顶点在圆心的角叫做圆心角。
0
A
B
半径
半径
④扇环:一个圆环被截得的部分叫做扇环
①判断一个图形是扇形
②按要求绘制一个扇形
③求扇形的面积
类比推理:由学习圆的方法,类比学习和探究扇形
1.扇形都有一个( ),角的顶点在( )。
2.扇形是由两条半径和( )围成的。
3.扇形中两条半径的夹角叫做( )。
4.扇形的大小与( )和( )有关。
5.同一圆内扇形的大小由( )决定;圆心角越( ),扇形就越大。
趁热打铁
圆心角
圆心
两条半径所夹的弧
圆心角
半径的长短
圆心角
圆心角
大
趁热打铁
6.时钟的分针转动一周形成的图形是( ),分针转动20度形成的图形是( )。
7.扇形圆心角的度数大于( )度小于( )度。
8.用分数表示出上图中扇形是圆的几分之几。
( ) ( ) ( )
趁热打铁
9. 在下列圆中画四个圆心角分别为45°、60°、90°、120°的扇形。
45°
60°
90°
120°
趁热打铁
【解析】由图可判断出此扇环的面积由两个部分组成。均是一个以4dm为外圆半径,1dm为内圆半径的圆环面积的1/4,合在一起就是1/2个圆环。求出圆环面积,就可求出扇环的面积。
外圆面积:4 =16 (dm )
内圆面积:1 = (dm )
圆环面积:16 – = 15 (dm )
扇环面积:15 =7.5 (dm )
10.求阴影部分面积
第五单元 圆
5.4 扇形
情景引入
折 扇
扇 贝
扇 形 藻
仔细观察——说说这些物体的名字有什么共同点?
初探新知
圆上A、B两点之间的部分叫做弧,读作弧AB。
一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。
像∠AOB这样,顶点在圆心的角叫做圆心角。
小试牛刀
1 . 下面图形中哪些是扇形?是扇形的在( )里面打“√”。
√
( ) ( ) ( ) ( )
√
【方法小结】判断一个图形是否是扇形,关键看它是否具备两个条件: ①是不是由两条半径组成的。②圆心角的顶点在不在圆心。
深入探索
比一比下面的扇形谁最大谁最小?
(他们的半径都相等)
(1)
(2)
(3)
【参考答案】1
深入思考 · 一
问题一:是什么决定了扇形的大小?
扇形的半径和圆心角 。
①半径相同,圆心角越大,扇形越大。
②圆心角相同,半径越大,扇形越大。
问题二:给定扇形的半径和圆心角,你能画出这个扇形吗?要用到什么工具呢?
跟着老师一起探究吧!
应用实践 · 一
1. 画一个半径2厘米的圆,再在圆中画一个圆心角是100度的扇形。
2 cm
100°
【方法小结】绘制一个扇形:
①在平面上取一点O为圆心,用圆规画弧线。
②用量角器量出所需的角度,标点,点与点O连接。
深入思考 · 二
问题三:什么是圆环?
两个半径不相等的同心圆,大圆面积比小圆面积多的部分就是圆环 。
问题四:什么是扇环?
一个圆环被截得的部分叫做扇环 。
回想圆环的求法,聪明的你知道如何求扇环的面积吗?
应用实践 · 二
外圆面积:5 =25 (dm )
内圆面积:2 =4 (dm )
圆环面积:25 – 4 = 21 (dm )
扇环面积:21 =5.25 (dm )
(1)
【方法小结】求扇环面积:
①判断该扇形是总圆的几分之几()。
②S圆环=S外圆-S内圆 ③S扇环=S圆环×
知识梳理
4个概念
3种方法
1类思想
①弧:圆上A、B两点之间的部分叫做弧,读作弧AB。
②扇形:一条弧和经过这个弧两端的两条半径所围成的图形叫做扇形。
③圆心角:像∠AOB这样,顶点在圆心的角叫做圆心角。
0
A
B
半径
半径
④扇环:一个圆环被截得的部分叫做扇环
①判断一个图形是扇形
②按要求绘制一个扇形
③求扇形的面积
类比推理:由学习圆的方法,类比学习和探究扇形
1.扇形都有一个( ),角的顶点在( )。
2.扇形是由两条半径和( )围成的。
3.扇形中两条半径的夹角叫做( )。
4.扇形的大小与( )和( )有关。
5.同一圆内扇形的大小由( )决定;圆心角越( ),扇形就越大。
趁热打铁
圆心角
圆心
两条半径所夹的弧
圆心角
半径的长短
圆心角
圆心角
大
趁热打铁
6.时钟的分针转动一周形成的图形是( ),分针转动20度形成的图形是( )。
7.扇形圆心角的度数大于( )度小于( )度。
8.用分数表示出上图中扇形是圆的几分之几。
( ) ( ) ( )
趁热打铁
9. 在下列圆中画四个圆心角分别为45°、60°、90°、120°的扇形。
45°
60°
90°
120°
趁热打铁
【解析】由图可判断出此扇环的面积由两个部分组成。均是一个以4dm为外圆半径,1dm为内圆半径的圆环面积的1/4,合在一起就是1/2个圆环。求出圆环面积,就可求出扇环的面积。
外圆面积:4 =16 (dm )
内圆面积:1 = (dm )
圆环面积:16 – = 15 (dm )
扇环面积:15 =7.5 (dm )
10.求阴影部分面积
