人教A版高中数学必修二 一课一练 6.4.1平面几何中的向量方法 向量在物理中的应用举例 同步练习 (含解析)
文档属性
| 名称 | 人教A版高中数学必修二 一课一练 6.4.1平面几何中的向量方法 向量在物理中的应用举例 同步练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-04 21:04:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
6.4.1平面几何中的向量方法 向量在物理中的应用举例
1.若O是△ABC内一点,++=0,则O为△ABC的( )
A.内心 B.外心
C.垂心 D.重心
2.[2022·湖北黄冈高一期末]一物体在力F的作用下,由点A(10,5)移动到点B(4,2),已知F=(3,-5),则F对该物体所做的功为( )
A.6 B.-6
C.3 D.-3
3.在四边形ABCD中,已知=(4,-2),=(7,4),=(3,6),则四边形ABCD的面积是________.
4.如图,已知正方形ABCD的边长为1,点E是AB边上的动点,求:
(1)·的值;
(2)·的最大值.
5.(多选)[2022·福建泉州高一期中]点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
6.[2022·广东茂名高一期中]已知梯形ABCD中,AD∥BC,∠B=,AB=2,BC=4,AD=1,点P,Q在线段BC上移动,且PQ=1,则·的最小值为( )
A.1 B.
C. D.
7.[2022·山东滨州高一期末]一条东西方向的河流两岸平行,河宽250 m,河水的速度为向东2 km/h.一艘小货船准备从河南岸的码头A处出发,航行到位于河对岸B(AB与河的方向垂直)的正西方向并且与B相距250 m的码头C处卸货.若流水的速度与小货船航行的速度的合速度的大小为6 km/h,则当小货船的航程最短时,小货船航行的速度大小是________km/h.
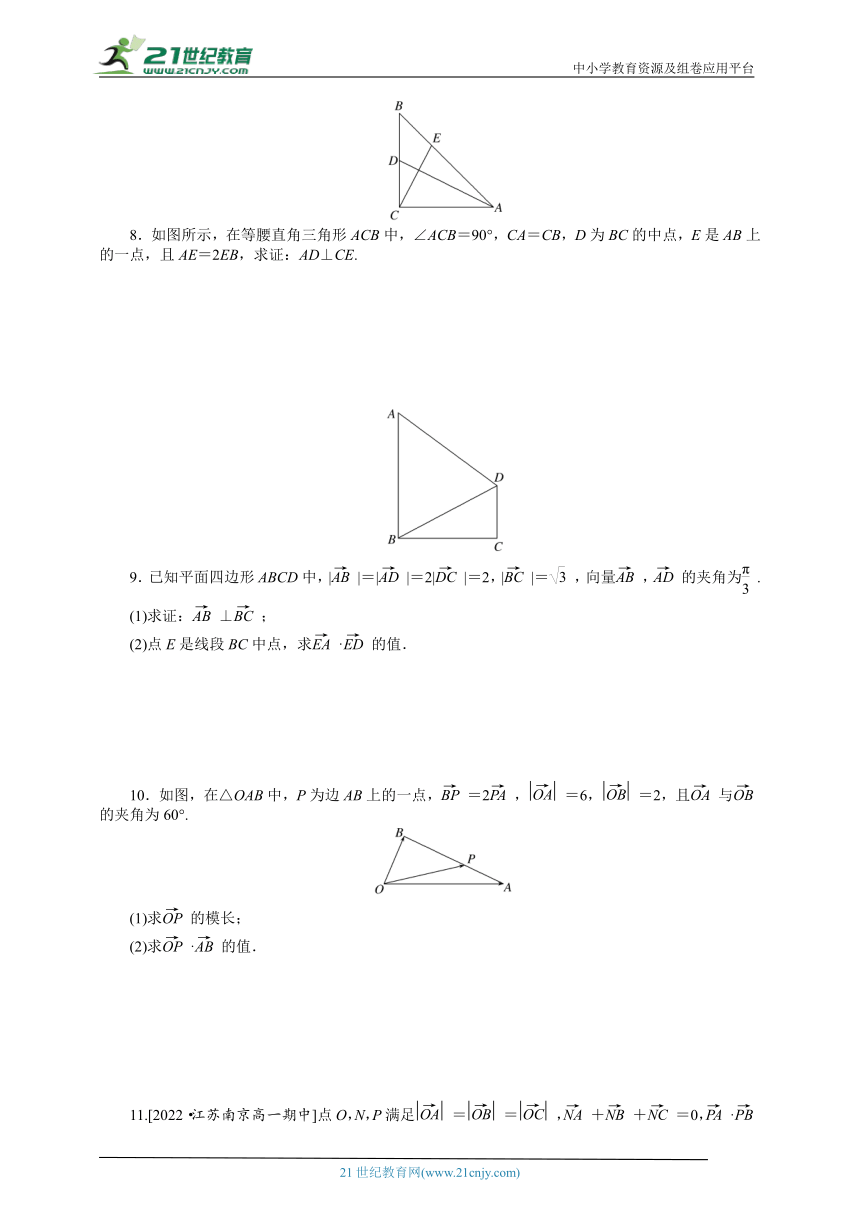
8.如图所示,在等腰直角三角形ACB中,∠ACB=90°,CA=CB,D为BC的中点,E是AB上的一点,且AE=2EB,求证:AD⊥CE.
9.已知平面四边形ABCD中,||=||=2||=2,||=,向量,的夹角为.
(1)求证:⊥;
(2)点E是线段BC中点,求·的值.
10.如图,在△OAB中,P为边AB上的一点,=2,=6,=2,且与的夹角为60°.
(1)求的模长;
(2)求·的值.
11.[2022·江苏南京高一期中]点O,N,P满足==,++=0,·=·=·,则点O,N,P依次是△ABC的( )
A.重心,外心,垂心
B.重心,外心,内心
C.外心,重心,垂心
D.外心,重心,内心
12.[2022·山东菏泽高一期末]如图,在△ABC中,已知AC=1,AB=3,∠BAC=60°,且++=0.求cos ∠APC.
答案:
1.解析:如图,取AB的中点E,连接OE,
则+=2.
又++=0,
所以=-2.又O为公共点,
所以O,C,E三点共线,且||=2||.
所以O为△ABC的重心.故选D.
答案:D
2.解析:由题意得=(-6,-3),所以F对物体做的功W=F·=(3,-5)·(-6,-3)=3×(-6)+(-5)×(-3)=-3.故选D.
答案:D
3.解析:=-=(3,6)=,又因为 ·=(4,-2)·(3,6)=0,
所以四边形ABCD为矩形,所以==2,==3,
所以S=·=2×3=30.
答案:30
4.解析:(1)建立如图所示平面直角坐标系:
则D(0,0),C(0,1),B(1,1),设E(1,x),(0≤x≤1),
所以=(1,x),=(1,0),
所以·=1×1+x×0=1;
(2)因为=(1,x),=(0,1),
所以·=1×0+x×1=x,
因为0≤x≤1,
所以·的最大值是1.
5.解析:∵P是△ABC所在平面内一点,且|-|-|+-2|=0,
∴||-|(-)+(-)|=0,
即||=|+|,
∴|-|=|+|,
两边平方并化简得·=0,
∴⊥,
∴∠A=90°,则△ABC一定是直角三角形,也有可能是等腰直角三角形,
故不可能是钝角三角形,等边三角形,故选AD.
答案:AD
6.
解析:如图,以B为坐标原点,BC所在的直线为x轴建立平面直角坐标系,
因为AD∥BC,∠B=,AB=2,AD=1,
所以D(2,),不妨设P(x,0),Q(x+1,0)(0≤x≤3),
则·=(x-2,-)·(x-1,-)=(x-2)(x-1)+3=x2-3x+5=(x-)2+,
所以当x=时,·取得最小值,故选D.
答案:D
7.解析:由题意,当小货船的航程最短时,航程路线为线段AC,
设小货船航行速度为v,水流的速度为v1,水流的速度与小货船航行的速度的合速度为v2,作出示意图如下:
因为一条东西方向的河流两岸平行,河宽250 m,河水的速度为向正东2 km/h,
AB=250 m,BC=250 m,在Rt△ABC中,有tan ∠BCA===,
所以∠BCA=,∠BAC=,〈v1,v2〉=+=,
所以v=v2-v1,
所以|v|====2,
所以小货船航行速度的大小为2 km/h.
答案:2
8.证明:·=(+)·(+)=(+)·(+)
=(+)·(+-)=(+)·(+)
=-2+2,
因为CA=CB,所以-2+2=0,即·=0,故AD⊥CE.
9.解析:(1)根据题意,画出示意图如下图所示,由题意可知||=||=2,∠BAD= ,所以三角形ABD为等边三角形,则=2,又=1,= ,所以2+2=2,即△BCD为直角三角形,且∠C=,∠B= ,所以∠ABC=+=,所以⊥ ;
(2)根据题意,建立如图所示的平面直角坐标系,则A(0,2),D(,1),因为点E是线段BC中点,所以E, 则=,= ,所以·=·=-+2=.
10.解析:(1)因为=2,所以=+=+=+(-)=+,
因为=6,=2,与的夹角为60°,
所以2=(+)2=2+·+2=×36+×6×2×+×4=,
所以=;
(2)·=(+)·(-)=-2+·+2
=-×36+×6×2×+×4=-.
11.解析:==,则O到三个顶点距离相等,O是△ABC的外心,
++=0,设BC中点为D,则+2=0,N在中线AD上,同理得N在其他两条中线上,故N是△ABC的重心,
·=·,则·(-)=·=0,故PA⊥BC,同理得PB⊥AC,P是△ABC的垂心,故选C.
答案:C
12.解析:由题意得||=3,||=1,,的夹角为∠BAC=60°,
++=0,则+=-,
又=-,=-,所以+=-+-=-3,
故=-(+),同理=(+)=(-+)=(2-),
于是
||2=[-(+)]2=(2+2·+2)=(9+2×3×1×+1)=,
∴||=,
||2=2=(2-4·+42)
=(9-4×3×1×+4)=,∴||=,
∴cos ∠APC=
=
=
===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.4.1平面几何中的向量方法 向量在物理中的应用举例
1.若O是△ABC内一点,++=0,则O为△ABC的( )
A.内心 B.外心
C.垂心 D.重心
2.[2022·湖北黄冈高一期末]一物体在力F的作用下,由点A(10,5)移动到点B(4,2),已知F=(3,-5),则F对该物体所做的功为( )
A.6 B.-6
C.3 D.-3
3.在四边形ABCD中,已知=(4,-2),=(7,4),=(3,6),则四边形ABCD的面积是________.
4.如图,已知正方形ABCD的边长为1,点E是AB边上的动点,求:
(1)·的值;
(2)·的最大值.
5.(多选)[2022·福建泉州高一期中]点P是△ABC所在平面内一点,满足|-|-|+-2|=0,则△ABC的形状不可能是( )
A.钝角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
6.[2022·广东茂名高一期中]已知梯形ABCD中,AD∥BC,∠B=,AB=2,BC=4,AD=1,点P,Q在线段BC上移动,且PQ=1,则·的最小值为( )
A.1 B.
C. D.
7.[2022·山东滨州高一期末]一条东西方向的河流两岸平行,河宽250 m,河水的速度为向东2 km/h.一艘小货船准备从河南岸的码头A处出发,航行到位于河对岸B(AB与河的方向垂直)的正西方向并且与B相距250 m的码头C处卸货.若流水的速度与小货船航行的速度的合速度的大小为6 km/h,则当小货船的航程最短时,小货船航行的速度大小是________km/h.
8.如图所示,在等腰直角三角形ACB中,∠ACB=90°,CA=CB,D为BC的中点,E是AB上的一点,且AE=2EB,求证:AD⊥CE.
9.已知平面四边形ABCD中,||=||=2||=2,||=,向量,的夹角为.
(1)求证:⊥;
(2)点E是线段BC中点,求·的值.
10.如图,在△OAB中,P为边AB上的一点,=2,=6,=2,且与的夹角为60°.
(1)求的模长;
(2)求·的值.
11.[2022·江苏南京高一期中]点O,N,P满足==,++=0,·=·=·,则点O,N,P依次是△ABC的( )
A.重心,外心,垂心
B.重心,外心,内心
C.外心,重心,垂心
D.外心,重心,内心
12.[2022·山东菏泽高一期末]如图,在△ABC中,已知AC=1,AB=3,∠BAC=60°,且++=0.求cos ∠APC.
答案:
1.解析:如图,取AB的中点E,连接OE,
则+=2.
又++=0,
所以=-2.又O为公共点,
所以O,C,E三点共线,且||=2||.
所以O为△ABC的重心.故选D.
答案:D
2.解析:由题意得=(-6,-3),所以F对物体做的功W=F·=(3,-5)·(-6,-3)=3×(-6)+(-5)×(-3)=-3.故选D.
答案:D
3.解析:=-=(3,6)=,又因为 ·=(4,-2)·(3,6)=0,
所以四边形ABCD为矩形,所以==2,==3,
所以S=·=2×3=30.
答案:30
4.解析:(1)建立如图所示平面直角坐标系:
则D(0,0),C(0,1),B(1,1),设E(1,x),(0≤x≤1),
所以=(1,x),=(1,0),
所以·=1×1+x×0=1;
(2)因为=(1,x),=(0,1),
所以·=1×0+x×1=x,
因为0≤x≤1,
所以·的最大值是1.
5.解析:∵P是△ABC所在平面内一点,且|-|-|+-2|=0,
∴||-|(-)+(-)|=0,
即||=|+|,
∴|-|=|+|,
两边平方并化简得·=0,
∴⊥,
∴∠A=90°,则△ABC一定是直角三角形,也有可能是等腰直角三角形,
故不可能是钝角三角形,等边三角形,故选AD.
答案:AD
6.
解析:如图,以B为坐标原点,BC所在的直线为x轴建立平面直角坐标系,
因为AD∥BC,∠B=,AB=2,AD=1,
所以D(2,),不妨设P(x,0),Q(x+1,0)(0≤x≤3),
则·=(x-2,-)·(x-1,-)=(x-2)(x-1)+3=x2-3x+5=(x-)2+,
所以当x=时,·取得最小值,故选D.
答案:D
7.解析:由题意,当小货船的航程最短时,航程路线为线段AC,
设小货船航行速度为v,水流的速度为v1,水流的速度与小货船航行的速度的合速度为v2,作出示意图如下:
因为一条东西方向的河流两岸平行,河宽250 m,河水的速度为向正东2 km/h,
AB=250 m,BC=250 m,在Rt△ABC中,有tan ∠BCA===,
所以∠BCA=,∠BAC=,〈v1,v2〉=+=,
所以v=v2-v1,
所以|v|====2,
所以小货船航行速度的大小为2 km/h.
答案:2
8.证明:·=(+)·(+)=(+)·(+)
=(+)·(+-)=(+)·(+)
=-2+2,
因为CA=CB,所以-2+2=0,即·=0,故AD⊥CE.
9.解析:(1)根据题意,画出示意图如下图所示,由题意可知||=||=2,∠BAD= ,所以三角形ABD为等边三角形,则=2,又=1,= ,所以2+2=2,即△BCD为直角三角形,且∠C=,∠B= ,所以∠ABC=+=,所以⊥ ;
(2)根据题意,建立如图所示的平面直角坐标系,则A(0,2),D(,1),因为点E是线段BC中点,所以E, 则=,= ,所以·=·=-+2=.
10.解析:(1)因为=2,所以=+=+=+(-)=+,
因为=6,=2,与的夹角为60°,
所以2=(+)2=2+·+2=×36+×6×2×+×4=,
所以=;
(2)·=(+)·(-)=-2+·+2
=-×36+×6×2×+×4=-.
11.解析:==,则O到三个顶点距离相等,O是△ABC的外心,
++=0,设BC中点为D,则+2=0,N在中线AD上,同理得N在其他两条中线上,故N是△ABC的重心,
·=·,则·(-)=·=0,故PA⊥BC,同理得PB⊥AC,P是△ABC的垂心,故选C.
答案:C
12.解析:由题意得||=3,||=1,,的夹角为∠BAC=60°,
++=0,则+=-,
又=-,=-,所以+=-+-=-3,
故=-(+),同理=(+)=(-+)=(2-),
于是
||2=[-(+)]2=(2+2·+2)=(9+2×3×1×+1)=,
∴||=,
||2=2=(2-4·+42)
=(9-4×3×1×+4)=,∴||=,
∴cos ∠APC=
=
=
===.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
